Контрольная работа 1 семестр

1. Контрольная работа по теме 1, 1-й семестр

Задание 1. Найдите область определения функции:

1. 2.

3. 4.

5. 6.

7. 8.

9. 10.

11. 12.

13. 14.

15. 16.

17. 18.

19. 20.

Задание 2. Постойте графики функций:

1. а), б); 2. а), б);

3. а) б); 4. а) б);

5. а) б); 6. а), б);

7. а) , б); 8. а) б);

9. а), б); 10. а) б);

11. а) б); 12. а) б);

13. а) , б); 14. а) б);

15. а) б); 16. а) б);

17. а) б) ; 18. а) б) ;

19. а) б); 20. а) б) ;

Задание 3. Определите вид кривой, постройте ее график, найдите, где это возможно, координаты фокусов, значения мнимых и действительных полуосей, уравнения асимптот:

1. х²– 4 у² = 4; 2. х² + 4 у² = 4; 3. 9х² + 4 у² = 36;

4. 9х² – 4 у² = 36; 5. 9х² + 9 у² = 4; 6. х = 4 у² ;

7. 4х² + 16 у² = 64; 8. 4х² – 16 у² = 64; 9. х² + 4 у² = 1;

10. х² – 4 у² = 1; 11. 4х² + 4 у² = 1; 12. 4х² – 4 у² = 1;

13. х = – 4 у²; 14. х = 0,25 у² ; 15. х² + 16 у² = 64;

16. 4х² – у² = 64; 17. х² + 0,25 у² = 1; 18. 0,25х² – 4 у² = 1;

19. 0,04х² + 0,04 у² = 1; 20. 4х² – 4 у² = 9; 21. х²– 16 у² = 4;

Задание 4. Вычислите предел функции:

, где коэффициенты определяются по таблице.

№	a	b	c	d	f	g	h	k	№	a	b	c	d	f	g	h	k
1	0	3	2	1	0	-3	2	4	11	1	2	3	4	-5	6	-7	8
2	-3	2	1	1	-2	2	3	4	12	-2	3	2	4	3	2	-1	0
3	0	4	2	1	-2	3	4	5	13	-1	3	4	6	2	1	2	3
4	2	3	0	3	0	1	2	3	14	-3	4	2	3	-2	3	5	2
5	7	2	3	4	-2	0	1	2	15	4	5	1	9	-2	3	-9	1
6	-7	2	3	4	5	6	7	8	16	0	2	3	1	-2	1	2	2
7	2	-1	0	3	4	0	0	3	17	2	4	4	2	0	2	3	3
8	-9	1	2	3	-3	4	0	0	18	-8	5	5	3	3	3	-3	4
9	0	-1	2	4	0	3	5	8	19	-4	6	6	4	0	4	-4	5
10	0	2	0	3	0	4	0	2	20	-3	7	7	5	-6	5	-6	6

Задание 5. Вычислите предел функции:

1. , 2. , 3. ,

4., 5. , 6. ,

7. , 8. , 9. ,

10. , 11. , 12. ,

13. , 14. , 15. ,

16. , 17. , 18. ,

19. , 20. , 21. ,

Задание 6. Вычислите пределы функций, используя замечательные пределы, где коэффициенты а, b, c, d определяются по таблице задания 4:

а) ; б) .

Задание 7. Найдите производные следующих функций:

Задание 8. Постройте графики функций:

1. ;

2. ;

3. ;

4. ;

5. ;

6. ;

7. ;

8. ;

9. ;

10. ;

11. ;

12. ;

13. 

14. ;

15. 

16. ;

17. ;

18. ;

19. ;

20. ;

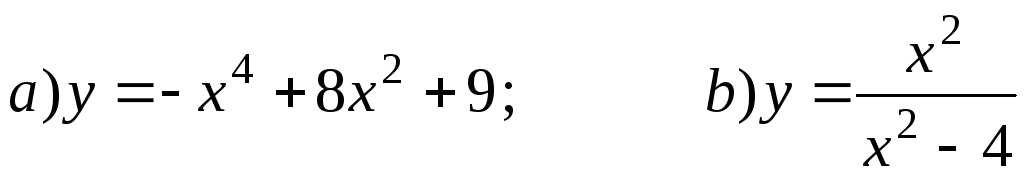Задание 9. Используя исследования, проведенные в задаче 8 а), постройте схематически графики первой и второй производной этих функций.

Задание 10. Для функции из задания 8 а…

1. …напишите уравнение и постройте касательную к графику в точке х = 1 . В какой еще точке графика касательная имеет такой же угловой коэффициент? Напишите ее уравнение и постройте.

2. … вычислите, чему равен тангенс угла наклона касательной к положительному направлению оси 0Х в точке перегиба и точке минимума. Напишите уравнение этих касательных и постройте их.

3. … вычислите, чему равен тангенс угла наклона касательной к положительному направлению оси 0Х в точке перегиба и точке минимума. Напишите уравнение этих касательных и постройте их.

4. …напишите уравнение и постройте касательные к графику в точках с абсциссами х = 0 и х = 1.

5. …определите, в каких точках графика касательная наклонена к положительному направлению оси 0Х под углом 135. Напишите уравнения и постройте эти касательные.

6. …выясните, в каких точках графика тангенс угла наклона касательной к положительному направлению оси 0Х равен 9. Напишите уравнение и постройте эти касательные.

7. … напишите уравнение и постройте касательные к графику в точках с абсциссами х = 2 и х = 2.

8. … напишите уравнение и постройте касательные к графику в точках с абсциссами х = 0,5 и х = 1,5.

9. … определите, в каких точках графика касательная наклонена к положительному направлению оси 0Х под углом 45. Напишите уравнения и постройте эти касательные.

10. … определите, в каких точках графика касательная наклонена к положительному направлению оси 0Х под углом 45. Напишите уравнения и постройте эти касательные.

11. …напишите уравнение и постройте касательные к графику в точках с абсциссами х =1 и х = 1.

12. … напишите уравнение и постройте касательную к графику в точке х = 1. В какой еще точке графика касательная имеет такой же угловой коэффициент? Напишите ее уравнение и постройте.

13. … постройте и напишите уравнения касательных в точках перегиба.

14. … вычислите, чему равен тангенс угла наклона касательной к положительному направлению оси 0Х в точке перегиба и точке минимума. Напишите уравнение этих касательных и постройте их.

15. … напишите уравнение и постройте касательную к графику в точке х = 0 . В какой еще точке графика касательная имеет такой же угловой коэффициент? Напишите ее уравнение и постройте.

16. … напишите уравнение и постройте касательные к графику в точках с абсциссами х = 0 и х = 1.

17. … напишите уравнения касательных и постройте их в точках пересечения графика с осью 0Х.

18. …напишите уравнение и постройте касательные к графику в точках с абсциссами х = 0,5 и х = 0,5.

19. …вычислите, чему равен тангенс угла наклона касательной к положительному направлению оси 0Х в точке перегиба и точке минимума. Напишите уравнение этих касательных и постройте их.

20. …напишите уравнение и постройте касательную к графику в точке х = 0. В какой еще точке графика касательная имеет такой же угловой коэффициент? Напишите ее уравнение и постройте.

Задание 11. Решите задачу:

1. Точка движется прямолинейно согласно заданному закону движения , где S – путь (в м), t – время (в с). Найдите скорость в момент t =2с и ускорение в момент t =3с.

2. Найдите силу, действующую на тело массой 300г. в момент времени t₀ = 1c., если тело движется прямолинейно и его скорость изменяется по закону V = 2t³ + 3, где V м/с - скорость, t_c - время (по второму закону Ньютона F = m × a, где m - масса, а - ускорение).

3. Материальная точка движется прямолинейно по закону (где t[2;5]). Доказать, что сила, действующая на него, пропорциональна кубу пройденного пути (по второму закону Ньютона F = m × a, где m - масса, а - ускорение).

4. Точка движется прямолинейно, согласно заданному закону движения , где S – путь (в м), t – время (в сек). Найдите тот момент времени, когда ускорение равно 0.

5. По прямой линии движутся две точки. Закон движения первой точки задан функцией f(t) = e^t, второй точки g(t) = 5t² + 0,75t + 0,5. Определите, в какие моменты времени точки имеют одинаковое ускорение?

6. Точка движется прямолинейно по закону где S – путь (в м), t – время (в сек). Найдите путь, пройденный точкой до полной остановки.

7. Зависимость пути от времени при прямолинейном движении точки задана уравнением (м). В какой момент времени скорость движения будет наибольшей. Какой путь будет пройден к этому времени?

8. Зависимость пути от времени при прямолинейном движении точки задана уравнением . Найдите максимальную скорость движения этой точки.

9. Точка движется прямолинейно по закону 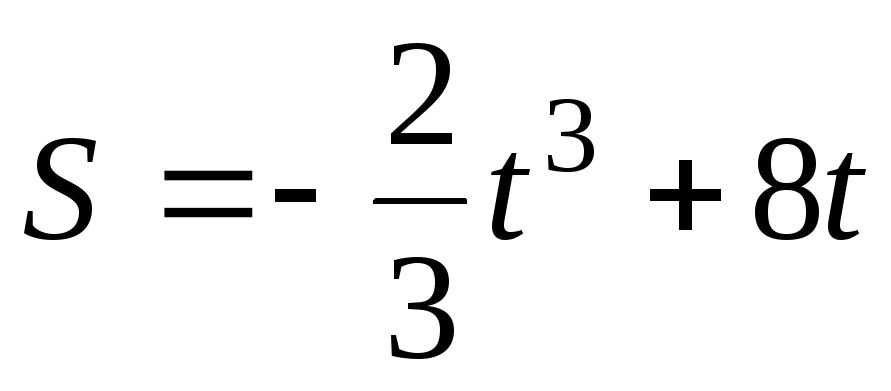, где S – путь (м), t – время (сек). Найдите путь, пройденный точкой до полной остановки.

10. Тело движется прямолинейно по закону , где S – путь (в м), t – время (в сек). В какой момент времени тело остановится?

11. Пуля вылетает из пистолета со скоростью v_o=800 м/c. Найдите скорость пули в момент t =10 с, если она движется по закону (S – путь в м, g =10 м/c²).

12. Зависимость пути от времени при прямолинейном движении точки задана уравнением S = - t³ + 6 t² + 24 t - 5 (м). В какой момент времени скорость была наибольшей. Найдите эту скорость (время в секундах).

13. Зависимость пути от времени при прямолинейном движении точки задана уравнением (м). Какова максимальная скорость движения этой точки?

14. Дано уравнение движения тела S = 3 - 8t + 3,5t². Вывести формулу ускорения тела и постройте график ускорения.

15. Зависимость пути от времени при прямолинейном движении точки задана уравнением . Найдите максимальную скорость движения этой точки, где S (м), t (с).

16. Даны законы прямолинейного движения двух точек (S – путь в м, t – время в сек) S₁ = 2t³ - 5t² - 3t; S₂ = 2t³ + 5t² -11t + 7. Найдите время t, когда скорости этих точек равны.

17. Закон движения зенитного снаряда, выпущенного вертикально вверх, приближенно определяется выражением , где S – путь (в м), t – время (в сек). Найдите начальную скорость движения снаряда.

18. Тело массой m движется по закону под действием силы F. Найдите силу F, действующую на тело, в любой момент времени t в секундах (по второму закону Ньютона F = m × a, где m - масса, а - ускорение). Какой путь пройдет тело к концу второй секунды?

19. Точка движется по закону S(t) = t³ - 2t² + 3 (t - в секундах, S - в метрах). Найдите: а) среднюю скорость за время 2 £ t £ 4 ; б) мгновенную скорость при t₁ = 2c, t₂ = 4c.

20. Тело движется по закону S = t³ + t + 1. Найдите: а) среднюю скорость за время t₁ £ t £ t₂ , если t₁ = 2с, t₂ = 5с; б) мгновенную скорость при t₁ = 2c, t₂ = 5c.

2. Контрольная работа по теме 2, 1-й семестр

Вариант № 1

1. Найдите и нарисуйте на координатной плоскости область определения функции .

2. Найдите все частные производные 1-ого порядка для функции

.

Найдите градиент функции z в точке F (2; 1) и производную по направлению вектора в этой же точке F.

3. Постройте линии уровня для функции .

4. Исследуйте на экстремум функцию .

5. Найдите условный экстремум функции 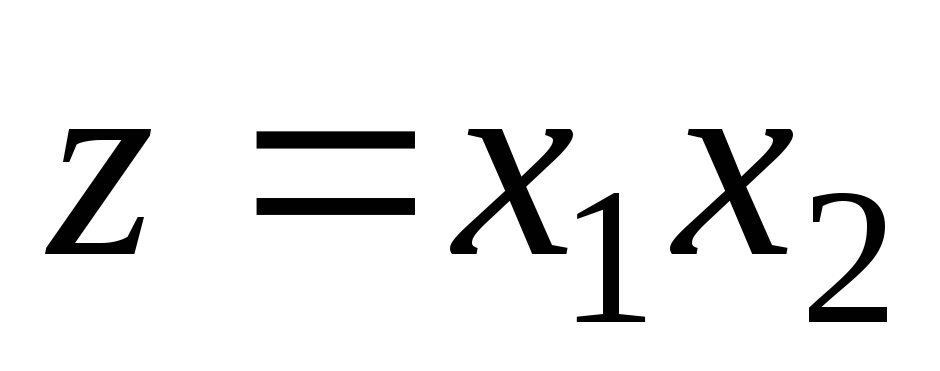при .

6. Определите какой набор товаров выберет потребитель, обладающий доходом в 300д.ед., если его функция полезности , а цены единицы товара р₁ = 2 д.ед., р₂ = 4 д.ед. Напишите уравнения линий безразличия и нарисуйте три из них при различных значениях u .