Тема 6
Метрические задачи. Определение
Расстояния между двумя точками, двумя прямыми. Определение расстояния от точки до плоскости, углов и натурального вида
ФИГУРЫ
Контрольные вопросы
-
Как определить на эпюре расстояние между двумя точками?
-
Как определить расстояние от точки до прямой?
-
Как определить расстояние между параллельными прямыми? между скрещивающимися прямыми?
-
Как определить расстояние от точки до плоскости общего положения?
-
Как определить расстояние между двумя параллельными плоскостями?
-
В каких случаях прямой угол проецируется на плоскость проекций без искажения?
-
Как определить натуральную величину угла между прямой и плоскостью?
-
Как определить натуральную величину угла между плоскостями?
Задания
6.1. Определить расстояние между двумя точками А и В способом прямоугольного треугольника.
X12
A2
B1
A1
B2
6.2. Построить горизонтальную проекцию отрезка прямой АВ длиной 45 мм.
X12
A1
A2
B2
6.3. На прямой m от точки А отложить отрезок АВ длиной 30 мм.
X12
A2
m2
m1
A1
6.4. Определить расстояние между точкой A и прямой m.
m2
X12
A1
A2
m1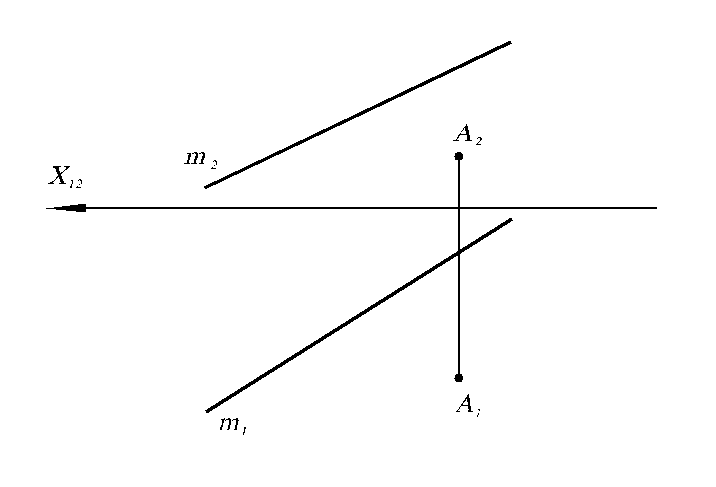
6.5. Из точки К опустить перпендикуляр на прямую AB и определить его величину.
X12
A1
A2
K1
K2
B2
B1
6.6. Построить равнобедренный треугольник АВС с вершиной в точке В и основанием АС, равным 40 мм, на горизонтальной прямой h.
X12
B2
B1
h2
h1
6.7. Построить ромб АВСD по заданным: вершине A, направлению диагонали BD, принадлежащей h, и отношению диагоналей AC BD = 1,5.
X12
A2
A1
h2
h1
6.8. Построить горизонтальную проекцию прямоугольника ABCD.
X12
A2
B2
D2
C2
C1
D1
6.9. От точки A,
принадлежащей плоскости ΔABC,
восстановить перпендикуляр длиной 20
мм. Найти проекции перпендикуляра на
плоскости
и на плоскости
.
X12
A2
A1
B1
C1
C2
B2
6.10. Найти расстояние от точки К до плоскости ΔABC .
X12
A1
A2
K2
B2
C2
C1
B1
K1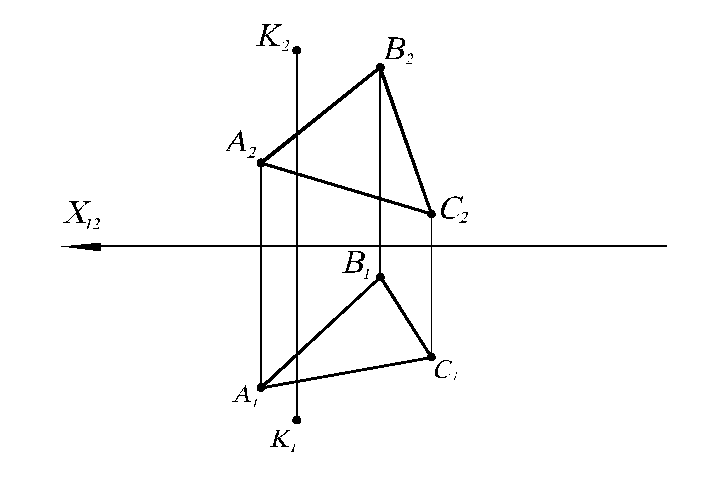
6.11. Найти расстояние от точки К до плоскости T.
Z23
X12
Y13
Y13
K1
K2
T2
T1
0
6.12. Определить расстояние между параллельными прямыми a и b способом плоскопараллельного перемещения.
X12
a2
b2
a1
b1
6.13. Определить расстояние между скрещивающимися прямыми AB и CD.
X12
A2
A1
C2
C1
B2
D2
D1
B1
6.14. Определить расстояние между скрещивающимися прямыми AB и CD.
X12
D1
D2
B2
B1
C2
C1
A2
A2
6.15. Определить расстояние между скрещивающимися прямыми АВ и CD.
C2
B2
X12
A2
A1
C1
D2
D1
B1
6.16. Определить кратчайшее расстояние от точки А до поверхности сферы и построить проекции этого расстояния.
X12
A1
≡
A2
О2
О1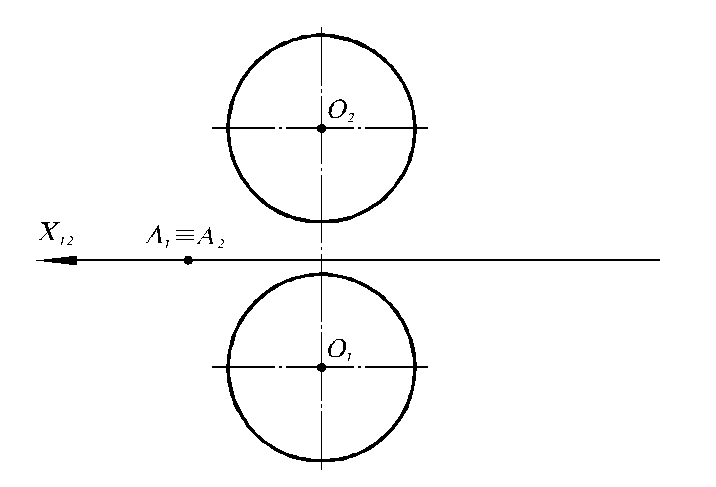
6.17. Определить расстояние от точки М до плоскости Q .
X12
M2
M1
Q2
Q1
Qx
6.18. Определить расстояние между параллельными плоскостями S и P.
S2
X12
S1
Sx
P2
P1
Px
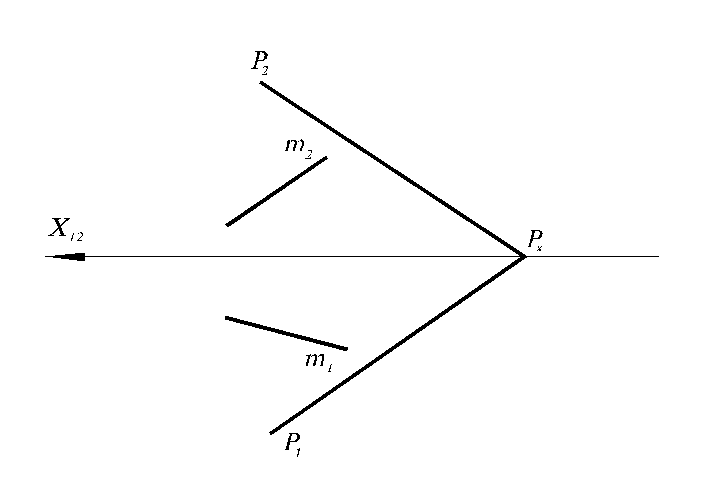
6.19. Построить плоскость P, параллельную плоскости Q (a∩b) и одинаково удаленную от нее и от точки M.
X12
M2
M1
b2
b1
a1
a2
6.20. С помощью линий
наибольшего наклона определить угол
наклона плоскости P
к плоскости
и плоскости ΔABC
к плоскости
.
B2
X12
P2
Px
P1
B1
C2
A2
A1
C1
1
2
6.21. Определить натуральную величину двухгранного угла при ребре ВС. Задачу решить способом замены плоскостей проекций.
A2
C2
B2
D2
B2
D1
B1
C1
A1
X12
6.22. Определить угол между плоскостями G и Q (ΔABC).
X12
G2
Gx
G1
A2
B2
C2
C1
B1
A1
6.23. Определить расстояние от точки К до плоскости G.
X12
A2
A1
G2
Gx
G1
6.24. Определить угол между прямой m и плоскостью P.
X12
P2
Px
m2
m1
P1