Тема 5 способы преобразования проекций

Контрольные вопросы

1. В каком случае геометрические фигуры проецируются в натуральную величину?

2. Перечислите основные методы преобразования проекций, позволяющие осуществить переход от общего положения проецируемой геометрической фигуры к частному, более выгодному.

3. Каким методом преобразования чертежа можно поставить проецируемую плоскость общего положения в положение, перпендикулярное или параллельное одной из плоскостей проекций?

4. В чем заключается сущность плоскопараллельного перемещения?

5. Как будут меняться проекции геометрической фигуры на плоскостях проекций П₁, П₂, П₃, при вращении ее вокруг оси, перпендикулярной горизонтальной плоскости проекции?

6. Как будут выглядеть проекции траектории точки на трех плоскостях проекций вращения точки вокруг горизонтали?

7. В чем состоит сущность способа совмещения?

Задания

5.1. Способом замены плоскостей проекций преобразовать отрезок АВ во фронтально-проецирующий.

A₂

A₁

B₁

B₂

2. Способом замены плоскостей проекций преобразовать отрезок АВ в горизонтально-проецирующий.

A₂

A₁

X₁₂

B₂

B₁

2. Способом замены плоскостей проекций поставить плоскость ΔABC в положение, параллельное горизонтальной плоскости проекции.

X₁₂

A₁

A₁

B₁

B₂

C₂

C₁

2. Способом плоскопараллельного перемещения поставить отрезок АВ в положение, перпендикулярное горизонтальной плоскости проекций.

X₁₂

A₁

A₂

B₁

B₂

2. Способом плоскопараллельного перемещения преобразовать плоскость S во фронтально-проецирующую. Определить проекции отрезка АВ, если AB принадлежит плоскости S.

X₁₂

S₂

S₁

A₂

A₁

S_x

B₁

B₂

2. Вращением вокруг оси, перпендикулярной плоскости проекций, привести отрезок АВ в положение, перпендикулярное горизонтальной плоскости проекций.

X₁₂

A₂

B₂

A₁

B₁

2. Вращением вокруг горизонтали привести плоскость угла (a∩b) в положение, параллельное горизонтальной плоскости проекций. Найти натуральную величину угла.

a₂

X₁₂

b₂

C₂

C₁

a₁

b₁

5.8. Вращением вокруг фронтального следа плоскости S совместить ΔABC, принадлежащий плоскости S, с фронтальной плоскостью проекций.

X₁₂

A₂

B₂

C₂

S₂

S_x

S₁

5.9. Найти горизонтальную проекцию точки A, отстоящей от фронтали f на расстоянии 30 мм.

A₂

f₂

f₁

X₁₂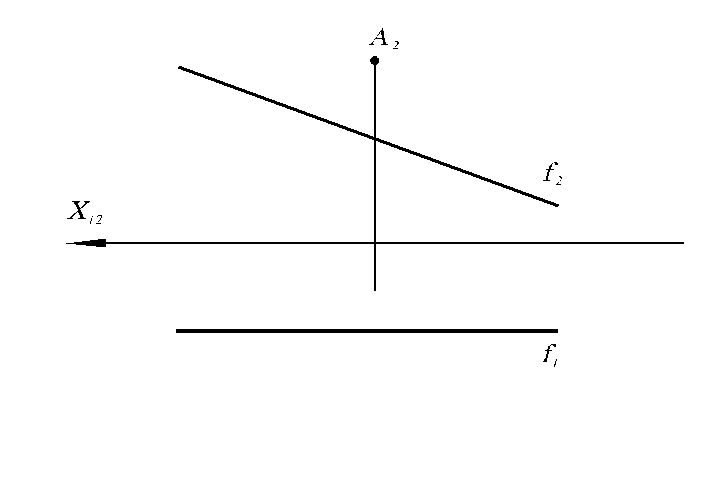

5.10. Построить фронтальную проекцию прямой b, находящейся от прямой a на расстоянии 20 мм.

X₁₂

a₂

a₁

b₁