Тема 3 плоскость

Контрольные вопросы

1. Как можно задать плоскость на чертеже?

2. Что называется следом плоскости?

3. Как располагается в пространстве плоскость общего положения?

4. Какие плоскости называются плоскостями уровня? Назовите их свойства.

5. Какие плоскости называются проецирующими плоскостями? Назовите их свойства.

6. Сколько следов имеют плоскости общего положения? плоскости частного положения?

7. Какие условия определяют принадлежность точки данной плоскости? принадлежность прямой данной плоскости?

8. Какие линии называются главными линиями плоскости? Назовите их основные свойства.

9. Какое условие определяет параллельность прямой и плоскости? параллельность двух плоскостей?

Задания

3.1. Определить положение плоскостей в пространстве.

X₁₂

Q₂

S₂

S_x

G₂

G₁

T₁

S₁

Q_x

Q₁

1 2 3 4

X₁₂

Q₂

Q_x

Q₁

T₂

G₂

G_x

G₁

P₂

P_x

P₁

5 6 7 8

f₂

X₁₂

h₂

f₁

h₁

A₂

B₂

C₂

A₁

A₂

B₁

C₁

B₂

C₂

C₁

B₁

A₁

Q₂

Q_x

Q₁

9 10 11 12

B₂

C₂

A₂

A₁

B₁

C₁

P₂

P_x

P₁

a₂

b₂

a₁ ≡ b₁

m₂ ≡ n₂

m₁

n₁

X₁₂

13 14 15 16

3.2. Точки M и N принадлежат плоскости ΔABC. Определить принадлежность точки К плоскости ΔABC и построить недостающие проекции точек M и N.

B₂

C₂

A₂

X₁₂

A₁

C₁

B₁

K₁

K₂

N₁

M₂

3.3. Найти фронтальную проекцию точки M, принадлежащей плоскости Q.

X₁₂

Q₂

Q₁

Q_x

●

М₁

3.4. Построить следы плоскости, заданной двумя пересекающимися прямыми АВ и CD.

X₁₂

A₂

D₂

B₂

D₁

C₁

B₁

A₁

C₂

3.5. Построить в плоскости ΔABC точку К, удаленную от плоскости на 30 мм, от плоскости - на 25 мм.

B₁

B₂

A₂

A₁

C₁

C₂

X₁₂

3.6. Достроить горизонтальную проекцию треугольника АВС, если известно, что точка М принадлежит плоскости Ρ (ΔABC). В плоскости Ρ провести горизонталь и профильную прямую.

X₁₂

B₂

B₁

C₁

C₂

M₂

M₁

A₂

3.7. Построить фронтальную проекцию прямой m, принадлежащей плоскости Ρ (a||l).

X₁₂

a₂

l₂

a₁

m₁

l₁

8. Заключить отрезок АВ во фронтально-проектирующую плоскость. Построить в этой плоскости горизонталь АС длиной 20 мм и фронталь AD длиной 25 мм.

X₁₂

A₂

B₂

B₁

A₁

3.9. Построить фронтальную проекцию четырехугольника ABCD, принадлежащего плоскости S.

X₁₂

S₂

S_x

S₁

A₁

B₁

C₁

D₁

3.10. Построить фронтальный след плоскости Q. Точка A принадлежит плоскости Q.

X₁₂

A₂

Z₂₃

Y₁₃

Y₁₃

A₁

0

Q₁

Q_y

3.11. Построить горизонтальный след плоскости Ρ. Точка M принадлежит плоскости P.

X₁₂

P₂

M₂

P_x

M₁

3.12. Прямая m принадлежит плоскости. Построить недостающие проекции прямой.

X₁₂

P₂

P_x

P₁

m₁

A₁ ≡ A₂

B₂

m₂

C₂

C₁

B₁

1

2

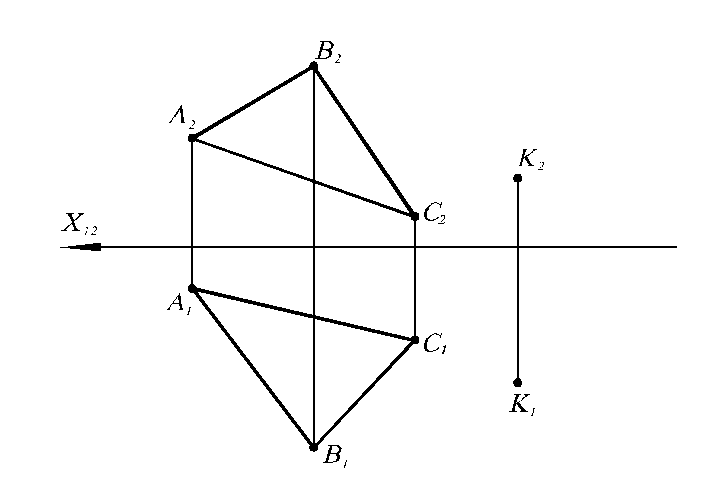
3.13. Через точку К провести горизонтальную прямую длиной 30 мм, параллельную плоскости Q (ΔABC).

B₂

A₂

C₂

K₂

K₁

C₁

A₁

B₁

X₁₂

3.14. Построить недостающие проекции отрезка АВ, параллельного плоскости Δ(m∩n), и отрезка CD, параллельного плоскости S.

S₂

X₁₂

m₂

n₂

A₂

B₂

B₁

m₁

n₁

S_x

C₁

D₁

S₁

3.15. Определить, параллельны ли плоскости.

X₁₂

T₂

T_x

T₁

A₂

B₂

C₂

C₁

B₁

A₁

3.16. Через точку К провести плоскость Q. Прямая m параллельна плоскости Q.

X₁₂

m₂

K₂

Q_x

K₁

m₁

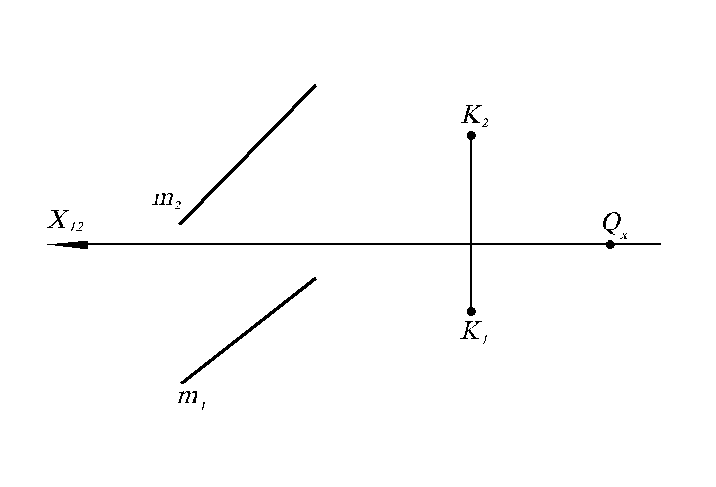
3.17. Через точку К провести плоскость , параллельную плоскости P.

X₁₂

G₂

G_x

K₂

K₁

G₁

3.18. Построить плоскость Δ, параллельную плоскости P, на расстоянии 20 мм.

X₁₂

P_x

P₂

P₁

3.19. Построить плоскость Р, параллельную прямой m.

X₁₂

P₂

P_x

m₂

m₁

3.20. Определить, параллельна ли данная плоскость Q (p∩f) прямой k.

X₁₂

P₂

k₂

f₂

f₁

k₁

P₁