Применение I начала к изопроцессам

1.Изотермический процесс: T=const (рисунок 1)

d'Q=dU+d’A; dT=0, dU=0, следовательно d'Q=d’A. То есть, подведённая теплота полностью тратится на совершение работы, а совершаемая над газом работа выделяется в виде теплоты. Таким образом, должен быть идеальный теплообмен.

Рис. 1 Рис. 2 Рис. 3

Работа при изотермическом процессе:

d’A=PdV, ,, ,

или , Для 1 моля: , .

2.Изохорный процесс: V=const (рисунок 3)

dV=0, d’A=0,d’Q=dU.

Вся подведённая теплота идёт на увеличение внутренней энергии газа .

, . Для 1 моля:

3.Изобарный процесс: P=const (рисунок 2)

d'Q=dU+d’A, Для 1 моля: d'Q= СvdT +PdV, d’Q идёт на увеличение внутренней энергии и работу.

.

Итак:

.Для 1 моля газа: .

Адиабатный процесс

Адиабатическим изменением состояния системы называется такое изменение, которое протекает без обмена теплом между системой и окружающими телами.

Для этого систему нужно окружить абсолютно нетеплопроводными стенками, но так как в реальности таких стенок нет, то всякий реальный адиабатный процесс - приближённый. Близки к адиабатным процессы, протекающие настолько быстро , что обмен с окружающими телами не успевает осуществиться.

Запишем I начало термодинамики: d'Q=dU+d'A, d'Q=0, dU+d'A=0 или

d'A=- dU.

Таким образом, при адиабатном процессе работа системой может совершаться лишь за счёт убыли её внутренней энергии. Если работа совершается над системой – её внутренняя энергия возрастает.

Рассмотрим процесс адиабатного расширения идеального газа.

Для 1 моля газа: , ; =СvdT. Тогда I начало термодинамики примет вид: или .

При адиабатном расширении >0 и dT<0: газ охлаждается.

При адиабатном сжатии <0 и dT>0: газ нагревается.

Таким образом, при адиабатном изменении объёма газа его температура изменяется.

Выведем уравнение адиабатного процесса. Для этого воспользуемся I началом термодинамики и уравнением Менделеева – Клапейрона. Для 1 моля газа:

, Делим почленно:

, интегрируем: ,

, , ,

, , ,

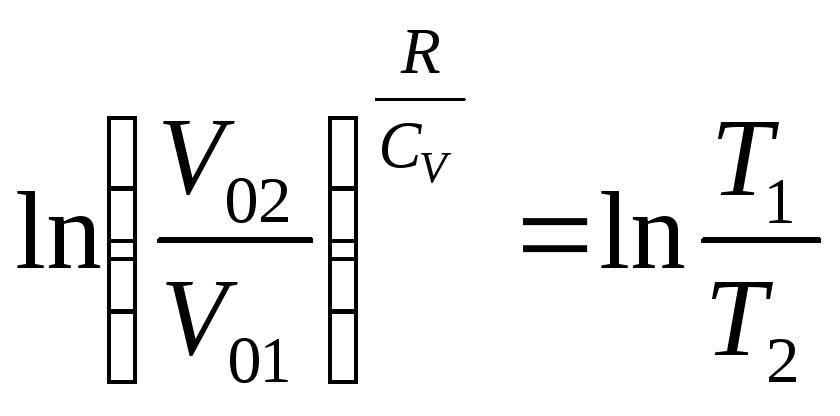, (1) Для произвольной массы газа: (2)

Преобразуем (1) с помощью уравнения Менделеева – Клапейрона:

после деления:(3).

Подставим (3) в(1), получим:

.

- уравнение Пуассона (4) .

Кроме (2) и (4) уравнения адиабатного процесса можно записать в виде: (5).

Работа при адиабатном процессе:

, .

Но , тогда: . Для произвольной массы газа: . Это выражение можно преобразовать к виду: , .

Из уравнения Пуассона следует, что при адиабатном изменении объема газ не подчиняется закону Бойля - Мариотта. Адиабата круче изотермы (Рис. 4).

Рис. 4

Политропический процесс

Политропные (политропические) процессы (ПП)- это такие процессы, при которых теплоёмкость системы остаётся постоянной: C=const.

; при V=const → , при P=const →, при Т=const () , при адиабатном процессе () = 0.

Выведем уравнение политропы для идеального газа.

(1), где - молярная теплоёмкость при политропном процессе.

Для 1 моля газа:

, (2)

Из (2): , (3) обозначим (4)

Тогда(5).

Интегрируем (3), учтём (5) .Получим:; Для произвольной массы газа: (6) – это уравнение политропы (политропного процесса).

Используя уравнение Менделеева – Клапейрона, из (6) получаем уравнение политропы в ином виде:

(7) , (8).

Используя (4) , получаем:

при изотермическом процессе: , тогда n=1 и из (6) имеем: Т=const.

Для адиабатного процесса: , тогда и из (6)имеем: . Для реального процесса:1<<.

Изобарный процесс: , следовательно .

Изохорный процесс: , следовательно . (Из того что).

Работа при политропном процессе определяется формулами для адиабатного процесса при замене .