1.11. Вес и невесомость

Силу тяжести   с которой тела притягиваются к Земле, нужно отличать от веса тела. Понятие веса широко используется в повседневной жизни.

Весом тела называют силу, с которой тело вследствие его притяжения к Земле действует на опору или подвес. При этом предполагается, что тело неподвижно относительно опоры или подвеса. Пусть тело лежит на неподвижном относительно Земли горизонтальном столе (рис. 1.11.1). Систему отсчета, связанную с Землей, будем считать инерциальной. На тело действуют сила тяжести направленная вертикально вниз, и сила упругости с которой опора действует на тело. Силу называют силой нормального давления или силой реакции опоры. Силы, действующие на тело, уравновешивают друг друга: В соответствии с третьим законом Ньютона тело действует на опору с некоторой силой равной по модулю силе реакции опоры и направленной в противоположную сторону: По определению, сила и называется весом тела. Из приведенных выше соотношений видно, что то есть вес тела равен силе тяжести Но эти силы приложены к разным телам!

1

Рисунок 1.11.1. Вес тела и сила тяжести. – сила тяжести, – сила реакции опоры, – сила давления тела на опору (вес тела).

Если тело неподвижно висит на пружине, то роль силы реакции опоры (подвеса) играет упругая силы пружины. По растяжению пружины можно определить вес тела и равную ему силу притяжения тела Землей. Для определения веса тела можно использовать также рычажные весы, сравнивая вес данного тела с весом гирь на равноплечем рычаге. Приводя в равновесие рычажные весы путем уравнивая веса тела суммарным весом гирь, мы одновременно достигаем равенства массы тела суммарной массе гирь, независимо от значения ускорения свободного падения в данной точке земной поверхности. Например, при подъеме в горы на высоту 1 км показания пружинных весов изменяются на 0,0003 от своего значения на уровне моря. При этом равновесие рычажных весов сохраняется. Поэтому рычажные весы являются прибором для определения массы тела путем сравнения с массой гирь (эталонов).

Рассмотрим теперь случай, когда тело лежит на опоре (или подвешено на пружине) в кабине лифта, движущейся с некоторым ускорением относительно Земли. Система отсчета, связанная с лифтом, не является инерциальной. На тело по-прежнему действуют сила тяжести и сила реакции опоры но теперь эти силы не уравновешивают друг друга. По второму закону Ньютона

 

Сила действующая на опору со стороны тела, которую и называют весом тела, по третьему закону Ньютона равна   Следовательно, вес тела в ускоренно движущемся лифте есть

 

Пусть вектор ускорения направлен по вертикали (вниз или вверх). Если координатную ось OY направить вертикально вниз, то векторное уравнение для можно переписать в скалярной форме:

P = m(g – a).

(*)

 

В этой формуле величины P, g и a следует рассматривать как проекции векторов , и на ось OY. Так как эта ось направлена вертикально вниз, g = const > 0, а величины P и a могут быть как положительными, так и отрицательными. Пусть, для определенности, вектор ускорения направлен вертикально вниз, тогда a > 0 (рис. 1.11.2).

2

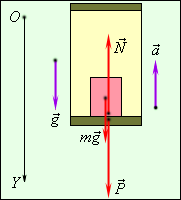
Рисунок 1.11.2. Вес тела в ускоренно движущемся лифте. Вектор ускорения направлен вертикально вниз. 1) a < g, P < mg; 2) a = g, P = 0 (невесомость); 3) a > g, P < 0.

Из формулы (*) видно, что если a < g, то вес тела P в ускоренно движущемся лифте меньше силы тяжести. Если a > g, то вес тела изменяет знак. Это означает, что тело прижимается не к полу, а к потолку кабины лифта («отрицательный» вес). Наконец, если a = g, то P = 0. Тело свободно падает на Землю вместе с кабиной. Такое состояние называется невесомостью. Оно возникает, например, в кабине космического корабля при его движении по орбите с выключенными реактивными двигателями.

Если вектор ускорения направлен вертикально вверх (рис. 1.11.3), то a < 0 и, следовательно, вес тела всегда будет превышать по модулю силу тяжести. Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называют перегрузкой. Действие перегрузки испытывают космонавты, как при взлете космической ракеты, так и на участке торможения при входе корабля в плотные слои атмосферы. Большие перегрузки испытывают летчики при выполнении фигур высшего пилотажа, особенно на сверхзвуковых самолетах.

3

Рисунок 1.11.3. Вес тела в ускоренно движущемся лифте. Вектор ускорения направлен вертикально вверх. Вес тела приблизительно в два раза превышает по модулю силу тяжести (двукратная перегрузка).