Добавил:

student_tipo Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балаковский институт техники, технологии и управления

Предмет:

Системное программное обеспечение

Файл:

ssw_cw

.pdf

Скачиваний:

Добавлен:

11.02.2014

Размер:

910.81 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Разработка компонентов транслятора

_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Решением для Х2 будет:

Х2 = β2α2* = (("-" + "+" + λ)"."(0 + 1) + Х3".")(0 + 1)* = ("-" + "+" + λ)"."(0 + 1)(0 + 1)* + Х3"."(0 + 1)*

Подставим его в другие уравнения. Получаем:

ХЗ = ("-" + "+" + λ)(0 + 1) + Х3(0 + 1)

Х4 = ("-" + "+" + λ)"."(0 + 1)(0 + 1)* + X3"."(0 + 1)* + Х3

Шаг 3. i := i + 1 = 3. Возвращаемся к шагу 2.

Шаг 2. Имеем i = 3 < 4. Берем уравнение для i = 3. Имеем Х3 = ("-" + "+" + λ) (0 + 1) + Х3(0 + 1).

Преобразуем уравнение к виду Х3 = Х3(0 + 1) + ("-" + "+" + λ)(0 + 1).

Тогда

α3 = (0 + 1).

β3 = ("-" + "+" + λ)(0 + 1).

Решением для Х3 будет:

Х3 = β3α3* = ("-" + "+" + λ) (0 + 1)(0 + 1)*.

Подставим его в другие уравнения. Получаем:

Х4 = ("-" + "+" + λ)"."(0 + 1)(0 + 1)* + ("-" + "+" + λ)(0 + 1) (0 + l)*"."α* + ("-" + "+" + λ)(0 + 1)(0 + 1)*.

ШагЗ. i := i + 1 = 4. Возвращаемся к шагу 2. Шаг 2. Имеем i=4 = 4. Переходим к шагу 4. Шаг 4. Уравнение для Х4 теперь имеет вид

Х4 = ("-" + "+" + λ)"."(0 + 1)(0 + 1)* + ("-" + "+" + λ)(0 + 1) (0 + 1)*"."(0 + 1)* + ("-" + "+" + λ)(0 + 1)(0 + 1)*.

Оно не нуждается в преобразованиях и содержит окончательное решение для Х4. Переходим к шагу 5.

Шаг 5. i := i - 1 = 3 > 0. Переходим к шагу 6. Шаг 6. Уравнение для Х3 имеет вид

Х3 = ("-" + "+" + λ) (0 + 1)(0 + 1)*.

Оно уже содержит окончательное решение для Х3. Переходим к шагу 5. Шаг 5. i := i - 1 = 2 > 0. Переходим к шагу 6.

Шаг 6. Уравнение для Х2 имеет вид Х2 = ("-" + "+" + λ)"."αα* + ХЗ"."α*.

Подставим в него окончательное решение для Х3. Получим окончательное решение для Х2:

Х2 = ("-" + "+" + λ)"."(0 + 1)(0 + 1)* + ("-" + "+" + λ)(0 + 1) (0 + 1)*"."(0 + 1)*.

Переходим к шагу 5.

Шаг 5. i := i - 1 = 1 > 0. Переходим к шагу 6. Шаг 6. Уравнение для X1 имеет вид

X1 = ("-" + "+" + λ).

Оно уже содержит окончательное решение для X1. Переходим к шагу 5.

Шаг 5. i := i- 1 = 0 = 0

Алгоритм завершен.

В итоге получили решение: X1 = ("-" + "+" + λ).

Х2 = ("-" + "+" + λ)"."(0 + 1)(0 + 1)* + ("-" + "+" + λ)(0 + 1)(0 + 1)*"."(0 + 1)*. Х3 = ("-" + "+" + λ) (0 + 1)(0 + 1)*.

Х4 = ("-" + "+" + λ)"."(0 + 1)(0 + 1)* + ("-" + "+" + λ)(0 + 1)(0 + 1)*"."(0 + 1)* + ("-" + "+" + λ)(0 + 1)(0 + 1)*.

Выполнив несложные преобразования, это же решение можно представить в более простом

виде:

X1 = ("-" + "+" + λ)

М.Ф.Степанов

Системное программное обеспечение

Х2 = ("-" + "+" + λ)("."(0 + 1) + (0 + 1)(0 + 1)*".")(0 + 1)* Х3 = ("-" + "+" + λ)(0 + 1)*

Х4 = ("-" + "+" + λ)("."(0 + 1) + (0 + 1)(0 + 1)*"." + (0 + 1))(0 + 1)*

Можно заметить, что регулярное выражение для Х4 описывает язык двоичных чисел с плавающей точкой.

Построение лексических анализаторов

Три различных способа, с помощью которых можно задавать регулярные языки:

•регулярные (праволинейные и леволинейные) грамматики;

•конечные автоматы (КА);

•регулярные множества (равно как и обозначающие их регулярные выражения).

Регулярные языки, в принципе, можно определять и другими способами, но именно три указанных способа представляют наибольший интерес.

Для этих трех способов определения регулярных языков можно записать следующие строгие утверждения.

Утверждение 1. Язык является регулярным множеством тогда и только тогда, когда он задан леволинейной (праволинейной) грамматикой.

Утверждение 2. Язык может быть задан леволинейной (праволинейной) грамматикой тогда и только тогда, когда он является регулярным множеством.

Утверждение 3. Язык является регулярным множеством тогда и только тогда, когда он задан с помощью конечного автомата.

Утверждение 4. Язык распознается с помощью конечного автомата тогда и только тогда, когда он является регулярным множеством.

Все три способа определения регулярных языков равноправны. Существуют алгоритмы, которые позволяют для регулярного языка, заданного одним из указанных способов, построить другой способ, определяющий тот же самый язык. Это не всегда справедливо для других способов, которыми можно определить регулярные языки [4, т. 1, 9, 15, 19, 28].

Из всех возможных преобразований практический интерес представляют два преобразования:

•построение регулярного выражения, задающего язык, на основе регулярной грамматики;

•построение КА на основе регулярной грамматики.

Построение регулярного выражения для языка, заданного леволинейной

грамматикой

Для любого регулярного языка, заданного регулярной грамматикой, можно получить регулярное выражение, определяющее тот же язык.

Задача формулируется следующим образом:

•имеется леволинейная грамматика G(VT,VN,P,S),

•необходимо найти регулярное выражение над алфавитом VT, определяющее язык L(G), заданный этой грамматикой.

Задача решается в два этапа:

1.На основе грамматики G, задающей язык L(G), строим систему уравнений с регулярными коэффициентами.

2.Решаем полученную систему уравнений. Решение, полученное для целевого символа грамматики S, будет представлять собой искомое регулярное выражение, определяющее язык L(G).

Поскольку алгоритм решения системы уравнений с регулярными коэффициентами известен,

то далее будет рассмотрен только алгоритм, позволяющий на основе грамматики G(VT,VN,P,S) построить систему уравнений с регулярными коэффициентами.

Построение системы уравнений с регулярными коэффициентами на основе регулярной грамматики

В данном случае, преобразование не столь элементарно. Выполняется оно следующим образом:

1. Обозначим символы алфавита нетерминальных символов VN следующим образом: VN =

22	М.Ф.Степанов

Разработка компонентов транслятора

{X1, Х2,..., Хn}.

Тогда все правила грамматики будут иметь вид:

Xi→Xjγ или Xi→γXj , Xj VN, γ VT*;

Целевому символу грамматики S будет соответствовать некоторое обозначение Xk.

2. Построим систему уравнений с регулярными коэффициентами на основе переменных X1,

Х2,..., Хn:

X1=α01+X1α11+X2α21+ … +Xnαn1

X2=α02+X1α12+X2α22+ … +Xnαn2

…

Xn=α0n+X1α1n+X2α2n+ … +Xnαnn

Коэффициенты α01, α02, … , α0n выбираются следующим образом:

¾α01 = (γ1+γ2+…+γm) , если во множестве правил Р грамматики G существуют правила

Xi→γ1|γ2|…|γm

¾α01 = , если правил такого вида не существует.

Коэффициенты αj1, αj2, … , αjn для некоторого j выбираются следующим образом:

¾αj1 = (γ1+γ2+…+γm) , если во множестве правил Р грамматики G существуют правила Xi→

Xjγ1| Xjγ2|…| Xjγm

¾αj1 = , если правил такого вида не существует.

3. Находим решение построенной системы уравнений.

Доказано, что решение для Xk, которое обозначает целевой символ S грамматики G, будет представлять собой искомое регулярное выражение, обозначающее язык, заданный грамматикой G.

Остальные решения системы будут представлять собой регулярные выражения, обозначающие понятия грамматики, соответствующие ее нетерминальным символам.

В принципе, для поиска регулярного выражения, обозначающего язык, заданный грамматикой, не нужно искать все решения — достаточно найти решение для Xk.

Пример построения регулярного выражения для языка, заданного леволинейной грамматикой

Например, рассмотрим леволинейную грамматику, определяющую язык двоичных чисел с плавающей точкой

G ( {"." , "-" , "+" , "0" , "1"}, {<знак> , <дробное> , <целое> , <число>}, Р , <число>)

Р: <знак> → - | + | λ

Обозначим символы множества VN = {<знак> , <дробное> , <целое> , <число>} соответствующими переменными Хi, получим:

VN = {X1, Х2, Х3, Х4}.

Построим систему уравнений на основе правил грамматики G:

X1 = ("-" + "+" + λ)

Х2 = X1"."(0+1) + Х3"." + Х2(0+1)

Х3 = Х1(0+1) + Х3(0+1)

Х4 = Х2 + Х3 Эта система уравнений уже была решена выше. В данном случае нас интересует только

решение для Х4, которое соответствует целевому символу грамматики G <число>. Решение для Х4 может быть записано в виде:

Х4 = ("-" + "+" + λ)("."(0+1)+ (0+1) (0+1)*"."+ (0+1)) (0+1)*, то есть <число> = ("-" + "+" + λ)("."(0+1)+ (0+1) (0+1)*"."+ (0+1)) (0+1)*.

Это и есть регулярное выражение, определяющее язык двоичных чисел с плавающей точкой, заданный грамматикой G.

М.Ф.Степанов

Системное программное обеспечение

Построение конечного автомата на основе леволинейной грамматики

На основе имеющейся регулярной грамматики можно построить эквивалентный ей КА и, наоборот, для заданного КА можно построить эквивалентную ему регулярную грамматику.

Это очень важное утверждение, поскольку регулярные грамматики используются для определения лексических конструкций языков программирования. Создав автомат на основе известной грамматики, мы получаем распознаватель для лексических конструкций данного языка. Таким образом, удается решить задачу разбора для лексических конструкций языка, заданных произвольной регулярной грамматикой. Обратное утверждение также полезно, поскольку позволяет узнать грамматику, цепочки языка которой допускает заданный автомат.

Все языки программирования определяют нотацию записи «слева направо». В той же нотации работают и компиляторы. Поэтому далее рассмотрены алгоритмы для леволинейных грамматик. Доказано, что аналогичные построения можно выполнить и для праволинейных грамматик.

Задача формулируется следующим образом:

¾имеется леволинейная грамматика G(VT,VN,P,S), задающая язык L(G),

¾необходимо построить эквивалентный ей конечный автомат M(Q,V,δ,q0,F), задающий тот же язык: L(G) = L(M).

Задача решается в два этапа:

1.Исходную леволинейную грамматику G необходимо привести к автоматному виду G'.

2.На основе полученной автоматной леволинейной грамматики G'(VT,VN',P',S) строится искомый

автомат M(Q,V,δ,q0,F).

Алгоритм преобразования к автоматному виду был рассмотрен выше, поэтому здесь рассмотрим только алгоритм построения КА на основе автоматной леволинейной грамматики.

Построение КА M(Q,V,δ,q0,F) на основе автоматной леволинейной грамматики G(VT,VN,P,S) выполняется по следующему алгоритму:

Шаг 1. Строим множество состояний автомата Q. Состояния автомата строятся таким образом, чтобы каждому нетерминальному символу из множества VN грамматики G соответствовало одно состояние из множества Q автомата М. Кроме того, во множество состояний автомата добавляется еще одно дополнительное состояние, которое будем обозначать Н. Сохраняя обозначения нетерминальных символов грамматики G, для множества состояний автомата М можно записать: Q=VN {H}.

Шаг 2. Входным алфавитом автомата М является множество терминальных символов грамматики G: V = VT.

Шаг 3. Просматриваем всё множество правил исходной грамматики.

Если встречается правило вида А→t P, где A VN, t VT, то в функцию переходов δ(H,t) автомата М добавляем состояние A: Aδ(H,t).

Если встречается правило вида А→Bt P, где A,B VN, t VT, то в функцию переходов δ(B,t) автомата М добавляем состояние A: Aδ(B,t).

Шаг 4. Начальным состоянием автомата М является состояние Н: q0 = Н.

Шаг 5. Множество конечных состояний автомата М состоит из одного состояния. Этим состоянием является состояние, соответствующее целевому символу грамматики G: F = {S}.

На этом построение автомата заканчивается.

Рассмотрим грамматику G({"a","(","*",")","{","}"},{S,C,К),P,S) (символы а, (, *, ), {, } из множества терминальных символов грамматики взяты в кавычки, чтобы выделить их среди фигурных скобок, обозначающих само множество):

Р: S → С*) | К}

С → (* | Са | С{ | С} | С( | С* | С) К → { | Ка | К( | К* | К) | К{

Это леволинейная регулярная грамматика. Преобразование ее к автоматному виду уже было выполнено ранее (в разделе «Регулярные и автоматные грамматики»).

Получим леволинейную автоматную грамматику следующего вида: G'( {"a","(","*",")","{","}"} , {S,S1,C,C1,K},P',S):

24	М.Ф.Степанов

Разработка компонентов транслятора

Р':	S → S1) \| К}
	S1 → С*
	С → С1* \| Са \| C{ \| C} \| C( \| C* \| C)
	C1 → (
	K → { \| Ka \| K( \| K* \| K) \| K{
	Для удобства переобозначим нетерминальные символы С1 и S1 символами D и Е.
	Получим грамматику
	G'( {"a","(","*",")","{","}"} , {S,E,C,D,K},P',S):
Р':	S → E) \| К}
	E → С*
	С → D* \| Са \| C{ \| C} \| C( \| C* \| C)
	D → (
	K → { \| Ka \| K( \| K* \| K) \| K{

Построим конечный автомат M(Q,V,δ,q0,F), эквивалентный указанной грамматике. Шаг 1. Строим множество состояний автомата.

Получаем: Q = VN {H} = {S,E,C,D,K,H}.

Шаг 2. В качестве алфавита входных символов автомата берем множество терминальных символов грамматики. Получаем: V = {"а","(","*",")","{","}"}.

Шаг 3. Рассматриваем множество правил грамматики.

Для правил S→Е) | К} имеем δ(Е,")") = {S}; δ(K,"}") = {S}.

Для правила Е→С* имеем δ(С,"*") = {Е}.

Для правил С→D* | Са | С{ | С} | С( | С* | С) имеем δ(0,"*") = {С}; δ(С,"а") = {С}; δ(С,"{") = {С}; δ(С,"}") = {С}; δ(С,"(") = {С}; δ(С,"*") = {Е,С}; δ(С,")") = {С}.

Для правила D→( имеем δ(Н,"(") = {D}.

Для правил К → { | Ка | К( | К* | К) | К{ имеем δ(Н,"{") = {К}; δ(К,"а") = {К}; δ(К,"(") = {К}; δ(К,"*") = {К}; δ(К,")") = {К}; δ(К,"{") = (К}.

Шаг 4. Начальным состоянием автомата является состояние q0 = H.

Шаг 5. Множеством конечных состояний автомата является множество F={S}. Выполнение алгоритма закончено.

В итоге получаем автомат M({S,E,С,D,К,Н}, ("а","(", "*",")","{","}"},δ,H,{S}) с функцией переходов:

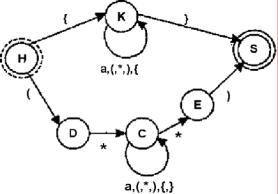
δ(Н,"{") = {К}; δ(Н,"(") = {D}; δ(К,"а") = {К}; δ(К,"(") = {К}; δ(К,"*") = {К}; δ(К,")") = {К}; δ(К,"{") = (К); δ(К,"}") = {S}; δ(D,"*") = {С}; δ(С,"а") = {С}; δ(С,"{") = {С}; δ(С,"}") = {С}; δ(С,"(") = {С}; δ(С,"*") = {Е,С}; δ(С,")") = {С}; δ(Е,")") = {S}

Граф переходов этого автомата изображен на рис. 8.

Рис. 8. Недетерминированный КА для языка комментариев в Borland Pascal

Это недетерминированный конечный автомат, поскольку существует состояние, в котором множество, получаемое с помощью функции переходов по одному и тому же символу, имеет более одного следующего состояния. Это состояние С и функция δ(С,"*")={Е,С}.

Моделировать поведение недетерминированного КА— непростая задача, поэтому можно

М.Ф.Степанов

Системное программное обеспечение

построить эквивалентный ему детерминированный КА. Полученный таким путем КА можно затем минимизировать.

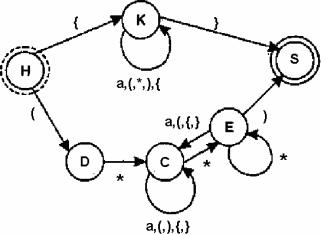
В результате всех преобразований получаем детерминированный конечный автомат М'({S,Е,С,D,К,Н},{"а","(","*",")","{","}"},δ,H,{S}) с функцией переходов (см. рис. 9):

δ'(Н,"{") = {К}; δ'(Н,"(") = {D}; δ'(К,"а") = {К}; δ'(К,"(") = {К}; δ'(К,"*")= {К}; δ'(К,")")={К}; δ'(К,"{") = (К); δ'(К,"}") = {S}; δ'(D,"*")={С}; δ'(С,"а") = {С}; δ'(С,"{")={С}; δ'(С,"}") = {С}; δ'(С,"(")={С}; δ'(С,")") = {С}; δ(С,"*") = {Е}; δ(E,"a")={С}; δ(E,"{")={С}; δ(E,"}") = {С}; δ(E,"(") = {С}; δ(E,"*") = {E}; δ(Е,")") = {S}

Рис. 9. Детерминированный КА для языка комментариев в Borland Pascal

На основании этого автомата можно легко построить распознаватель. В данном случае мы можем получить распознаватель для двух типов комментариев языка программирования Borland Pascal, если учесть, что а может означать любой алфавитно-цифровой символ, кроме символов (, *, ),

{, }.

Пример построения лексического анализатора

Теперь можно рассмотреть практическую реализацию лексических анализаторов. В принципе, компилятор может иметь в своем составе не один, а несколько лексических анализаторов, каждый из которых предназначен для выборки и проверки определенного типа лексем.

Таким образом, обобщенный алгоритм работы простейшего лексического анализатора в компиляторе можно описать следующим образом:

¾из входного потока выбирается очередной символ, в зависимости от которого запускается тот или иной сканер (символ может быть также проигнорирован либо признан ошибочным);

¾запущенный сканер просматривает входной поток символов программы на исходном языке, выделяя символы, входящие в требуемую лексему, до обнаружения очередного символа, который может ограничивать лексему, либо до обнаружения ошибочного символа;

¾при успешном распознавании информация о выделенной лексеме заносится в таблицу лексем и таблицу идентификаторов, алгоритм возвращается к первому этапу и продолжает рассматривать входной поток символов с того места, на котором остановился сканер;

¾при неуспешном распознавании выдается сообщение об ошибке, а дальнейшие действия

зависят от реализации сканера — либо его выполнение прекращается, либо делается попытка распознать следующую лексему (идет возврат к первому этапу алгоритма).

В целом, техника построения сканеров основывается на моделировании работы детерминированных и недетерминированных КА с дополнением функций распознавателя вызовами функций обработки ошибок, а также заполнения таблиц лексем и таблиц идентификаторов. Такая техника не требует сложной математической обработки и принципиально важных преобразований

26	М.Ф.Степанов

Разработка компонентов транслятора

входных грамматик. Для разработчиков сканера важно только решить, где кончаются функции сканера и начинаются функции синтаксического разбора. После этого процесс построения сканера легко поддается автоматизации.

Лексический анализатор целочисленных констант языка С

Рассмотрим пример анализа лексем, представляющих собой целочисленные константы в формате языка С. В соответствии с требованиями языка, такие константы могут быть десятеричными, восьмеричными или шестнадцатеричными. Восьмеричной константой считается число, начинающееся с 0 и содержащее цифры от 0 до 7; шестнадцатеричная константа должна начинаться с последовательности символов 0х и может содержать цифры и буквы от а до f. Остальные числа считаются десятеричными (правила их записи напоминать, наверное, не стоит). Константа может начинаться также с одного из знаков, + или -, а в конце цифры, обозначающей значение константы, в языке С может следовать буква или две буквы, явно обозначающие ее тип:

¾u, U — unsigned;

¾h, Н — short;

¾l, L — long.

При построении сканера будем учитывать, что константы входят в общий текст программы на

языке С. Во избежание путаницы и для сокращения объема информации в примере будем считать, что все допустимые буквы являются строчными (читатели легко смогут самостоятельно расширить пример для прописных букв, которые язык С в константах не отличает от строчных).

Рассмотренные выше правила могут быть записаны в форме Бэкуса—Наура в грамматике целочисленных констант для языка С.

G({S, W, U, L, V, D, G, X, Q, Z, N}, {0...9, х, a...f, u, 1, h, }, P, S)

P:S → G | Z | D | Q | U | L | V | W W → Lu | Vu | Ul | Uh

U → Gu | Zu | Hu | Qu L → Gl | Zl | Hl | Ql

V → Gh | Zh | Hh | Qh

D → 1|2|3|4|5|6|7|8|9| N1 | N2 | N3 | N4 | N5 | N6 | N7 | N8 | N9 | D0 | Dl | D2 | D3 | D4 | D5 | D6 | D7 | D8 | D9 | Z8 | Z9 | Q8 | Q9

G → X0 | X1 | X2 | X3 | X4 | X5 | X6 | X7 | X8 | X9 | Xa | Xb | Xc | Xd | Xe | Xf | G0 | G1 | G2 | G3 | G4 | G5 | G6 | 67 | 68 | G9 | Ga | Gb | Gc | Gd | Ge | Gf

X → Zx

Q → Z0 | Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | Z7 | Q0 | Q1 | Q2 | Q3 | Q4 | Q5 | Q6 | Q7 Z → 0 | N0

N → + | -

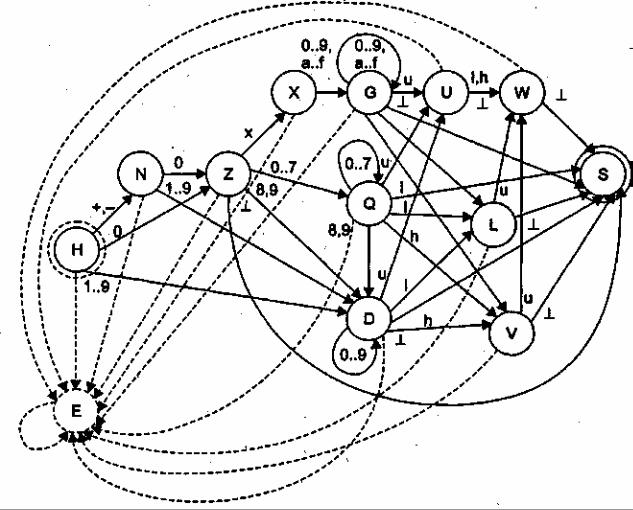
Эта грамматика является леволинейной автоматной регулярной грамматикой. По ней можно построить КА, который будет распознавать цепочки входного языка. Граф переходов этого автомата приведен на рис. 10. Видно, что построенный автомат является детерминированным КА, поэтому в дальнейших преобразованиях он не .нуждается. Начальным состоянием автомата является состояние Н.

Приведем автомат к полностью определенному виду — дополним его новым состоянием Е, на которое замкнем все дуги неопределенных переходов. На графе автомата дуги, идущие в это состояние, не нагружены символами — они обозначают функцию перехода по любому символу, кроме тех символов, которыми уже помечены другие дуги, выходящие из той же вершины графа (такое соглашение принято, чтобы не загромождать обозначениями граф автомата). На рис. 10 это состояние и связанные с ним дуги переходов изображены пунктирными линиями.

При построении КА знаком были обозначены любые символы, которыми может завершаться целочисленная константа языка С. Однако в реальной программе этот символ не встречается, поскольку границы лексем в ней явно не указаны. При моделировании КА надо решить проблему определения границ лексем. Следует принять во внимание, какими реальными символами входного языка может завершаться целочисленная константа языка С.

В языке С в качестве границы константы могут выступать:

М.Ф.Степанов

Системное программное обеспечение

¾знаки пробелов, табуляции, перевода строки;

¾разделители (, ), [, ], {, }, ., :, :;

¾знаки операций +, -, *, /, &, |, ?, ~, <, >, ^, =, %.

Теперь можно написать программу, моделирующую работу указанного автомата.

Рис. 10. Граф конечного автомата для распознавания целочисленных констант языка С

2.4. Синтаксические анализаторы

Синтаксический анализатор (синтаксический разбор) — это часть компилятора, которая отвечает за выявление и проверку синтаксических конструкций входного языка. В задачу синтаксического анализа входит:

¾поиск и выделение синтаксических конструкций в тексте исходной программы;

¾установка типа и проверка правильности каждой синтаксической конструкции;

¾представление синтаксических конструкций в виде, удобном для дальнейшей генерации текста результирующей программы.

Синтаксический анализатор — это основная часть компилятора на этапе анализа. Без

выполнения синтаксического разбора работа компилятора бессмысленна, в то время как лексический разбор, в принципе, является необязательной фазой. Все задачи по проверке синтаксиса входного языка могут быть решены на этапе синтаксического разбора.

Выходом лексического анализатора является таблица лексем. Эта таблица образует вход синтаксического анализатора, который исследует только один компонент каждой лексемы — ее тип. Остальная информация о лексемах используется на более поздних фазах компиляции при

28	М.Ф.Степанов

Разработка компонентов транслятора

семантическом анализе, подготовке к генерации и генерации кода результирующей программы.

В основе синтаксического анализатора лежит распознаватель текста исходной программы, построенный на основе грамматики входного языка. Как правило, синтаксические конструкции языков программирования могут быть описаны с помощью КС-грамматик, реже встречаются языки, которые могут быть описаны с помощью регулярных грамматик.

Распознавателями для КС-языков являются автоматы с магазинной памятью — МП-автоматы

— односторонние недетерминированные распознаватели с линейно ограниченной магазинной памятью. Поэтому важно рассмотреть, как функционирует МП-автомат и как для КС-языков решается задача разбора — построение распознавателя языка на основе заданной грамматики.

Более подробную информацию можно получить в [2, 3, 10, 11, 23, 28, 36].

МЕТОДИКА РАБОТЫ

Контрольная работа выполняется в следующем порядке:

1.Определение подлежащей решению задачи обработки информации (функциональная задача) в соответствии с приложением 1.

2.Разработка языка постановки задач пользователем (входной язык) системы решения функциональной задачи.

3.Разработка языка внутреннего представления задачи в системе решения функциональной

задачи.

4.Разработка и исследование регулярной грамматики, описывающей входной язык для использования на этапе лексического анализа транслятора постановки задачи на входном языке во внутреннее представление [2, 3, 22, 23].

5.Разработка и исследование конечного автомата, представляющего собой математическую модель лексического анализатора транслятора постановки задачи на входном языке во внутреннее представление [2, 3, 22, 23].

6.Разработка и исследование контекстно-свободной грамматики, описывающей входной язык для использования на этапе синтаксического анализа [2, 3, 22, 23].

7.Разработка управляющих таблиц синтаксического анализатора в соответствии с заданным вариантом [2, 3, 22, 23].

Проиллюстрируем этапы выполнения контрольной работы на примере.

Рассмотрим процесс разработки системы обработки информации, осуществляющей решение

дифференциального уравнения вида x& = Ax , x Rn , A Rn ×Rn при начальных условиях x( t0 ) = x0

на временном отрезке t [ t0 ,tk ] .

Исходными данными в данной задаче являются параметры дифференциального уравнения (матрица A ), начальные условия x0 , интервал анализа [ t0 ,tk ] , шаг интегрирования h .

Искомым результатом в данной задаче являются массивы чисел ax и at , представляющие собой значения вектора x в моменты времени t , необходимые для построения графиков переходных процессов.

Для удобства взаимосвязи с компонентами системы решения функциональной задачи разработаем структуру данных, включающую как постановку задачи, так и результаты ее решения. Пример подобной структуры на языке С приведен на листинге 1. Указанная структура данных, по существу, представляет собой язык внутреннего представления задачи.

Листинг 1. Объявление структуры task struct task

{

int n; double *dA; double *dx0;

double t0, tk; double h;

М.Ф.Степанов

Системное программное обеспечение

int N; double *at; double *ax;

}

Входной язык должен быть проблемно-ориентированным и предоставлять удобные средства для описания исходных данных задачи. Например, наподобие входного языка системы МАТЛАБ:

n=3;

A=[0 1 0; 0 0 1; -1,5 -2,6 -3.7]; x0=[-1,9;0;0];

t0=-1,1; tk=+10,5; h=0,01;

Семантика обозначений переменных здесь задана в соответствии с задачей.

Анализ входного языка включает несколько этапов: лексический анализ, синтаксический

анализ, семантический анализ, подготовка к генерации, генерация выходного текста.

На каждом из перечисленных этапов используется различная информация о входном языке, а поэтому его описание на различных этапах анализа может быть различным: наиболее упрощенное на этапе лексического анализа и более полное на следующих этапах.

Для этапа лексического анализа разработаем правоассоциативную регулярную грамматику, правила которой имеют вид

S::=t|tN, t VT, S,N VN.

Язык содержит 5 типов предложений, которые могут следовать в заданном порядке. Элементы массивов являются действительными числами со знаком. В учебных целях, для простоты, полагаем, что действительные числа представляются в формате с фиксированной точкой (запятой). При этом дробная часть может быть опущена вместе с разделительной точной (запятой). Знак "+" (плюс) может быть опущен. В этом случае считается, что число положительное. Элементы массивов перечисляются через пробел по строкам, которые разделяются точкой с запятой.

Данный язык может быть задан, например, грамматикой

G1(VT,VN,P, <задача>),

где <задача> - начальный символ грамматики,

VT = {n|A|x|t|k|h|0|1|2|3|4|5|6|7|8|9|.|+|-|[|]|;|,|=| } – словарь терминальных символов, где " " –

обозначает пробел,

VN = {<задача> | <размерность> | <значение размерности> | <матрица А> | <элементы матрицы А> | <все элементы матрицы А> | <элемент матрицы А> | <дробь элемента матрицы А> | <x0> | <все элементы x0> | <элемент x0> | <дробь элемента x0> | <t0> | <значение t0> | <дробь значения t0> | <tk> | <значение tk> | <дробь значения tk> | <h> | <значение h> | <дробь значения h> | <остаток задачи1> |<остаток задачи2> | <остаток задачи3> | <остаток задачи4> | <остаток задачи5> | <остаток задачи6> | <остаток задачи7> | <остаток задачи8> | <остаток задачи9> | <остаток задачи10> | <остаток задачи11> | <остаток задачи12> | <остаток задачи13> | <остаток задачи14> | <Успех>} – словарь нетерминальных символов,

P – правила подстановки:

<задача>::=n<размерность> <размерность>::= =<значение размерности>

<остаток задачи1>::=A<матрица А> | '\r'<остаток задачи1> | '\n'<остаток задачи1> <матрица А>::= =<элементы матрицы А> <элементы матрицы А>::=[<строка элементов матрицы А>

<строка элементов матрицы А>::= <элемент матрицы А> | -<элемент матрицы А> |

30	М.Ф.Степанов

<<< < Предыдущая 1 23 / 73 4 5 6 7 > Следующая >>>

Соседние файлы в папке kWork

#
11.02.2014910.81 Кб63ssw_cw.pdf
#
11.02.20141.01 Mб53SSW_kw.pdf
#
11.02.2014497.5 Кб57SSW_kw_Appendix.pdf