5. Передача сигналов и модуляция.

В современных телекоммуникационных системах сигналы передают в цифровом виде. Для этого непрерывные сигналы подвергают дискретизации во времени, а затем полученные выборки сигнала заменяют целыми числами (числа могут иметь разные знаки) (рис.5.1). Далее числа представляют в двоичном виде и передают в виде потока логических нулей и единиц.

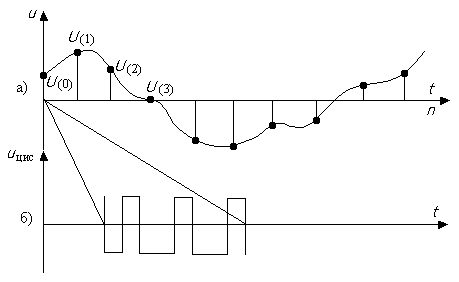
Рис 5.1. Преобразование аналогового сигнала в цифровую форму

Основой такого представления сигналов является теорема Котельникова (теорема отсчетов).

Теорема Котельникова (отсчетов): если наивысшая частота в спектре сигнала s(t) меньше, чем f_m, то функцию s(t) полностью определяет последовательность ее значений в моменты времени, отстоящие друг от друга не более чем на 1/(2 f_m) секунд.

Реальный сигнал: логические нули и единицы, можно передавать различным образом, Например, в виде последовательности биполярных прямоугольных импульсов (рис.5.2).

Рис.5.2. Последовательность сигналов, соответствующих символам 10010111

Другой вариант передачи – последовательность синусоидальных символов (рис.5.3):

. (5.1)

Рис.5.3. Сигнал с синусоидальными символами.

Для формирования и передачи сигналов необходимо знать их спектр. S(ω) – спектральную функцию, или просто, спектр одного импульса, вычисляют как

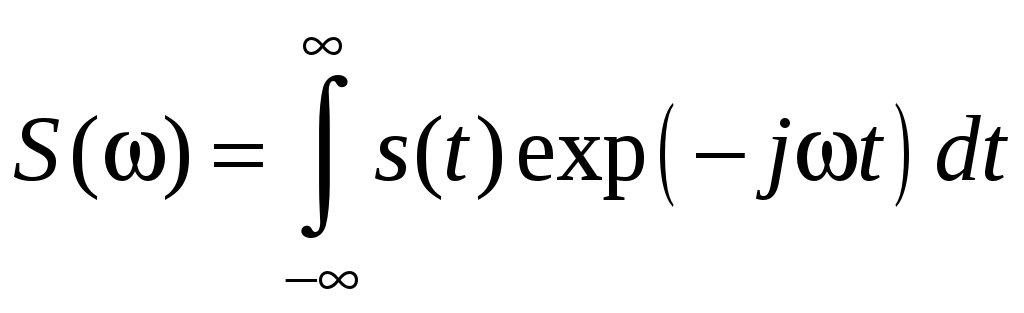. (5.2)

Так как чередование “0” и “1” случайно, то спектры отдельных временных интервалов сигнала будут также случайными. При этом спектральные характе-ристики информационных сигналов тоже случайны. Обобщенной спектральной характеристикой цифрового сигнала является энергетический спектр G(f), т.е. усредненная мощность, приходящаяся на 1 герц: G(f) (Вт/Гц).

Если на временном интервале передачи цифрового сигнала появление “0” и “1” равновероятно (вероятность того и другого равна 0,5), а сами “0” и “1” передают в виде импульсов одинаковой формы, но разной полярности, то энергетический спектр G(f) и спектр одного импульса S(f) = S() связаны между собой соотношением

, (5.3)

где f_T = 1/T₀ – частота следования бит.

Энергетические спектры сигналов с прямоугольными и синусоидальными символами представлены на рис.5.4.

Рис. 5.4. Спектральные плотности сигналов

При передаче цифровых сигналов вводят понятие необходимой полосы частот ΔF_н, которую определяют как минимальную полосу частот данного класса излучения, достаточную для передачи сигнала с требуемой скоростью и качеством. Как показано на рис.5.4, цифровые сигналы в виде последовательности прямоугольных импульсов или других форм имеют бесконечный спектр. Конечному по ширине спектру соответствует бесконечный по длительности сигнал. Следовательно, импульсы, передающие соседние биты, будут накладываться друг на друга, что называют межсимвольной интерференцией. Наличие межсимвольной интерференции увеличивает вероятность ошибок при приеме.

Минимальная полоса, требуемая для передачи информационного сигнала,

П_В  f_T/2 = В/2,

где В – скорость передачи потока данных.

Для передачи по радиоканалу производят модуляцию информационным сигналом колебаний радиочастоты (несущей). Процесс модуляции состоит в изменении каких-либо параметров радиочастоты (амплитуды, частоты, фазы) по закону модулирующего информационного сигнала. Наиболее эффективно используют частотный ресурс при фазовой модуляции (манипуляции).

Простейшим случаем цифровой модуляции является двоичная фазовая модуляция (манипуляция) 2-ФМ (BPSK, Binary Phase Shift Keying), при которой для передачи любого из двух двоичных символов 0 или 1 используют два значения начальной фазы отрезка гармонического колебания на интервале [0; T]:

;

.

Сигналы 2-ФМ, являясь противоположными сигналами, обладают наилучшей (потенциальной) помехоустойчивостью, т.е. при заданном отношении сигнал/шум имеют наименьшую вероятность ошибочного приема, однако ее достижение возможно лишь в таких приемных устройствах, в которых обеспечивается постоянство фазы опорного колебания, например, при передаче пилотного (опорного) сигнала в стандартах сотовой связи с кодовым разделением каналов.

Формирование сигнала 2-ФМ осуществляют путем умножения модулирующего сигнала a(t) на колебания несущей частоты U₀ cos ₀t. Эту операцию выполняют в балансных модуляторах (смесителях) с последующей фильтрацией частот высших порядков. Полоса радиосигнала П_рад в 2 раза шире полосы модулирующего сигнала П_мод, т.е. минимум П_рад = В.

В тех случаях, когда сигнал опорной фазы отсутствует, используют относительную дифференциальную (дифференциальную) двоичную фазовую модуляцию (2-ОФМ) (DBPSK, Differential Binary Phase Shift Keying), при которой информация содержится не в абсолютном значении начальных фаз, а в разности начальных фаз двух соседних сигналов.

Например, при передаче символа 0 начальная фаза на текущем тактовом интервале остается неизменной по отношению к предыдущему интервалу, а при передаче символа 1 происходит изменение фазы колебания на π. По такому же правилу работает и приемник при принятии решения о переданном символе. В табл.5.1 показано, как меняется фаза радиочастотного сигнала при модуляции 2-ОФМ.

Таблица 5.1

Информационные биты	0	1	0	0	1	1	1	1	0	0	1	0
Текущая фаза, 	0	π	π	π	0	π	0	π	π	π	0	0

Сигналы с 2-ФМ обладают максимальной помехозащищенностью, но скорость передачи в радиоканале при этом минимальна. Для повышения эффективности передачи используют многопозиционные сигналы, когда сигнал на сигнальной плоскости имеет более двух позиций.

На рис.5.5 показаны сигнальные диаграммы (созвездия) для сигналов с многопозиционной фазовой манипуляцией для M=2, 4, 8.

Широко используемым вариантом многопозиционной фазовой модуляции является четырехпозиционная, или четырехпозиционная (квадратурная) фазовая модуляция (манипуляция) 4-ФМ (QPSK, Quadrature Phase Shift Keying), которая, с одной стороны, позволяет в два раза повысить скорость передачи информации, а с другой – обладает помехоустойчивостью, ненамного худшей, чем 2-ФМ.

Диаграмма сигнала 4-ФМ (произвольная) приведена на рис.5.5б.

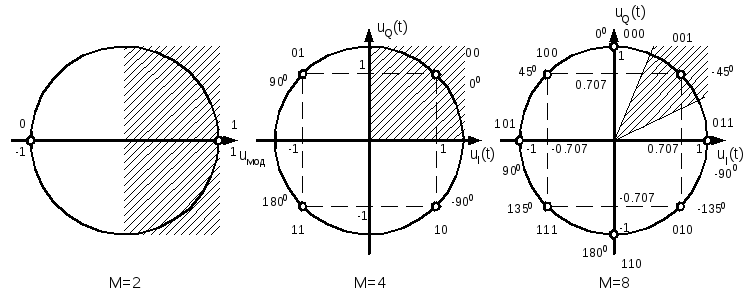
а) б) в) Рис.5.5. Сигнальные созвездия для М-ФМ

Любое из 4-х состояний сигнала можно представить как сумму двух составляющих:

, (5.4)

где U_I (inphase) – амплитуда синфазной составляющей,

U_Q (quadrature) – амплитуда квадратурной составляющей

Схема квадратурного модулятора приведена на рис.5.6.

Рис.5.6. Схема квадратурного модулятора

На рис. 5.6 u_ЦИС – информационный цифровой сигнал;

ПК – преобразователь кода;

Модулятор a_I –модулятор синфазной составляющей;

Модулятор a_Q –модулятор квадратурной составляющей;

 - сумматор.

При манипуляции 4-ФМ каждое значение фазы содержит информацию о двух битах, а символьная скорость f_s передачи в синфазном и квадратурном каналах в 2 раза ниже скорости передачи данных.

(5.5)

Для приема сигнала 4-ФМ используют квадратурный синхронный детектор, схема которого приведена на рис.5.7, где

БМ I - балансный модулятор выделения синфазной составляющей;

БМ Q - балансный модулятор выделения квадратурной составляющей;

Рис.5.7. Схема квадратурного синхронного детектора

Сигналы на выходе БМI и БМQ

После фильтрации радиочастотных составляющих в ФНЧ получаем исходные модулирующие сигналы U_I(t) и U_Q.(t).

Модуляцию 4-ФМ можно использовать, когда есть опорный (пилотный) сигнал. Тогда можно определять фазу, соответствующую передаче двух бит в соответствии с рис.5.5. Если пилотный сигнал отсутствует, то по аналогии с 2-ОФМ применяют 4-ОФМ (четырехпозиционную относительную фазовую модуляцию; DQPSK – Differential QPSK).

Цена, которую приходится платить за увеличение эффективности использования канального ресурса – снижение помехозащищенности передачи, т.е. увеличение коэффициента ошибок в сравнении с 2-ФМ. При сопоставлении с рис. 5.5. а, где принятый бит определяют на полуплоскости, в случае 4-ФМ принятый символ (2 бита) определяют в квадранте (рис. 5.5б). Следовательно, вероятность появления ошибки при переходе от 2-ФМ к 4-ФМ возрастает в 2 раза.

На рис.5.5в в приведен сигнал 8-ФМ (восьмипозиционной фазовой модуляции). В этом сигнале один сигнальный символ содержит информацию о трех битах. Каждое соседнее состояние отличается на 1 бит (код Грея). Длительность модулирующих символов , частота модулирующих символов , полоса сигнала 8-ФМ .

Помехозащищенность 8-ФМ ниже, чем 4-ФМ. Если при 4-ФМ принятый символ определяют в квадранте (рис.5.5б), то при 8-ФМ в секторе (рис.5.5 в). Для получения того же значения BER порядка 5*10^-4 и лучше при 8-ФМ необходимо увеличение отношения сигнал/помеха в сравнении с 4-ФМ на 4 дБ. По аналогии с 8-ФМ следующим был бы сигнал 16-ФМ, однако большей помехозащищенностью обладают сигналы квадратурной амплитудной модуляции КАМ.

Модуляцию 4-ФМ (4-ОФМ) широко применяют в стандартах сотовой связи с кодовым разделением каналов, в стандартах беспроводного доступа (Wi-Fi, WiMAX), а модуляцию 8-ОФМ в стандарте GSM (технология EDGE).

В общем случае полосу модулированного радиосигнала при числе позиций радиосигнала M.определяют по формуле

(5.6)

В сигналах квадратурной амплитудной модуляции КАМ (QAM – Quadrature Amplitude Modulation) изменяются как фаза, так и амплитуда сигнала. Созвездие позиций сигнала 16-КАМ приведено на рис.5.8. Сигнал 16-КАМ имеет 3 амплитуды и 12 фаз.

Рис.5.8. Созвездие сигнала 16-КАМ

Модуляция с непрерывной фазой. Одной из проблем при построении передатчиков устройств мобильной связи является повышение их КПД. Особенно это важно для передатчиков мобильных станций, для чего транзисторы выходных усилителей мощности должны работать в энергетически выгодных режимах, что возможно при постоянстве огибающей выходного сигнала.

С этой целью переходят от модуляции напряжением прямоугольной формы (2-ФМ, 4-ФМ, 8-ФМ) к модулирующим сигналам, где отсутствуют разрывы первого рода. Наиболее часто используют последовательности синусоидальных импульсов (рис.5.3), что равнозначно переходу от фазовой манипуляции к частотной, причем девиация частоты f жестко связана со скоростью передачи бит В в радиоканале соотношением

(5.7)

Такую модуляцию называют ЧММС (MSK – Minimum Shift Keying) – частотной модуляцией с минимальным сдвигом. Так в GSM передаче “0” соответствует частота , а передаче “1” . Во время передачи одного бита (Т Є 0 … Т_В) , так что при t =T_B = 1/B . Величина 2f составляет минимальный сдвиг частот, при котором можно реализовать модуляцию с непрерывной фазой. Временные диаграммы параметров ЧММС сигнала приведены на рис.5.9.

Рис. 5.9. Временные диаграммы при ЧММС