
- •Міністерство освіти і науки україни
- •Передмова
- •Склад модулів “інженерна графіка”, розподіл часу на їх засвоєння, терміни контролю
- •Умовні позначки
- •1. Загальні правила виконання розрахунково-графічних робіт
- •Вибір варіанта на контрольну роботу (заочна форма навчання)
- •Шкала меж позитивних оцінок за модулем
- •Критерії оцінювання знань
- •Рейтингові бали за шкалою оцінок
- •Методичні поради до виконання
- •Багатоваріантне завдання на розрахунково-графічні роботи № 1, 2
- •Завдання 2 Відстань від точки до площини. Паралельність площин
- •Методичні поради до виконання
- •Завдання 3 Перетин площин
- •Методичні поради до виконання
- •Багатоваріантне завдання на розрахунково-графічну роботу № 3
- •Багатоваріантне завдання на розрахунково-графічну роботу № 4
- •Завдання 5 Перетин поверхні площиною
- •Методичні поради до виконання
- •Багатоваріантне завдання на розрахунково-графічну роботу №5
- •Завдання 6 Комплексний кресленик моделі
- •Методичні вказівки
- •Багатоваріантне завдання на розрахунково-графічну роботу № 6
- •Завдання 7 Кресленик електричної схеми приладу
- •Методичні вказівки
- •3. Запитання зі контролю знань
- •4. Тест-контроль
- •Відповіді на тестові запитання
- •Основна
- •Додаткова
Завдання 2 Відстань від точки до площини. Паралельність площин
(приклад завдання рис. 3)
Дано: координати точок А,В,С і D (табл. 7).
Визначити:
-
відстань d0 від точки D до площини
 [АВС];
[АВС]; -
площину
 ,
паралельну площині
,
паралельну площині
 [АВС]
і віддалену від неї на відстань
[АВС]
і віддалену від неї на відстань
 ;
; -
видимість перпендикуляра d і площини
 відносно площини
відносно площини
 ,
обмеженою трикутником [ABC].
,
обмеженою трикутником [ABC].
Методичні поради до виконання
-
Площину
 [АВС]
і точку D
побудувати за координатами точок,
наведеними в таблиці 7.
[АВС]
і точку D
побудувати за координатами точок,
наведеними в таблиці 7. -
Щоб визначити відстань від точки до площини, необхідно з точки D опустити перпендикуляр L, на площину
 [ABC],
використовуючи умову перпендикулярності
цих геометричних образів, далі визначаємо
точку їх зустрічі К
і для цього, уводимо допоміжну січну
площину
[ABC],
використовуючи умову перпендикулярності
цих геометричних образів, далі визначаємо
точку їх зустрічі К
і для цього, уводимо допоміжну січну
площину
 ,
яка повинна бути проекціювальною.
,
яка повинна бути проекціювальною. -
Справжню відстань від точки до площини d0 = [D0K0] визначити методом прямокутного трикутника.
-
Паралельну площину
 задати двома перетинаючимися прямими
b і a,
які проходять через точку L,
що розташована посередині відрізка
прямої [DK],
для цього використовуємо умову
паралельності двох площин. Середину
відрізка прямої [DK],
визначаємо спочатку на справжній
величині (діленням її навпіл) та методом
протилежного проекціювання переносимо
на горизонтальну і фронтальну проекції
перпендикуляра.
задати двома перетинаючимися прямими
b і a,
які проходять через точку L,
що розташована посередині відрізка
прямої [DK],
для цього використовуємо умову
паралельності двох площин. Середину
відрізка прямої [DK],
визначаємо спочатку на справжній
величині (діленням її навпіл) та методом
протилежного проекціювання переносимо
на горизонтальну і фронтальну проекції
перпендикуляра. -
Видимість геометричних образів на кресленику визначається способом конкуруючих точок (у прикладі завдання – точки N і 3). При оформленні кресленика необхідно вважати, що площина
 обмежена трикутником [ABC],
площина
обмежена трикутником [ABC],
площина
 – двома проміннями a
і b, що
виходять з точки L.
– двома проміннями a
і b, що
виходять з точки L.
Завдання 3 Перетин площин
(приклад завдання рис. 4)
Дано: координати точок А, B і С (табл. 8).
Визначити:
-
площину
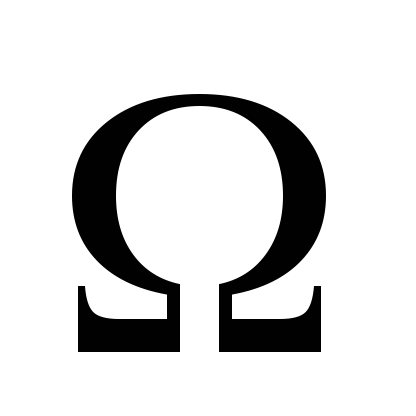 ,
перпендикулярну до сторони [AC]
площини
,
перпендикулярну до сторони [AC]
площини
 [ABC] та
яка проходить через точку В;
[ABC] та
яка проходить через точку В; -
лінію перетину площин
 і
і
 ;
; -
взаємну видимість ділянок площин
 і
і
 .
.
Методичні поради до виконання
-
Площини
 [АВС]
і
[АВС]
і
 [DEF]
побудувати за координатами точок згідно
варіанта завдання (табл. 8).
[DEF]
побудувати за координатами точок згідно
варіанта завдання (табл. 8).
-
Лінію перетину визначити за допомогою площин посередників. У прикладі за такі площини прийнято фронтально-проекціювальні площини Q2 i P2, які проходять через фронтальні проекції сторін |АС| і |ВС| площини [АВС], а в перетині з площиною [DFC] утворюють сліди. Таким чином, задача зводить на визначення горизонтальних проекцій слідів допоміжних проекціювальних площин, які в перетині з горизонтальною проекцією сторони через яку вони проходять, визначають шукані точки лінії перетину площин К і М.
 Рис.
3. Приклад завдання №2 – "Комплексний
кресленик площини"
Рис.
3. Приклад завдання №2 – "Комплексний
кресленик площини"
-
Взаємну видимість ділянок площин визначити способом конкуруючих точок (у прикладі завдання фронтально – конкуруючі точки 6–7 і 4–8).
Таблиця 8
Багатоваріантне завдання на розрахунково-графічну роботу № 3
|
Варіант |
Координати точки (x, y, z), мм |
|||||
|
А |
В |
С |
D |
E |
F |
|
|
1 |
20; 10; 20 |
85; 80; 90 |
135; 50; 30 |
70; 85; 0 |
0; 35; 90 |
120; 20; 60 |
|
2 |
115; 20; 10 |
50; 90; 80 |
0; 30; 50 |
65; 0; 85 |
135; 90; 35 |
15; 60; 20 |
|
3 |
115; 10; 20 |
50; 80; 90 |
0; 50; 30 |
65; 85; 0 |
135; 35; 90 |
15; 20; 60 |
|
4 |
20; 20; 10 |
85; 90; 80 |
135; 30; 50 |
70; 0; 85 |
0; 90; 35 |
120; 60; 20 |
|
5 |
120; 20; 30 |
50; 90; 100 |
0; 35; 70 |
70; 5; 105 |
135; 80; 50 |
15; 80; 20 |
|
6 |
15; 30; 20 |
85; 100; 90 |
135; 70; 35 |
65; 105; 5 |
0; 50; 80 |
120; 20; 80 |
|
7 |
120; 30; 20 |
50; 100; 90 |
0; 70; 35 |
70; 105; 5 |
135; 50; 80 |
15; 20; 80 |
|
8 |
15; 20; 30 |
85; 90; 100 |
135; 35; 70 |
65; 5; 105 |
0; 80; 50 |
120; 80; 20 |
|
9 |
120; 20; 80 |
50; 90; 10 |
0; 20; 45 |
115; 0; 5 |
70; 90; 105 |
15; 65; 90 |
|
10 |
0; 80; 20 |
70; 10; 90 |
120; 45; 20 |
5; 5; 0 |
50; 105; 90 |
105; 90; 65 |
|
11 |
0; 20; 80 |
70; 90; 10 |
120; 20; 45 |
5; 0; 5 |
50; 90; 105 |
105; 65; 90 |
|
112 |
120; 80; 20 |
50; 10; 90 |
0; 45; 20 |
115; 5; 0 |
70; 105; 90 |
15; 90; 65 |
|
13 |
115; 80; 30 |
50; 10; 100 |
0; 65; 65 |
65; 90; 100 |
130; 0; 0 |
15; 35; 20 |
|
14 |
15; 30; 80 |
80; 100; 10 |
130; 65; 65 |
65; 100; 90 |
0; 0; 0 |
115; 20; 35 |
|
15 |
15; 80; 30 |
80; 10; 100 |
130; 65; 65 |
65; 90; 100 |
0; 0; 0 |
115; 35; 20 |
|
16 |
115; 30; 80 |
50; 100; 10 |
0; 65; 65 |
65; 100; 90 |
130; 0; 0 |
15; 20; 35 |
|
17 |
150; 25; 50 |
70; 95; 90 |
0; 0; 0 |
10; 40; 85 |
150; 90; 35 |
110; 10; 10 |
|
18 |
0; 50; 25 |
80; 90; 95 |
150; 0; 0 |
140; 85; 40 |
0; 35; 90 |
40; 10; 10 |
|
19 |
0; 25; 50 |
80; 95; 90 |
150; 0; 0 |
140; 40; 85 |
0; 90; 35 |
40; 10; 10 |
|
20 |
150; 50; 25 |
70; 90; 95 |
0; 0; 0 |
10; 85; 40 |
150; 35; 90 |
110; 10; 10 |
|
21 |
115; 0; 90 |
50; 70; 25 |
0; 40; 85 |
70; 70; 110 |
135; 25; 35 |
20; 0; 0 |
|
22 |
20; 90; 0 |
85; 25; 70 |
135; 85; 40 |
65; 110; 70 |
0; 35; 25 |
115; 0; 0 |
|
23 |
115; 90; 0 |
50; 25; 70 |
0; 85; 40 |
70; 110; 70 |
135; 35; 25 |
20; 0; 0 |
|
24 |
20; 0; 90 |
85; 70; 25 |
135; 40; 85 |
65; 70; 110 |
0; 25; 35 |
115; 0; 0 |
|
25 |
120; 10; 20 |
45; 85; 90 |
0; 40; 30 |
70; 85; 0 |
130; 25; 90 |
15; 0; 40 |
|
26 |
10; 20; 10 |
85; 90; 85 |
130; 30; 40 |
60; 0; 85 |
0; 90; 25 |
115; 40; 0 |
|
27 |
10; 10; 20 |
85; 85; 90 |
130; 40; 30 |
60; 85; 0 |
0; 25; 90 |
115; 0; 40 |
|
28 |
120; 20; 10 |
45; 90; 85 |
0; 30; 40 |
70; 0; 85 |
130; 90; 25 |
15; 40; 0 |
|
29 |
140; 80; 95 |
70; 80; 100 |
0; 0; 0 |
120; 0; 0 |
50; 0; 100 |
0; 90; 35 |
|
30 |
0; 100; 80 |
70; 100; 80 |
140; 0; 0 |
20; 0; 0 |
90; 100; 0 |
140; 35; 90 |

Рис. 4. Приклад завдання №3–- "Перетин площин"
Завдання 4
Способи перетворення проекцій
001. Спосіб заміни площин проекцій.
величина двогранного кута
(приклад завдання рис. 5)
Дано: координати точок A, B, C, D (табл. 9).
Визначити:
-
багатогранник
 [ABCD];
[ABCD];
-
відстань NK=d0 між двома ребрами багатогранника, що перетинаються та її проекції – методом заміни площин проекцій;
-
величину кута
 між суміжними гранями багатогранника.
між суміжними гранями багатогранника.
Методичні поради до виконання
-
Багатогранник [ABCD] побудувати за координатами точок згідно варіанту завдання. Видимість ребер визначити за допомогою конкуруючих точок.
-
Для визначення кута
 між суміжними гранями, комплексне
креслення перетворюють таким чином,
щоб грані зайняли проекціювальне
положення; спільне ребро для суміжних
граней повинно зайняти, також,
проекціювальне положення. Тому,
визначення кута
між суміжними гранями, комплексне
креслення перетворюють таким чином,
щоб грані зайняли проекціювальне
положення; спільне ребро для суміжних
граней повинно зайняти, також,
проекціювальне положення. Тому,
визначення кута
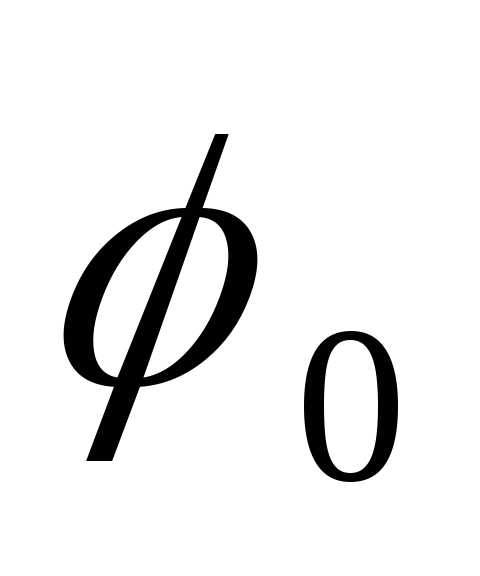 здійснюється одночасно з визначенням
відстані між ребрами, що перетинаються.
У прикладі показано визначення кута
здійснюється одночасно з визначенням
відстані між ребрами, що перетинаються.
У прикладі показано визначення кута
 між гранями [АВС]
і [АСD].
між гранями [АВС]
і [АСD].
002. Спосіб плоско паралельного переміщення.
Відстань від точки до площини.
Кут нахилу площини до площин проекцій
(приклад завдання рис. 6)
Дано: координати точок А, B, C, D (табл. 9).
Визначити:
-
площину [ABC] і точку D;
-
способом плоскопаралельного переміщення визначити відстань від точки D до площини. заданої трикутником [ABC];
-
кут нахилу площини [ABC] до горизонтальної (варіанти 1–15) чи фронтальної (варіанти 16–30) площини проекцій.
Методичні поради до виконання
-
Площину [ABC] і точку D побудувати за координатами точок згідно з варіантом завдання;
-
Для визначення дійсної величини грані за вісь обертання прийняти горизонталь чи фронталь вибраної грані. Доцільно вісь обертання побудувати зовні проекції багатогранника – це дозволить винести шукану справжню величину на вільне місце кресленика та уникнути накладення вихідних даних і ліній побудов. Якщо одне з ребер багатогранника є головною лінією, можна використовувати його як вісь обертання (у прикладі визначена величина грані |BCD| методом обертання її навколо горизонталі h, проведеної через вершину D).
-
Для визначення відстані від вершини до грані способом плоско-паралельного переміщення перетворити вибрану грань піраміди в проекціювальну, при цьому одна з головних ліній також буде проекціювальною.
-
Оскільки при розв’язуванні першої задачі головні лінії вже були побудовані, раціонально перетворювати ту ж грань (на прикладі завдання визначено відстань [А0К0] від вершини А до грані |BCD|).
-
Під час розв`язування цієї задачі необхідно враховувати, що площина до якої визначена відстань, не обмежена трикутником і може бути продовжена до перетину з перпендикуляром, опущеним до неї з протилежної вершини піраміди.
Таблиця 9
