Счетчики. Суммирующий счетчик.
В простейшем случае двоичный счетчик может быть образован из асинхронных Т-триггеров, соединенных последовательно. При этом сигналы счета a поступают на вход Т-триггера младшего разряда счетчика. Прямой выход Q триггера каждого разряда соединен со входом Т соседнего триггера более старшего разряда. Поскольку в процессе счета переключение триггеров отдельных разрядов в этом счетчике осуществляется последовательно разряд за разрядом, такой счетчик носит название счетчика с последовательным переносом. Для ликвидации неустойчивых состояний используются двухступенчатые триггера. Схема счетчика имеет следующий вид (рис. 3.13):
Рис. 3.13. Суммирующий счетчик
Числа, формируемые счетчиком, могут быть выведены из него в параллельной форме посредством одновременного опроса состояния всех разрядов счетчика.
В асинхронном Т-триггере смена состояний происходит по заднему фронту входного сигнала, поскольку двухступенчатый триггер можно рассматривать как схему, состоящую из двух триггеров (рис. 3.14):
Рис. 4.14. Асинхронный Т-триггер
Временная диаграмма работ трех разрядного асинхронного суммирующего счетчика с последовательным переносом имеет вид (рис. 3.15).
Рис. 3.15. Временная диаграмма
Вычитающий счетчик. Реверсивный счетчик.
Вычитающий счетчик также может быть построен из последовательно соединенных Т-триггеров. На вход младшего разряда счетчика поступают сигналы счета, а входы последующих разрядов соединены с инверсными выходами предшествующих триггеров (рис.3.16).
Рис. 3.16. Вычитающий счетчик
Для построения реверсивного счетчика необходимо объединить схемы суммирующего и вычитающего счетчиков. Схема асинхронного реверсивного счетчика с последовательным переносом имеет вид (рис. 3.17):
Рис. 3.17. Асинхронный реверсивный счетчик
Здесь при наличии единичного сигнала на управляющей шине I счетчик работает как суммирующий, а при наличии единичного сигнала на управляющей шине II – как вычитающий.
Одноразрядный двоичный сумматор
Одноразрядный двоичный сумматор является комбинационной схемой с тремя входами и двумя выходами (рис.3.18).
При параллельном суммировании на входы каждого разряда сумматора поступают значения цифр а и b соответствующих разрядов слагаемых и значение переноса p с младших разрядов сумматора. На выходе одноразрядного сумматора формируются значения цифры соответствующего разряда суммы S и переноса в старший разряд сумматора P.
Значения S и P таблицы истинности одноразрядного сумматора построена на основе сложения и умножения для двоичной системы счисления.
|
|
|||||
|
Таблица истинности выходов одноразрядного сумматора |
|||||
|
№ |
Входы |
Выходы |
|||
|
a |
b |
p |
S |
P |
|
|
1 |
0 |
0 |
0 |
0 |
0 |
|
2 |
0 |
0 |
1 |
1 |
0 |
|
3 |
0 |
1 |
0 |
1 |
0 |
|
4 |
0 |
1 |
1 |
0 |
1 |
|
5 |
1 |
0 |
0 |
1 |
0 |
|
6 |
1 |
0 |
1 |
0 |
1 |
|
7 |
1 |
1 |
0 |
0 |
1 |
|
8 |
1 |
1 |
1 |
1 |
1 |
Для каждого выходного сигнала составляются все комбинации входных сигналов, при которых выходные сигналы S и P принимают единичные значения:
,
.
Эти уравнения являются совершенной дизъюнктивной нормальной формой логических функций (СДНФ). В этой форме логическая функция (ЛФ) представляется в виде дизъюнкций конституэнт единицы.
Конституэнта единицы – это конъюнкция всех значений входных переменных: в прямой форме для единичных значений переменных, или в инверсной форме для нулевых значений переменных.
СДНФ позволяет записывать любые переключательные функции от двух переменных, используя только три основных логических операции И, ИЛИ, НЕ.
Следующим этапом проектирования является минимизация логических функций (не всегда возможна).
Из таблицы истинности видно, что переменная P принимает значение только для таких комбинаций входных переменных, когда хотя бы две переменные имеют единичные значения. Это можно записать в виде:
.
Анализируя функцию
S можно заметить, что
значение S равно единице,
если в комбинациях входных сигналов
присутствует хотя бы один единичный
сигнал, и нет одновременно двух единичных
значений переменных (компонента:
=
)
или есть совпадение трех входных
единичных сигналов (компонента abp),
т.е.:
Построение функциональной схемы по ПФ:
.
Для реализации ПФ для выхода Р требуется :
- три конъюнктора (схемы И) на два входа;
- дизъюнктор (схема ИЛИ) на 3 входа.
Для реализации ПФ для выхода S требуются:
- дизъюнктор (схема ИЛИ) на 3 входа;
- инвертор (схема НЕ);
- конъюнкторы (схемы И) на 2 и 3 входа;
- дизъюнктор (схема ИЛИ) на 2 входа.
Функциональная схема одноразрядного сумматора представлена на рис.3.19.
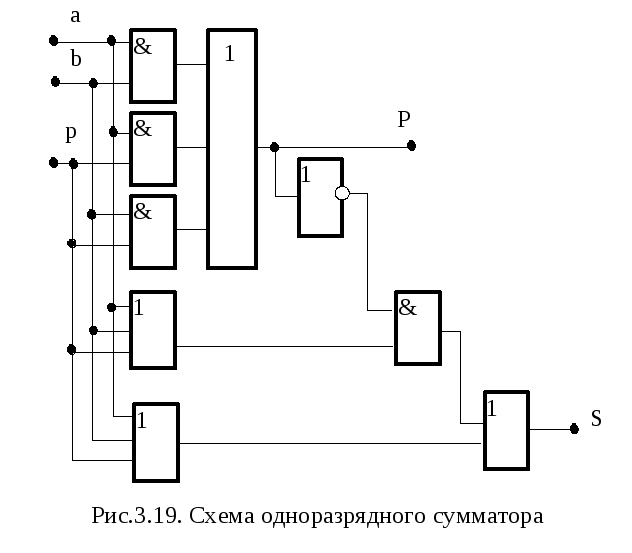
В этой схеме использована совместная минимизация уравнений, при которой для формирования разных выходных значений (S и P) используются общие логические схемы. Совместная минимизация позволяет получать схемы с минимальным количеством используемых элементарных вентилей, которое определяется по общему количеству входов. Такие схемы, как правило, имеют большую задержку выходных сигналов, которая определяется по максимальному количеству элементов пути его формирования.
По этой причине часто одноразрядный сумматор строят без совместной минимизации схем формирования выходных сигналов по уравнениям:
,
.