
- •Л.В. Батырева общая теория статистики
- •Введение
- •Тема 1. Предмет и метод статистической науки.
- •Тема 2. Статистическое наблюдение.
- •Тема 3. Статистическая сводка и группировка.
- •Тема 4. Абсолютные и относительные показатели.
- •Тема 5. Средние величины.
- •Тема 6. Показатели вариации.
- •Тема 7. Ряды динамики.
- •Средний абсолютный прирост
- •Средний темп роста
- •Средний уровень ряда:
- •Тема 8. Индексы.
- •Тема 9. Выборочное наблюдение.
- •Средняя ошибки для генеральной доли при бесповторном способе отбора;
- •Тема 10. Статистические приемы изучения взаимосвязей.
- •Зависимость среднесуточной переработки сахарной свеклы
- •Расчет межгрупповой дисперсии
- •Уравнение регрессии будет иметь вид:
- •Расчет показателей для вычисления
- •Библиографический список
- •Приложения Приложение 1
- •Продолжение Прил.1
- •Продолжение Прил. 1
- •Продолжение Прил. 1
- •Продолжение Прил. 1
- •Продолжение Прил. 1
- •Продолжение Прил. 1
- •Продолжение Прил. 1
- •Продолжение Прил. 1
- •Продолжение Прил. 1
- •Приложение 2 Значения интеграла вероятностей нормального закона распределения
- •Приложение 3 Критические значения корреляционного отношения η2 и коэффициента детерминации r2
- •Приложение 4 Критические значения f-критерия
- •Оглавление
- •Людмила Владимировна Батырева общая теория статистики Учебно-практическое пособие
- •454091, Г. Челябинск, ул. Свободы, 155/1
-
Средний абсолютный прирост
Δ![]() =
=
![]() ,
,
где n – число абсолютных приростов цепных;
Δ![]() =
=
![]() ,
,
где n – число периодов, включая базисный.
-
Средний темп роста
=![]() =
=![]() ,
,
где Пk – произведение цепных темпов роста;
n – число этих цепных темпов роста;
=![]() ,
,
где уn – конечный уровень ряда;
уо – базисный уровень ряда;
m – число периодов, включая базисный.
-
Средний уровень ряда:
а) в интервальном ряду динамики по средней арифметической простой, если интервалы равны:
![]() =
=![]() ,
,
где у – уровень ряда динамики;
n – число уровней;
б) в интервальном ряду динамики по средней арифметической взвешенной, если интервалы не равны:
![]() =
=![]() ,
,
где t – показатель времени;
в) в моментном ряду динамики по средней хронологической:
![]() =
=![]() ,
,
где у – уровень ряда
n – число уровней.
Пример 2. Имеются следующие данные об остатках сырья и материалов на складе предприятия, млн. руб.:
1/I – 500; на 1/II – 550; на 1/III – 575; на 1/IV – 560.
Определить среднемесячный остаток сырья и материалов на складе предприятия за I квартал.
Решение: По условию задачи имеем моментный ряд динамики с равными интервалами, поэтому средний уровень ряда будет исчислен по формуле средней хронологической:
![]() =
=![]() =551,7
млн. руб.
=551,7
млн. руб.
Пример 3. Имеются следующие данные о производстве продукции предприятия за 1996-2001 гг. (в сопоставимых ценах), млн. руб.:
1996г. 1997г. 1998г. 1999г. 2000г. 2001г.
101 108 110 117 122 128
Определить аналитические показатели ряда динамики производства продукции предприятия за 1996-2001 гг.:
-
абсолютные приросты (цепные и базисные);
-
темпы роста (цепные и базисные);
-
темпы прироста (цепные и базисные);
-
абсолютное значение одного процента прироста;
-
средний абсолютный прирост;
-
средний темп роста за 1996-2001 гг. и среднегодовой темп прироста;
-
среднегодовое производство продукции;
-
построить график производства продукции.
Полученные показатели представить в итоговой таблице.
Решение:
-
Определим абсолютные приросты:
цепные базисные
![]() yц
= уi –
yi-1
yц
= уi –
yi-1 ![]() yб
= уi –
yо
yб
= уi –
yо
![]() y97=108–101=7
млн. руб.
y97=108–101=7
млн. руб. ![]() y97=108–101=7
млн. руб.
y97=108–101=7
млн. руб.
![]() y98=110–108=2
млн. руб.
y98=110–108=2
млн. руб. ![]() y98=110–101=9
млн. руб.
y98=110–101=9
млн. руб.
![]() y99=117–110=7
млн. руб.
y99=117–110=7
млн. руб. ![]() y99=117–101=16
млн. руб.
y99=117–101=16
млн. руб.
![]() y2000=122–117=5
млн. руб.
y2000=122–117=5
млн. руб. ![]() y2000=122–101=21
млн. руб.
y2000=122–101=21
млн. руб.
![]() y01=128–122=6
млн. руб.
y01=128–122=6
млн. руб. ![]() y01=128–101=27
млн. руб.
y01=128–101=27
млн. руб.
-
Определим темпы роста:
цепные базисные
k =
![]() k
=
k
=
![]()
k97=![]() =1,069 k97=1,069
=1,069 k97=1,069
k98=![]() =1,018 k98=
=1,018 k98=![]() =1,089
=1,089
k99=![]() =1,064 k99=
=1,064 k99=![]() =1,158
=1,158
k00=![]() =1,043 k00=
=1,043 k00=![]() =1,208
=1,208
k01=![]() =1,049 k01=
=1,049 k01=![]() =1,267
=1,267
-
Определим темпы прироста:
цепные базисные
Δkц = kц % – 100 Δkб = k % – 100
Δk97=106,9–100=6,9 % Δk97=106,9–100=6,9 %
Δk98=101,8–100=1,8 % Δk98=108,9–100=8,9 %
Δk99=106,4–100=6,4 % Δk99=115,8–100=15,8 %
Δk00=104,3–100=4,3 % Δk00=120,8–100=20,8 %
Δk01=104,9–100=4,9 % Δk01=126,7–100=26,7 %
-
Определим абсолютное значение одного процента прироста:
А %
=
![]() или А % = 0,01 уi-1
или А % = 0,01 уi-1
А %97=1,01 млн. руб.
А %98=1,08 млн. руб.
А %99=1,1 млн. руб.
А %2000=1,17 млн. руб.
А %2001=1,28 млн. руб.
Все перечисленные показатели динамики оформляем в итоговую таблицу.
Таблица 7.2.
Показатели динамики производства продукции предприятия
за 1996-2001гг.
|
Год |
Произв-во продукции, млн. руб. |
Абсолютные приросты, млн. руб. |
Темпы роста, % |
Темпы прироста, % |
Абсолют. значение 1% прироста, тыс. руб. |
|||
|
цепные (ежегод.) |
базисные (к 1996г.) |
цепные (ежегод.) |
базисные (к 1996г.) |
цепные (ежегод.) |
базисные (к 1996г.) |
|||
|
А |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1996 1997 1998 1999 2000 2001 |
101 108 110 117 122 128 |
– 7 2 7 5 6 |
– 7 9 16 21 27 |
– 106,9 101,8 106,4 104,3 104,9 |
– 106,9 108,9 115,8 120,8 126,7 |
– 6,9 1,8 6,4 4,3 4,9 |
– 6,9 8,9 15,8 20,8 26,7 |
– 1010 1080 1100 1170 1220 |
-
Средний абсолютный прирост определяется двумя способами:
а) как средняя арифметическая простая (через сумму цепных абсолютных приростов):
Δ![]() =
=![]() =
=![]() =5,4
млн. руб.,
=5,4
млн. руб.,
где n – число цепных абсолютных приростов;
б) как отношение базисного прироста к числу периодов:
Δ![]() =
=![]() =
=![]() ,
,
где n – число периодов, включая базисный;
Δ![]() =
=![]() =
=![]() =5,4
млн. руб.
=5,4
млн. руб.
-
Среднегодовой темп роста исчисляется по формуле средней геометрической из цепных коэффициентов роста:
=![]() =
=![]() ,
,
где n – число цепных темпов роста;
П – знак произведения;
=![]() =
=![]() =1,048
или 104,8 %.
=1,048
или 104,8 %.
Мы знаем правило взаимосвязи цепных и базисных темпов роста: произведение цепных темпов равно базисному темпу. Поэтому среднегодовой темп роста может быть исчислен из отношения конечного (уn) и базисного (yo) уровней по формуле:
=![]() ,
,
где m – число периодов, включая базисный;
=![]() =
=![]() =1,048
или 104,8 %
=1,048
или 104,8 %
Среднегодовой темп роста за 1996-2001гг. равен 104,8 %.
Среднегодовой темп прироста исчисляется следующим образом:
Δ = % – 100%=104,8–100=4,8%.
Таким образом, производство продукции за период 1996-2001гг. увеличивалось за год в среднем на 4,8%.
-
В нашем примере мы имеем интервальный ряд динамики с равными интервалами. Поэтому среднегодовое производство продукции исчислим по формуле средней арифметической простой:
![]() =
=![]() =
=![]() =
=![]() =114,3
млн. руб.,
=114,3
млн. руб.,
где у – уровни ряда
n – число уровней ряда.
-
Построим график производства продукции предприятия за 1996-2001гг.
у
годы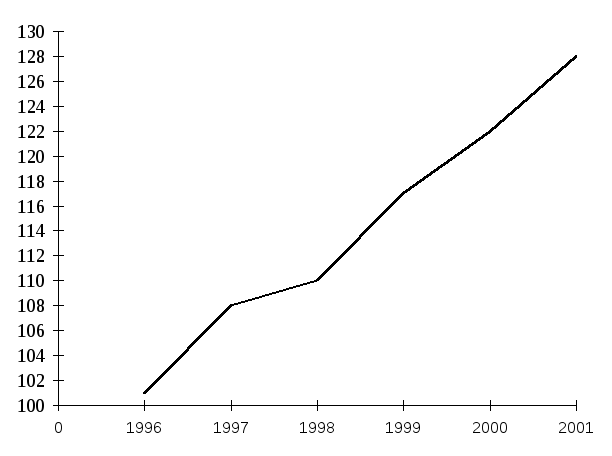
Рис. 7.1. График производства продукции предприятия за 1996-2001гг.
Важным направлением в исследовании закономерностей динамики социально-экономических явлений и процессов является изучение общей тенденции развития (тренда). Для того, чтобы отчетливее выявить тенденцию в развитии того или иного явления, применяют несколько способов обработки рядов динамики. Наиболее распространенными и простейшими методами являются:
-
укрупнение интервалов в рядах динамики;
-
метод скользящей средней;
-
аналитическое выравнивание ряда динамики.
Метод укрупнения интервалов применяется для выявления тренда в рядах динамики колеблющихся уровней, затушевывающих основную тенденцию развития. Главное в этом методе заключается в преобразовании первоначального ряда динамики в ряды более продолжительных периодов (месячные в квартальные, квартальные в годовые и т.д.).
Пример 4. Имеются данные о производстве магнитофонов за 2001 год, тыс. штук:
январь – 3,1 июль – 2,9
февраль – 1,8 август – 3,4
март – 2,6 сентябрь – 3,1
апрель – 1,6 октябрь – 3,5
май – 2,6 ноябрь – 3,3
июнь – 4,5 декабрь – 4,8
Решение: Различные направления изменений по отдельным месяцам уровней данного ряда динамики затрудняют выводы об основной тенденции производства магнитофонов. Решение этой задачи упрощается, если соответствующие месячные уровни объединить в квартальные, то есть укрупнить интервалы до трех месяцев:
I квартал – 7,5 тыс. шт.
II квартал – 8,7 тыс. шт.
III квартал – 9,4 тыс. шт.
IV квартал – 11,6 тыс. шт.
После укрупнения интервалов основная тенденция роста производства магнитофонов стала очевидной, тыс. шт.:
7,5<8,7<9,4<11,6.
Метод скользящей средней. В основу этого метода положено определение по исходным данным теоретических уровней, в которых случайные колебания погашаются, а основная тенденция развития выражается в виде некоторой плавной линии.
Пример 5. Используя пример 4, провести сглаживание ряда динамики шестимесячными скользящими средними.
Решение: Средние уровни ряда:
за январь – июнь
![]() 1
=
1
=
![]() =
=![]() =2,7
тыс. шт.
=2,7
тыс. шт.
за февраль – июль
![]() 2
=
2
=
![]() =
=![]() =2,9
тыс. шт.
=2,9
тыс. шт.
за март – август
![]() 3
=
3
=
![]() =
=![]() =2,93
тыс. шт.
=2,93
тыс. шт.
за апрель – сентябрь
![]() 4
=
4
=
![]() =
=![]() =3,1
тыс. шт. и т.д.
=3,1
тыс. шт. и т.д.
Результаты расчета шестимесячной скользящей средней представим в таблице.
Таблица 7.3.
Динамика производства магнитофонов
за шесть месяцев 2001г., тыс. шт.
|
Месяц |
Производство по месяцам, тыс. шт. yi |
Скользящие шестимесячные суммы Σ yi |
Шестимесячные скользящие средние (Σ yi)/n |
|
А |
1 |
2 |
3 |
|
январь |
3,1 (у1) |
– |
– |
|
февраль |
1,8 (у2) |
– |
– |
|
март |
2,6 (у3) |
– |
– |
|
апрель |
1,6 (у4) |
16,2 (у1+ у2+ у3+у4+ у5 +у6) |
2,7 ( |
|
май |
2,6 (у5) |
17,3 (у2+ у3+у4+ у5 +у6+у7) |
2,9 ( |
|
июнь |
4,5 (у6) |
17,6 (у3+у4+ у5 +у6+у7+у8) |
2,93 ( |
|
июль |
2,9 … |
18,1 … |
3,1 ( |
|
август |
3,4 … |
19,6 … |
3,3 … |
|
сентябрь |
3,1 … |
20,7 … |
3,4 … |
|
октябрь |
3,5 … |
21,0 (у7+у8+…+уn) |
3,5 ( |
|
ноябрь |
3,3 … |
– |
– |
|
декабрь |
4,8 (уn) |
– |
– |
В результате обработки ряда динамики методом скользящей средней появилась тенденция к росту производства магнитофонов.
тыс.шт.
месяц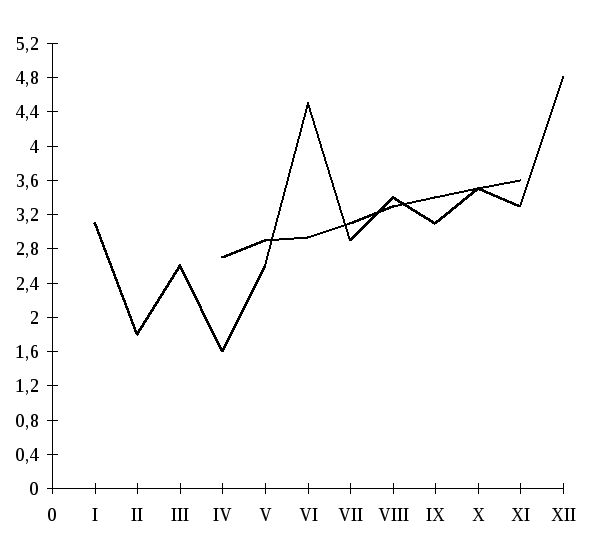

Рис. 7.2. Производство магнитофонов по месяцам в 2001 году.
Из графика тоже отчетливо видна тенденция роста производства магнитофонов.
Аналитическое выравнивание ряда динамики. Одним их условий обоснованного применения метода аналитического выравнивания в анализе рядов динамики является знание типов развития социально-экономических явлений во времени, их основных отличительных признаков.
Аналитическое выравнивание фактических уровней ряда динамики может быть проведено по прямой или какой-либо другой линии (параболе второго, третьего и т.д. порядков; гиперболе), выражающей функциональную зависимость уровней ряда динамики от времени.
Если изучаемое явление развивается равномерно, выравнивание производят по прямой линии, если абсолютные приросты по периодам изменяются (замедляются или ускоряются), то подбирают более сложную кривую.
Рассмотрим, как производится выравнивание по прямой линии.
Уравнение прямой может быть выражено в виде следующей формулы:
yt =ao+a1t,
где yt – значение выравненного ряда;
ao, a1 – параметры прямой линии (которые необходимо вычислить);
t – показатель времени.
Задача состоит в том, чтобы фактические уровни ряда (у) заменить теоретическими (yt).
Для расчета параметров прямой линии ao и a1 используем способ наименьших квадратов, который дает систему двух уравнений:
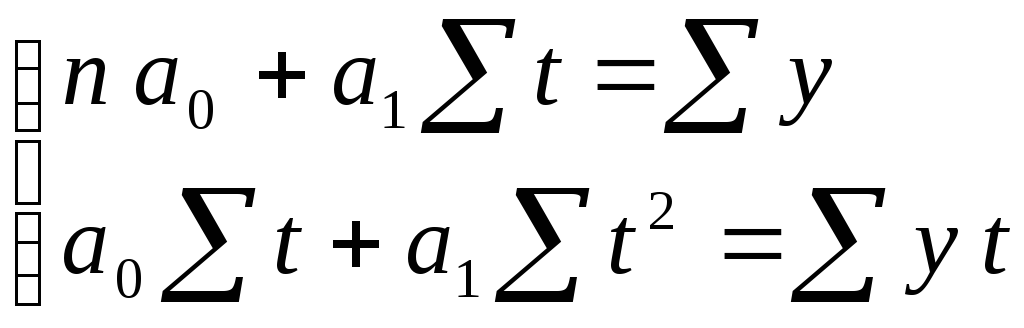 ,
,
где n – число членов ряда;
у – фактические уровни ряда;
t – показатель времени.
Дано указание: Если t являются показателями времени, то им всегда можно дать такие значения (условно), чтобы их сумма была равна нулю (Σ t = 0).
Пример 6. По данным примера 4 произвести аналитическое выравнивание и построить график.
Решение: Уравнение прямой имеет вид:
yt =ao+a1t.
Для нахождения параметров прямой решаем систему нормальных уравнений:
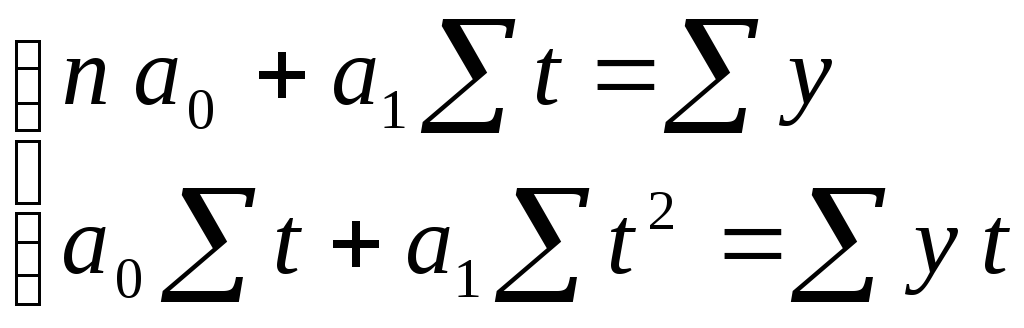 ,
,
Для решения системы строим расчетную таблицу 7.4.
Таблица 7.4.
Расчетные данные для определения параметров системы нормальных уравнений и выравненных теоретических значений (yt)
|
Месяц |
Произв-во магнитофонов, тыс. шт. |
t |
t 2 |
yt |
yt |
|
А |
1 |
2 |
3 |
4 |
5 |
|
январь февраль март апрель май июнь июль август сентябрь октябрь ноябрь декабрь |
3,1 1,8 2,6 1,6 2,6 4,5 2,9 3,4 3,1 3,5 3,3 4,8 |
-6 -5 -4 -3 -2 -1 1 2 3 4 5 6 |
36 25 16 9 4 1 1 4 9 16 25 36 |
-18,6 -9,0 -10,4 -4,8 -5,2 -4,5 2,9 6,8 9,3 14,0 16,5 28,8 |
2,26 2,4 2,54 2,68 2,82 2,96 3,24 3,38 3,52 3,66 3,8 3,94 |
|
Итого: |
Σy=37,2 |
Σ t = 0 |
Σ t 2=182 |
Σ yt=25,8 |
Σ yt=37,2 |
Так как Σ t = 0, то система нормальных уравнений примет вид:
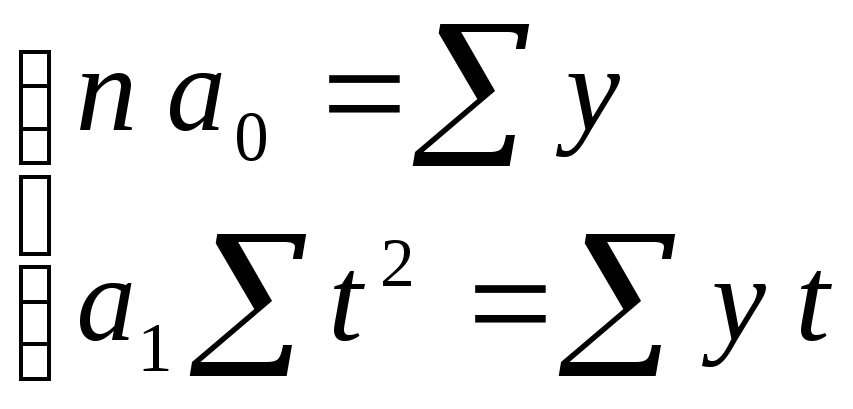 ,
,
отсюда:
ao
=
![]() =
=
![]() = 3,1 тыс. шт.;
= 3,1 тыс. шт.;
a1
=
![]() =
=
![]() = 0,142 тыс. шт.
= 0,142 тыс. шт.
Уравнение прямой будет иметь вид:
yt = 3,1+0,142 t.
Подставив в это уравнение значения t (табл. 7.4. гр. 2), получим выравненные теоретические значения yt (табл. 7.4. гр. 5).
После решения уравнения наносим на график фактические уровни и исчисленную прямую линию, характеризующую тенденцию динамического ряда.
тыс.
шт.
месяц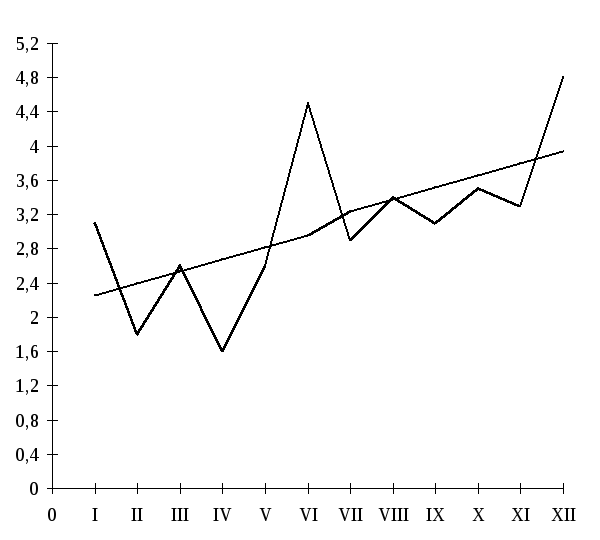

Рис. 7.3. Динамика производства магнитофонов по месяцам.
Повседневная жизнедеятельность людей в условиях периодической сменяемости сезонов сопровождается специфическими изменениями интенсивности динамики социально-экономических процессов. Поэтому студентам следует изучить еще один вопрос в этой теме – о сезонных колебаниях.
Сезонные колебания – это сравнительно устойчивые внутригодичные колебания, то есть когда из года в год в одни месяцы уровень явления повышается, а в другие – снижается. Они обуславливаются специфическими условиями, влиянием многочисленных факторов, в том числе и природно-климатических.
Перед статистикой стоит задача – выявить колебания и измерить их. Наличие сезонных колебаний выявляют с помощью графического метода. В этом случае применяют линейные диаграммы, на которые наносят данные об объеме явления по месяцам не менее чем за три года.
Измеряются сезонные колебания при помощи особых показателей, которые называются индексами сезонности. Для исчисления индексов сезонности применяют различные методы, выбор которых зависит от характера общей тенденции ряда динамики. Если ряд динамики не содержит ярко выраженной тенденции развития, то индексы сезонности исчисляют непосредственно по эмпирическим данным без их предварительного выравнивания. Для расчета индексов сезонности необходимо иметь помесячные данные минимум за три года.
Для каждого месяца рассчитывается
средний уровень (![]() i),
затем исчисляется среднемесячный
уровень для всего анализируемого ряда
(
i),
затем исчисляется среднемесячный
уровень для всего анализируемого ряда
(![]() ).
По этим данным определяется индекс
сезонности (Is)
как процентное отношение средних для
каждого месяца к общему среднемесячному
уровню ряда:
).
По этим данным определяется индекс
сезонности (Is)
как процентное отношение средних для
каждого месяца к общему среднемесячному
уровню ряда:
Is=![]() ,
,
где
![]() i
– среднемесячные уровни ряда (по
одноименным месяцам);
i
– среднемесячные уровни ряда (по
одноименным месяцам);
![]() – общий средний уровень ряда (постоянная
средняя).
– общий средний уровень ряда (постоянная
средняя).
Пример 7. Реализация картофеля на рынках города за три года характеризуется следующими данными, т:
|
Год |
Месяц |
|||||||||||
|
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
XI |
XII |
|
|
1999 2000 2001 |
71 73 65 |
72 83 60 |
80 84 59 |
180 280 260 |
280 350 335 |
474 434 485 |
295 260 310 |
107 86 132 |
608 628 650 |
610 480 520 |
185 178 187 |
105 168 103 |
Определить индексы сезонности.
Решение: Применяя формулу средней арифметической простой, определим среднемесячные уровни за три года:
![]() i
=
i
=![]() ,
,
январь:
![]() 1
=
1
=
![]() =
=
![]() = 69,7 т;
= 69,7 т;
февраль:
![]() 2
=
2
=
![]() =
=
![]() = 71,7 т;
= 71,7 т;
март:
![]() 3
=
3
=
![]() =
=
![]() = 74,3 т и т.д.
= 74,3 т и т.д.
(см. табл. 7.5., гр. 5).
Таблица 7.5.
Реализация картофеля на рынках города
за три года, т
|
Месяц |
|
|
|
|
|
Индекс сезонности (Is), % |
|
1999г. |
2000г. |
2001г. |
Сумма за три года |
Средне-месячная
за три года,
|
||
|
А |
1 |
2 |
3 |
4 |
5 |
6 |
|
январь февраль март апрель май июнь июль август сентябрь октябрь ноябрь декабрь |
71 72 80 180 280 474 295 107 608 610 185 105 |
73 83 84 280 350 434 260 86 628 480 178 168 |
65 60 59 260 335 485 310 132 650 520 187 103 |
209 215 223 720 965 1393 865 325 1886 1610 550 376 |
69,7 71,7 74,3 240 321,7 464,3 288,3 108,3 628,7 536,7 183,3 125,3 |
26,9 27,6 28,6 92,5 124,0 179,0 111,1 41,7 242,4 206,9 70,7 48,3 |
|
Итого |
3067 |
3104 |
3166 |
9337 |
259,4 |
100,0 |
Исчислим общую среднюю (постоянную):
![]() =
=![]() ,
,
![]() =
=![]() =259,4
или
=259,4
или
![]() =
=![]() =
=![]() =
=![]() =259,4
т
=259,4
т
Теперь можно рассчитывать индексы сезонности:
январь: Is=![]() =0,269
или 26,9%,
=0,269
или 26,9%,
февраль: Is=![]() =0,276
или 27,6%,
=0,276
или 27,6%,
март: Is=![]() =0,286
или 28,6% и т.д.
=0,286
или 28,6% и т.д.
(см. табл. 7.5., гр. 6)
Индексы сезонности показывают, что наименьший спрос приходится на январь-февраль, а наибольший – на сентябрь-октябрь.
Для наглядности построим график сезонной волны реализации картофеля (рис. 7.4.).
Is,
%
IS месяц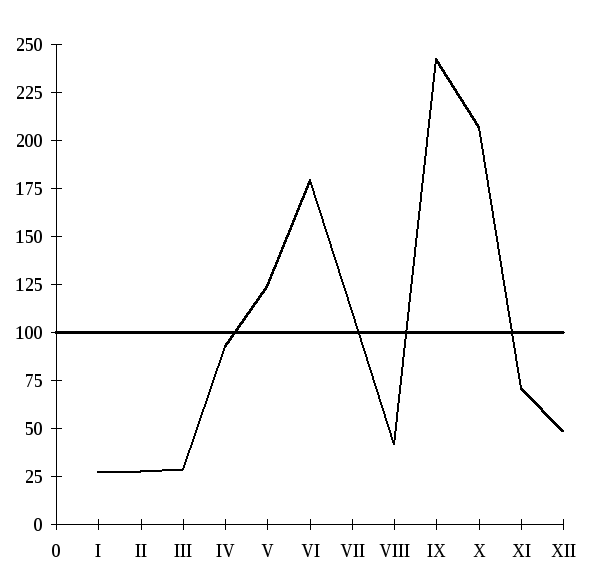

Рис. 7.4. Сезонная волна реализации картофеля (изменение индексов сезонности в среднем за три года).
