Тема 6. Показатели вариации.

В ходе анализа средних величин возникает вопрос о степени колеблемости признака. Необходимость изучения вариации вызывается тем, что на величине средней отражаются лишь общие условия, присущие данной совокупности, и не находят отражения индивидуальные особенности, порождающие вариацию признака у отдельных единиц совокупности. Исследование вариации является необходимым звеном в анализе экономических явлений и процессов. Показатели вариации служат вместе с тем и характеристикой типичности самой средней.

Студентам необходимо понять смысл и изучить методику расчета различных показателей вариации: размаха вариации, среднего линейного отклонения, среднего квадратического отклонения и коэффициента вариации. Размах вариации:

R = х_max – х_min,

где х_max, х_min – максимальное и минимальное значение признака.

Размах вариации дает только общее представление о колеблемости признака, но не показывает, как колеблется признак внутри совокупности.

Среднее линейное отклонение () определяется по формулам:

1. для несгруппированных данных (первичного ряда)

= ;

2. для n вариационного ряда

= .

Среднее квадратическое отклонение (σ) рассчитывается по слеующей формуле:

σ = .

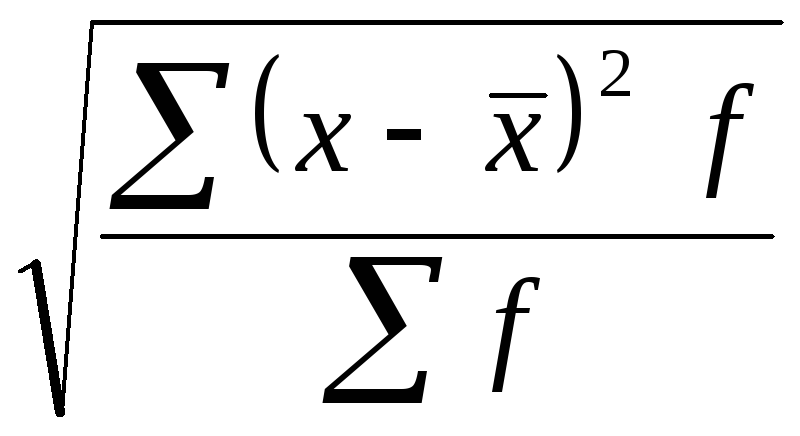Среднее квадратическое отклонение является абсолютной мерой вариации признака в совокупности и выражается в тех же единицах измерения варьирующего признака.

Пример 1. По данным выборочного обследования произведена группировка вкладчиков по размеру вклада в Сбербанке города:

Размер вклада, руб.	До 400	400-600	600-800	800-1000	Св. 1000
Число вкладчиков	32	56	120	104	88

Определить средний размер вклада и среднее квадратическое отклонение.

Решение: Для расчета среднего размера вклада и среднего квадратического отклонения строим расчетную таблицу 6.1.

Таблица 6.1.

Расчет среднего квадратического отклонения

Группы вкладчиков по размеру вклада, руб.	Число вкладчи-ков	x	xf		()2	()2 f
А	Б	1	2	3	4	5
До 400 400-600 600-800 800-1000 св. 1000	32 56 120 104 88	300 500 700 900 1100	9600 28000 84000 93600 96800	-480 -280 -80 +120 +320	230400 78400 6400 14400 102400	7372800 4390400 768000 1497600 9011200
Итого	400	–	312000	–	–	23040000

Определим средний размер вклада:

= = = 780 руб.

Определим среднее квадратическое отклонение:

σ = = 240 руб.

Дисперсия признака (σ²) – это средняя арифметическая квадратов отклонений отдельных значений признака от их средней арифметической:

σ² = = 57600.

Для сравнения размеров вариации различных признаков, а также для сравнения степени вариации одноименных признаков в нескольких совокупностях исчисляется относительный показатель вариации – коэффициент вариации (V), который представляет собой процентное отношение среднего квадратического отклонения к средней арифметической:

V = .

По величине коэффициента вариации можно судить о степени вариации признаков, а следовательно, об однородности состава совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, тем менее однородна совокупность по составу:

V = = 30,8%.

Небольшая колеблемость признака, то есть средний вклад 780 руб., – реальная величина и может представлять данную группу вкладчиков по размеру вклада.

Расчет среднего квадратического отклонения представляет собой трудоемкую операцию. Эти расчеты можно значительно упростить, если применить способ отсчета от условного нуля, то есть способ «моментов».

Суть способа «моментов» заключается в том, что:

1. из всех вариант вычитается постоянное число «А» (значение серединной варианты или варианты, имеющей наибольшую величину);

2. все варианты делятся на постоянное число, а именно: на величину интервала (i).

Получаем новую среднюю, которая называется моментом первого порядка (m₁):

m₁ =,

тогда средняя арифметическая будет равна =

Для расчета среднего квадратического отклонения находим момент второго порядка (m₂):

m₂ = ,

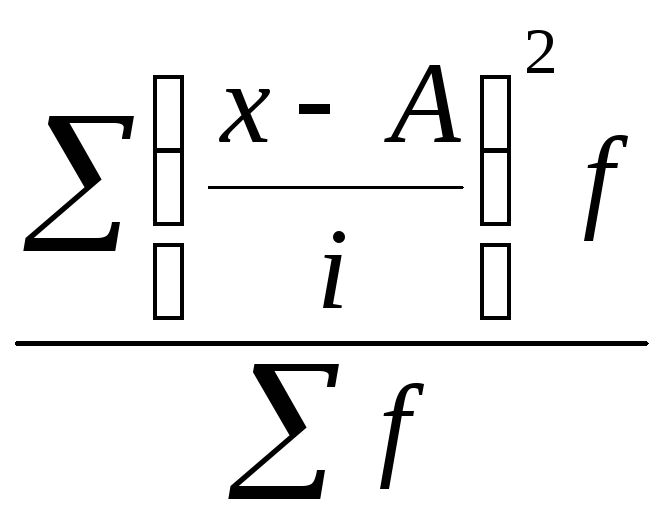и среднее квадратическое отклонение будет равно:

σ = i

Пример 2. Рассмотрим расчет среднего квадратического отклонения способом «моментов», используя данные примера 1.

Таблица 6.2.

Расчет среднего квадратического отклонения

способом «моментов»

Группы вкладчиков по размеру вклада, руб	Число вкладчи-ков	x	x-А
А	Б	1	2	3	4	5	6
До 400 400-600 600-800 800-1000 св. 1000	32 56 120 104 88	300 500 700 900 1100	-400 -200 0 +200 +400	-2 -1 0 1 2	-64 -56 0 104 176	4 1 0 1 4	128 56 0 104 352
Итого:	400	–	–	–	160	–	640

А = 700 по наибольшей частоте

i = 200

m₁ = = 0,4;

= = 780 руб.

Средний размер вклада составил 780 руб.

m₂ = = 1,6

σ = 200 = 200 = 240 руб.

Получим тот же результат, что и в примере 1.