ekonomika_promishlennosti / Uchebnoe posobie Ekonomika energetiki NDRogalev MEI 2005.pdf / Учебное пособие Экономика энергетики Н.Д.Рогалёв МЭИ 2005

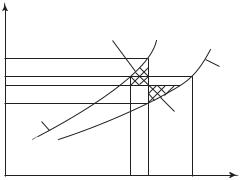
Рис. 9.15. Определение наивыгоднейшего числа работающих агрегатов:

А — пуск или останов 2-го агрегата; Б — 3-го агрегата; В — 4-го агрегата; ∆Р — потери мощности; Р — нагрузка гидростанции

Эти потери складываются из потерь в турбинах, гидрогенераторах и водопроводящих сооружениях. С повышением нагрузки ГЭС критерием перехода от работы z гидроагрегатов к (z + 1) гидроагрегатам является равенство суммарных потерь мощности (имеются и другие способы определения искомых нагрузок).

Характеристика относительных приростов расхода воды гидроагрегата rга = f (Pа) представляет собой зависимость относительного прироста расхода воды от его электрической нагрузки.

Характеристика относительных приростов расхода воды гидростанцией строится суммированием характеристик отдельных гидроагрегатов при одинаковых значениях относительных приростов расхода воды.

Поскольку на гидростанции в большинстве случаев устанавливаются однотипные агрегаты, то суммирование заменяется умножением расхода воды одним агрегатом на число агрегатов при неизменной мощности.

При данном числе включенных в работу агрегатов ГЭС (меньшем максимального количества) с ростом электрической нагрузки относительный прирост расхода воды постепенно увеличивается. Если при данной электрической нагрузке гидростанции ввести в работу дополнительный гидроагрегат, то нагрузка на каждом гидроагрегате снизится и уменьшится относительный прирост расхода воды ГЭС.

181

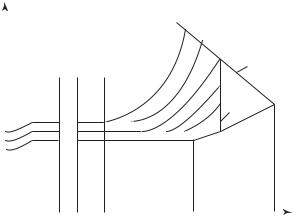
Рис. 9.16. Характеристика относительных приростов расхода воды гидростанции:

rг — относительный прирост расхода воды; Р — нагрузка гидростанции

Этому на рис. 9.16 соответствует переход от относительного прироста rг1 к rг2 при нагрузке Р1. Следовательно, суммарная характеристика относительных приростов расхода воды на ГЭС при переменном количестве работающих агрегатов имеет пилообразный характер с разрывами непрерывности при нагрузках, соответствующих включению (отключению) каждого агрегата (см. на рис. 9.16 — ломаная линия А — Б — В — Г). Использование такой характеристики практически затруднено из-за неоднозначности величины электрической нагрузки ГЭС при данном значении относительного прироста расхода воды. Так, при относительном приросте rг3 имеются два значения электрической нагрузки: Р2 и Р3. Поэтому характеристику относительных приростов ГЭС сглаживают.

Характеристика сглаживания. Распределение нагрузки производится для электростанций, работающих в одной зоне графика нагрузки. Так как ГЭС работают в другой зоне нагрузки по сравнению с остальными станциями энергосистемы, то переход от z к (z + 1) агрегатам не вызывает изменения относительного прироста расхода топлива на тепловых электростанциях энергосистемы. Поэтому при таком сглаживании можно руководствоваться только характеристикой рассматриваемой ГЭС и не учитывать характеристик остальных станций энергосистемы. Тогда искомое значение относительного прироста должно быть выбрано таким, чтобы расход воды, подсчитанный по действительной и сглаженной характеристикам, не изменился. Этому

182

условию соответствует значение относительного прироста rг4 (см. рис. 9.16), при котором площадь F1 (снижение расхода воды по сравнению с действительной характеристикой) равна площади F2 (повышение расхода воды по сравнению с действительной характеристикой). Сглаженная характеристика относительных приростов расхода воды при переходе от z к (z + 1) гидроагрегату представлена на рис. 9.16 ломаной линией А — Д — Е — Г. Производя аналогичные построения для каждого дополнительного вводимого в работу гидроагрегата, получаем характеристику относительных приростов ГЭС при данном напоре Н.

Представленная на рис. 9.16 сглаженная характеристика относительных приростов содержит три различающихся участка:

•начальный нелинейный участок, относящийся к работе одного агрегата на ГЭС (от Рmin до Ркр.а);

•промежуточный прямолинейный участок, соответствующий

сглаженной пилообразной части характеристики ГЭС (от Ркр.а до Ркр);

• конечный криволинейный участок, относящийся к работе всех агрегатов ГЭС (от Ркр до Рmax).

Точке излома характеристики при переходе от участка Б к участку В, называемой «критической», соответствует электрическая мощность, определенная с некоторым приближением по формуле, МВт:

Ркр= Ркр.а zmax при Н = const,

где Ркр.а — критическая нагрузка одного агрегата при данном напоре, МВт; zmax — максимальное количество работающих гидроагрегатов на ГЭС.

Характеристики относительных приростов расхода воды гидростанций при различных напорах представлены на рис. 9.17.

Зависимость между критической нагрузкой ГЭС и напором может быть представлена в виде, МВт:

где Ркр max — критическая нагрузка гидроагрегата, соответствующая наибольшему напору (Нmax) ГЭС, МВт; Н — рассматриваемый напор на ГЭС; α г.кр — величина снижения критической нагрузки при уменьшении напора на 1 м, МВт/м.

Максимальная мощность ГЭС может ограничиваться мощностями турбин или генераторов (см. рис. 9.17).

183

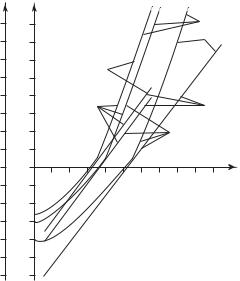
Рис. 9.17. Характеристики относительных приростов расхода воды гидростанции при различных напорах:

I — ограничение по турбинам; II — ограничение по генератору; rг — относительный прирост расхода воды; Р — нагрузка гидростанции; 1 — 6 — напор Н = 95; 97,5; 100; 102,5; 105; 107,5 м

Максимальная мощность, ограничиваемая турбинами, зависит от напора, МВт:

Рmax = (Ру max – α г max (Нmax – Н)) zmax,

где Ру max — условная максимальная мощность ГЭС, соответствующая точке пересечения экстраполированной линии ограничения мощности ГЭС по турбинам с экстраполированной характеристикой относительных приростов ГЭС при этом напоре, МВт; αг max — величина снижения максимальной мощности каждого агрегата ГЭС при уменьшении напора на 1 м, МВт/м.

Ограничение по генератору показано на рис. 9.17 вертикальной прямой.

Минимальная нагрузка ГЭС может ограничиваться неэнергетическими потребителями: расходом воды на обеспечение судоходства, ирригации, водоснабжения и др.

Характеристика относительных приростов ГЭС выражается уравнением вида, (м3/с) / МВт:

при Р > Ркр2

при Ркр1 < Р ≤ Ркр2

rг = r0 г + т1 Ркр2,

184

где r0 г — начальное значение относительного прироста расхода воды; т1 — коэффициент, отражающий наклон характеристики в зоне от минимальной нагрузки до критической при учете неустановившегося режима, связанного с быстрыми изменениями уровня нижнего бьефа ГЭС; т2, т3 — коэффициенты, отражающие конфигурацию криволинейной части характеристики.

Величина r0 г вычисляется по формуле, (м3/с)/МВт: r0 г = 102/Н ηmax,

где Н — напор, м; ηmax — максимальный КПД, отн. ед. Сопоставительные расчеты с использованием конкретных приме-

ров показали, что погрешность в относительном приросте расхода воды при использовании аналитического выражения (9.14) не превышает 5…6 %.

9.7. Расходные энергетические характеристики атомных электростанций

Характеристика расхода ядерного горючего на производство электрической продукции, выраженного в тоннах условного топлива, описывается следующей зависимостью:

В = Вх.х + rp Qp, (9.18) где Вх.х — расход топлива на покрытие потерь теплоты на холостой ход, выраженный в условном топливе, т/ч; Qp — тепловая мощность реактора, ГДж/ч; rp — относительный прирост расхода ядерного горючего реакторами, т у.т/ ГДж.

Величина rp принимается равной 0,0341 т у.т/ ГДж, т.е. без составляющей потерь. Это определяется тем, что суммарные потери в системе реактор — парогенератор на тепловое рассеивание не превосходят 0,25…0,5 % полной тепловой мощности реактора, не зависят от тепловой нагрузки и типа реактора.

Расходную характеристику машинного зала АЭС с п конденсационными турбинами можно представить в виде, ГДж/ч:

i=1

где Qх.хi — расход теплоты на холостой ход i-м турбоагрегатом, ГДж/ч; Pi — любая электрическая нагрузка i-го турбогенератора

185

(в пределах от минимальной до максимальной), МВт; Pкрi — критическая электрическая нагрузка i-го турбоагрегата, МВт; rт1i — относительный прирост расхода теплоты i-м турбоагрегатом в диапазоне от минимальной нагрузки до критической, ГДж/(МВт·ч); rт2i — то же в диапазоне от критической нагрузки до максимальной, ГДж/(МВт·ч).

Пренебрегая потерями в паропроводах и приравнивая величины Qp и Qм.з на основе уравнений (9.18) и (9.19), получаем расходную характеристику атомной электростанции, т/ч:

n

В = Вх.х + rp ∑ (Qх.х i + rт1 i Pi + (rт2 i – rт1 i) (Pi – Pкр i)). (9.20)

i=1

Вслучае использования п однотипных конденсационных турбин на АЭС уравнение (9.20) упрощается:

В= Вх.х + rp (Qх.х i + rт1 i Pi + (rт2 i – rт1 i) (Pi – Pкр i)) п.

Относительные приросты условного топлива блоком реактор— парогенератор—турбоагрегат или АЭС при однотипных турбоагрегатах можно определить по формулам, т/(МВт·ч):

rа1 = 0,0341 rт1; rа2 = 0,0341 rт2.

Расходная характеристика блока реактор—парогенератор—турбо- агрегат может быть представлена выражением, т/ч:

В = Вх.х + rа1 P + (rа2 – rа1) (P – Pкр1).

Если АЭС имеет в своем составе турбоагрегаты с разными значениями относительных приростов расхода теплоты, то характеристика относительных приростов расходов топлива АЭС имеет вид ступенчатой зависимости.

9.8. Оптимальное использование производственных мощностей электростанций в энергетической системе

Общие принципы оптимального использования производственных мощностей электростанции в энергетической системе (подход и методика) аналогичны распределению нагрузки внутри станции.

Для определения наивыгоднейшего распределения электрической нагрузки между станциями энергосистемы или между системами в объединении систем необходимо учитывать поправочные коэффициенты на изменение потерь мощности в электрической сети:

186

δ = 1/(1 − σ) ,

где σ — относительный прирост потерь активной мощности в сети для данной станции (при распределении нагрузки между станциями системы) или для данной системы (при распределении нагрузки между энергосистемами в объединении систем).

В общем случае относительный прирост потерь мощности для каждой i-й электростанции можно представить в виде

σ = P/dPi = β1Р1 + β2Р2 + …+ βiРi + …+ βпРп + А,

где Р1, Р2, …, Рi, …, Рп — электрические нагрузки 1, 2, …, i, …, п-й электростанции; ∆Р — суммарные потери активной мощности; β1, β2, ..., βi, …, βп — постоянные коэффициенты; А — величина, зависящая от нагрузок потребителей.

Аналогичное выражение может быть записано и при распределении нагрузок между системами. Следовательно, в общем случае относительный прирост потерь мощности данной электростанции (системы) зависит не только от нагрузки этой станции (системы), но и от нагрузок других станций (систем), параметров электрической сети, нагрузок потребителей.

Изменение величины относительного прироста потерь активной мощности данной электростанции (системы) в зависимости от ее нагрузки при прочих постоянных условиях представляет характеристику относительного прироста потерь мощности.

Рассмотрим характеристику относительного прироста потерь мощности на примере линии электропередачи 110 кВ, от которой питаются тяговые подстанции железнодорожного транспорта (рис. 9.18). Эта характеристика имеет вид линии, пересекающей ось абсцисс в точке, соответствующей минимуму кривой потерь мощности P = f (Р1). При увеличении активной нагрузки тяговых подстанций на транзитной линии прямая σ смещается параллельно самой себе вправо, а при увеличении напряжения на конце линии U2 — влево.

Оптимальность использования производственных мощностей энергообъединений сложной структуры, включающих электростанции различных типов с различающимися составом оборудования и видами используемых энергоресурсов, достигается при применении экономико-математических методов и ЭВМ. К ним, например, относятся: тепловые нагрузки ТЭЦ, расходы воды на ГЭС и требования неэнергетических водопользователей, ограничения по режиму использования АЭС, параметры и схемы электрических сетей, характеристики топливоснабжения и условия использования нетранспортабельных видов топлива, вторичных энергоресурсов и др.

187

Рис. 9.18. Характеристика относительных приростов потерь активной мощности и

поправочного коэффициента σ (U1 = 115 кВ, R = 52,7 Ом):

P — суммарная нагрузка линии электропередачи; Р1 — величина активной мощности, передаваемой с одного конца линии электропередачи; U1, U2 — напряжение соответственно в начале и в конце линии электропередачи; R — суммарное активное сопротивление одной фазы линии электропередачи

Впроцессе оптимизации должен решаться ряд взаимосвязанных задач:

• выбор оптимального распределения электрических нагрузок энергообъединения;

• выбор оптимального состава работающего оборудования;

• оптимальное планирование ремонтов энергооборудования;

• выбор оптимального распределения тепловых нагрузок районов теплоснабжения и др.

Внастоящее время при наличии больших энергетических систем (например, ЕЭС) в России решение этих задач возможно методом декомпозиции, применяемым при расчетах больших систем. В этом случае расчет проводится поэтапно в соответствии с иерархической структурой диспетчерского управления ЕЭС России.

Существующие методы решения рассматриваемых задач могут быть разделены на две группы:

• методы вариационного исчисления;

• оптимизационные методы математического программирования.

188

Первая группа методов исследует экстремум функционала. Им могут быть суммарный расход топлива (в тоннах условного топлива) или затраты на производство электроэнергии, зависящие от ряда функций и учитывающие непрерывное изменение показателей во времени. Экстремум функционала определяется системой дифференциальных уравнений Лагранжа.

Вторая группа методов основана на сравнении суммарных расходов топлива (в тоннах условного топлива) или денежных затрат при различных вариантах распределения электрических нагрузок или составах работающего оборудования.

При условии наивыгоднейшего распределения электрических нагрузок между электростанциями, входящими в энергообъединение в качестве критерия оптимизации рассмотрим сначала минимум расхода топлива в энергообъединении.

Условия допустимости оптимального режима использования электростанций в энергообъединении следующие.

1. Выполнение в каждый момент времени баланса мощностей энергообъединения, МВт:

где Р1, Р2, …, Рп — генерируемые активные мощности тепловых электростанций, не имеющих ограничений по расходу топлива в данный момент времени, МВт; Рп+1, …, Рт — то же для тепловых электростанций, имеющих ограничения по расходу топлива, МВт; Рг1, …, Рг п — то же для гидростанций, МВт; Ра 1, …, Ра п — то же для атомных станций, МВт; ∑Рн — суммарная активная нагрузка потребителей этих электростанций (включая расход на собственные нужды станций и сетей), МВт; ∆Р — потери активной мощности в электрической сети, МВт.

2. Обеспечение (п + 1), …, т-й тепловыми электростанциями за-

где Вп + 1, Вп + 2, …, Вт — часовые расходы условного топлива (п + 1), (п + 2), …, т-й тепловыми электростанциями, т/ч; B0 (n + 1), B0 (n + 2), …, B0т — величины ограничений по суточным расходам топлива этими же станциями.

189

3. Обеспечение использования гидростанциями заданных суточных расходов воды на энергетические нужды, м3/сут:

где Qr 1, Qr 2, …, Qr n — часовые расходы воды 1, 2, …, п-й гидростанциями на энергетические нужды, м3/ч; Q0г 1, Q0г 2, …, Q0г п — заданные суточные расходы воды этими же станциями, м3/сут.

4. Обеспечение атомными электростанциями суточной экономии органического топлива не меньше заданной, т у.т/сут:

где Ва1, Ва2, …, Вап — суточная экономия органического топлива за счет использования электроэнергии 1, 2, …, п-й атомной электростанцией, выраженная в т у.т.; B0 а1, B0 а2, …, B0 а п — величины ограничений по суточной экономии органического топлива этими же станциями.

Минимум расхода условного топлива энергообъединением находится при выполнении условий допустимости как экстремум функционала

23

∫ (B1 + В2 + … + В п + λ п + 1 Вп + 1 + λ п + 2 Вп + 2 + … + λ т Вт +

0

+ λ г1 Qг1 + … + λ гп Qгп + λ а1 Ва1 + … + λ ап Вап + λ t W) dt,

где В1, В2, …, Вп — часовые расходы условного топлива 1, 2, …, п-й тепловыми электростанциями, т/ч; λ п + 1 , λ п + 2, …, λ т, λ г1, …, λ г п, λа1,…, λа п — некоторые постоянные множители Лагранжа; λ t — множитель, являющийся функцией времени.

Продифференцируем подынтегральное выражения по переменным Р1, Р2, …, Рп, Рп +1 и т.д.: