Список рекомендуемой литературы:

Савельев И.В. Курс общей физики. – М., т.1, 1962, с. 128-133.

Матвеев А.Н. Механика и теория относительности. - М., 1976, с. 323.

Стрелков С.П. Механика. - М., 1965, с. 214-238.

Хайкин С.Э. Физические основы механики. - М., 1971, с. 446-459.

Краткая теория вопроса:

В основе всей теории гироскопа лежит закон сохранения и изменения момента импульса (момента количества движения).

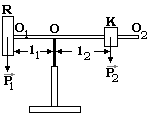
Рассмотрим гироскоп, состоящий из ротора R, который может вращаться вокруг горизонтальной оси O₁O₂ (рис. 1) и про­тивовеса K . Ось гироскопа шарнирно закреплена в точке O вер­тикальной подставки. Если противовес К расположен таким об­разом, что точка O является центром тяжести, т.е. P₁l₁ = P₂l₂,

Рис. 1

где P₁ - вес ротора, а Р₂ - вес противовеса, то результирующий момент сил, действующих на сис­тему, равен нулю .

Пусть диск вращается с уг­ловой скоростью . В этом случае он обладает моментов ко­личества движения , где J - момент инерции рото­ра относительно оси вращения. Так как на основании II закона динамики для вращательного движения: или:

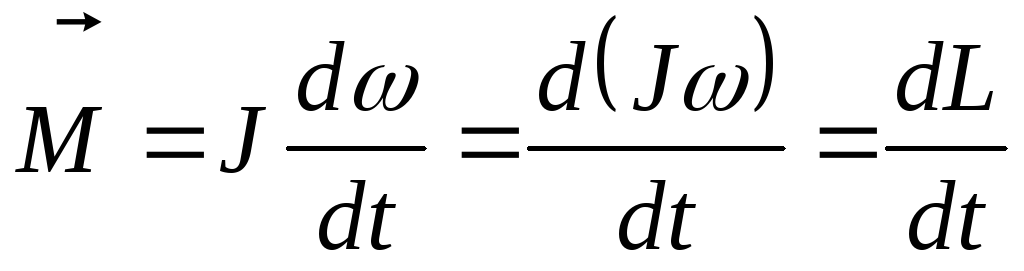, (1)

при : , то есть . Это значит, что в этом случае остается постоянным как по величине, так и по направлению, а, следовательно, ось O₁O₂, вдоль кото­рой направлен вектор , будет сохранять свое положение в пространстве неизменным.

Если переместить теперь противовес К вправо, то центр тяжести переместится в точку O` (рис.2), в результате на систему начнет действовать момент сил . В этом слу­чае .(2)

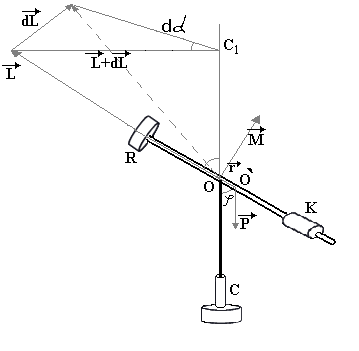
Рис. 2

Величина момента а, следовательно, и зависит как от суммарной силы тяжести, действующей на систе­му, так и от расстояния между точкой закрепления O и новым центром тяжести O`. Это расстояние определяется радиус-вектором , проведенным из точки O в O`. Согласно уравнению (2), направление вектора и вектора должны совпадать. Т.к. в этом случае вектор, а, следовательно, и оси вращения гироскопа, и тогда вектор начнет, не меняя своей величины, поворачиваться. При этом его конец будет двигаться в направлении .

В связи с тем, что вектор будет при этом все время ос­таваться перпендикулярным оси ОО`, эта ось будет все время поворачиваться, описывая конус вокруг вертикальной оси СС₁. Скорость этого вращения называется угловой скоростью прецес­сии , где - угол поворота оси гироскопа во­круг СС₁, за время .

Величина момента внешних сил (см. рис.2) рав­на или (3).

Он приложен к точке О, и перпендикулярен плоскости, преходящей через оси ОО` и СС₁.

Найдём величину скорости прецессии . Из формул (2) и (3) получим, но dL (см. рис.2) равна , тогда , откуда или .

Из последнего уравнения видно, что скорость прецессии зависит как от r , так и от скорости вращения волчка . Если  = const, то отношение должно оставаться неиз­менным при всех значениях r и равным J. Отсюда, зная  можно найти момент инерции ротора гироскопа.

Доказать самостоятельно, что r_*(P₁ + P₂) = S_*P₂ , где S - величина смещения груза Р₂ из равновесного положения, или S = l₂.

В этом случае .