3. Вынужденные колебания

3.1. Дифференциальное уравнение вынужденных колебаний и его решение

Рассмотрим теперь случай, когда в системе наряду с силами упругости и трения присутствует некоторая внешняя сила, препятствующая затуханию колебаний. Предположим, что эта вынуждающая сила F_в действует периодически с круговой частотой _в и зависит от времени по закону : F_в = F_о sin _в t , где F_о - амплитуда вынуждающей силы.

Для этого случая дифференциальное уравнение (второй закон Ньютона) имеет вид:

(13)

Сохраняя обозначения к / m =  ₀² ­, r / m = 2 , и обозначив F₀ /m = f₀ приведем уравнение (13) к виду:

(14)

Решение этого уравнения представляет некоторую функцию, которая графически представлена на рис. 3. Это решение состоит из двух частей. Одна из них соответствует неустановившемуся режиму колебаний, когда их амплитуда зависит от времени. Вторая часть описывает установившийся режим колебаний.

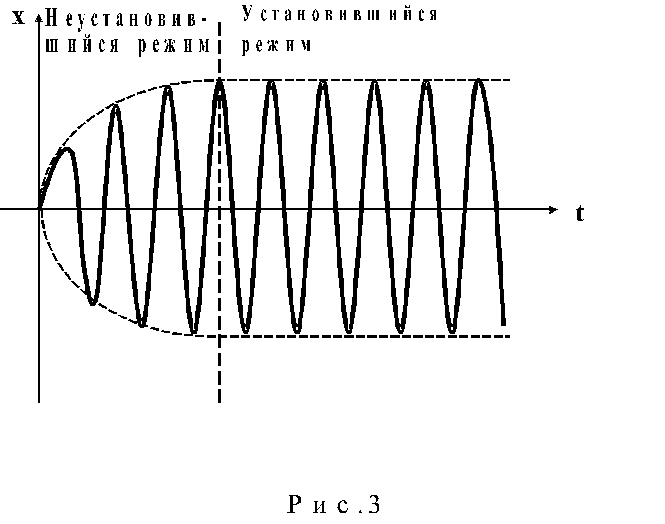
В установившемся режиме вынужденных колебаний смещение х подчиняется гармоническому закону и происходит с частотой, равной частоте действия вынуждающей силы:

х = А sin ( _в t + _o) . (15)

Установившаяся амплитуда А вынужденных колебаний, зависит от параметров системы (частоты собственных колебаний  ₀ и коэффициента затухания  ) и от характеристик вынуждающей силы (f₀ и _в): А = f (₀ , , f₀ , _в). Строгое рассмотрение приводит к следующим выражением для значений А и ₀ , входящих в формулу (15):

(16)

(17)

Из рассматриваемой формулы (16) следует, что амплитуда достигает максимального значения А_mах при определенном соотношении между величинами ₀ , _в и  .

Минимум знаменателя в формуле (16) достигается при условии:

(18)

То есть, амплитуда вынужденных колебаний максимальна, если частота действия вынуждающей силы определяется формулой (18). Явление резкого возрастания амплитуды вынужденных колебаний при частоте действия вынуждающей силы, определяемой формулой (16), называется резонансом.

Если бы затухание в системе отсутствовало ( = 0), то резонанс наступал бы при условии (₀ =  _в) и при этом амплитуда достигала бы бесконечно большого значения.

4. Сложение гармонических колебаний

Результат сложения гармонических колебаний зависит от направления складываемых колебаний, а так же от соотношения между их частотами, фазами и амплитудами. Рассмотрим на качественном уровне два случая.

4.1. Колебания проходят вдоль одной прямой с одинаковыми частотами

В этом случае складываемые колебания различаются лишь амплитудами А₁ и А₂ и начальными фазами ₀₁ и ₀₂ . Сложение таких колебаний приведет к результату:

А₁ sin ( t + ₀₁ ) + А₂ sin ( t + ₀₂ ) = А sin ( t + ₀ ) . (19)

Закон изменения смещения со временем в результирующем колебании - гармонический, частота результирующего колебания равна частоте складываемых колебаний.

Амплитуда результирующего колебания А зависит от амплитуд А₁ и А₂ , а также от разности начальных фаза ₀₁ и ₀₂ . Несложные математические вычисления позволяют выразить амплитуду А следующим образом:

(20)

Начальная фаза ₀ определяется из соотношения:

(21) Таким образом, в рассматриваемом случае результат сложения колебаний определяется формулой (19), а входящие в неё амплитуда и начальная фаза - формулами (20) и (21).