2. Затухающие колебания

2.1. Дифференциальное уравнение затухающих колебаний и его решение

В реальных системах всегда существуют некоторые силы сопротивления, препятствующие развитию колебательных процессов. Для установления характера колебательного движения в этом случае будем считать, что наряду с упругой или квазиупругой силой F_y в системе действует сила трения, пропорциональная скорости и направленная противоположно ей: F_тр = . Тогда учет влияния этих двух сил на характер движения приводит к следующему дифференциальному уравнению:

8)

Разделив левую и правую части уравнения (8) на m , обозначив r/m = 2 и сохранив обозначение к/m = ₀² , приведем это уравнение к виду:

(9)

Решение этого уравнения имеет вид:

(10)

Формула (10) представляет собой смещение при затухающем колебании как функцию времени и параметров системы  и . Коэффициент  = r/2m имеет смысл коэффициента затухания. Из формулы (10) видно, что в затухающих колебаниях амплитуда уменьшается со временем. Причем, колебания затухают тем быстрее, чем больше коэффициент затухания . По сравнению с гармоническими колебаниями уменьшается также и циклическая частота колебаний . Это уменьшение зависит от коэффициента затухания. Оказывается, что

(11)

Колебательный процесс может происходить лишь при условии: (₀² -  ²)>0, когда частота  в формуле (11) является действительной величиной . Если же затухание в системе слишком велико (₀ <  ) , то под корнем в формуле (11) оказывается отрицательная величина, - в этом случае движение не имеет периодического характера.

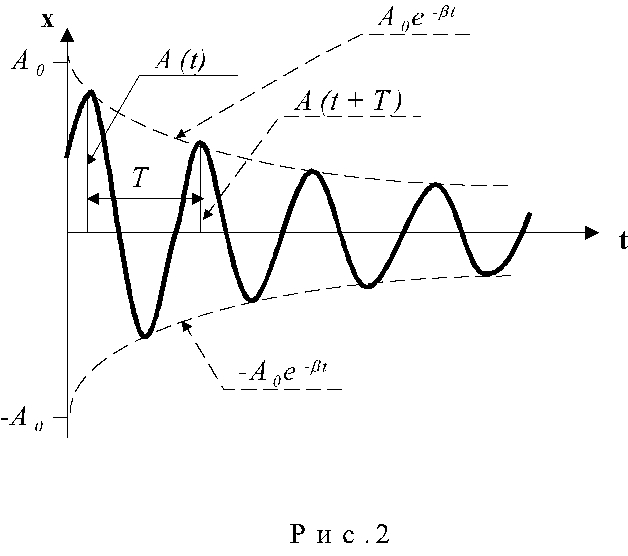
Графически затухающее колебания представлено на рис.2, где сплошной линией показана зависимость смещения от времени, а пунктирной - экспоненциальный закон убывания амплитуды.

2.2. Декремент затухания и логарифмический декремент затухания.

Уже указывалось, что быстрота убывания амплитуды затухающих колебаний характеризуется коэффициентом затухания  , который зависит от параметров системы. На практике затухание колебаний удобнее характеризовать декрементом затухания  , представляющим собой отношение двух последовательных амплитуд, разделенных периодом колебаний Т (см. рис.2) :

Натуральный логарифм этого отношения, называемый логарифмическим декрементом затухания  , весьма просто связан с коэффициентом затухания и периодом:

или  = T . (12)

Удобство использования логарифмического декремента затухания  для характеристики затухающих колебаний заключается в простоте его экспериментального определения. Если затухающие колебания зарегистрированы в виде соответствующего графика (см.рис.2), то необходимо в любых единицах измерить две амплитуды колебаний, разделенные интервалом времени, равным периоду, и найти натуральный логарифм их отношения. Определив таким образом величину  и зная период Т , легко найти и коэффициент затухания  .