
Сравнение средних значений двух нормально распределенных генеральных совокупностей.
В
медико-биологических исследованиях
актуальной является задача
сравнения выборок, полученных в результате
эксперимента, заключающегося в том
или ином воздействии на объект. Фактически
конечный результат исследования зависит
от достоверности
различий значений случайной величины
в контроле (до воздействия
или без него) и опыте (после воздействия).
Наиболее просто
решается задача определения достоверности
различий статистических
распределений, если предварительно для
выборок рассчитаны
доверительные интервалы. Положим, есть
два статистических
распределения некоторых случайных
величин X
и
У. Пусть
генеральные средние этих распределений
с доверительной вероятностью
р
=
0,95 находятся в доверительных интервалах
![]() ,
и
пусть при этом
,
и
пусть при этом
![]() .
Если соблюдается неравенство
.
Если соблюдается неравенство
![]() ,
то не вызывает сомнения, что случайная
величина Y
существенно
больше случайной величины X
(см.
рис. 3, а). Вероятность этого превышает
0,95.
,
то не вызывает сомнения, что случайная
величина Y
существенно
больше случайной величины X
(см.
рис. 3, а). Вероятность этого превышает
0,95.
На
рис. 3, б представлен вариант, когда
выборки частично пересекаются,
т. е. когда выполняется неравенство
![]() .
В
этом случае целесообразно оценивать
достоверность различий выборочных
средних хв
и
ув
с
помощью дополнительных расчетов.
Наиболее
просто это сделать, предполагая, что
случайные величины
X
и
Y
распределены
по нормальному закону. Условием
существенности
различия двух опытных распределений,
являющихся выборками
из различных генеральных совокупностей,
является выполнение
следующего неравенства для опытного и
теоретического значений
критерия Стьюдента: ton
> tTeop.
Для нахождения значения
tоп
используют следующую формулу:
.
В
этом случае целесообразно оценивать
достоверность различий выборочных
средних хв
и
ув
с
помощью дополнительных расчетов.
Наиболее
просто это сделать, предполагая, что
случайные величины
X
и
Y
распределены
по нормальному закону. Условием
существенности
различия двух опытных распределений,
являющихся выборками
из различных генеральных совокупностей,
является выполнение
следующего неравенства для опытного и
теоретического значений
критерия Стьюдента: ton
> tTeop.
Для нахождения значения
tоп
используют следующую формулу:

Здесь
![]() —
выборочные средние квадратические
отклонения,
nx
и
ny—
число вариант в выборках (объемы выборок),
—
выборочные средние квадратические
отклонения,
nx
и
ny—
число вариант в выборках (объемы выборок),
![]() и
и
![]() —
выборочные средние значения.
—
выборочные средние значения.
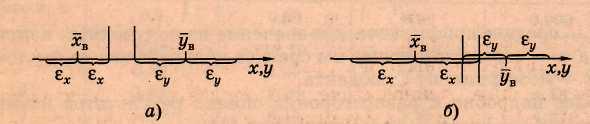
Рис.3.
