3 Решение систем уравнений: вычислительный блок Given/Find

Рассмотрим решение системы n нелинейных уравнений с m неизвестными:

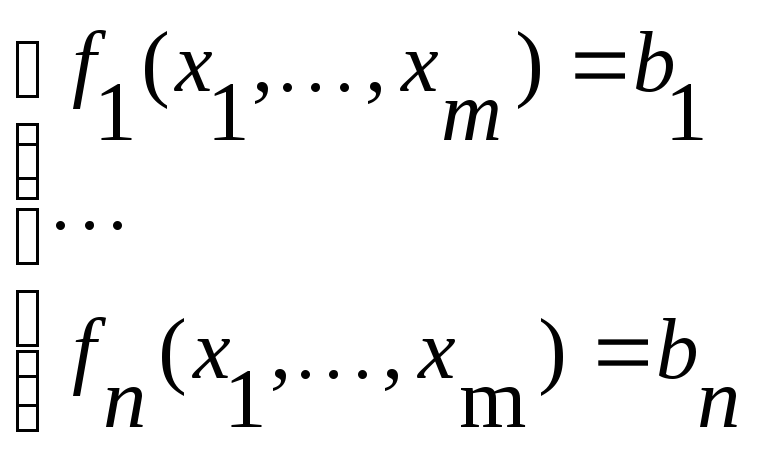
Здесь , …, – некоторые скалярные выражения, зывисящие от скалярных переменных и возможно еще каких–то переменных.

Для решения систем в MathCAD применяется специальный вычислительный блок Given/Find (Дано/Найти), состоящий из трех частей, идущих последовательно друг за другом:

1. Given – ключевое слово;

2. система, записанная логическими операторами в виде равенств и, возможно, неравенств;

3. Find(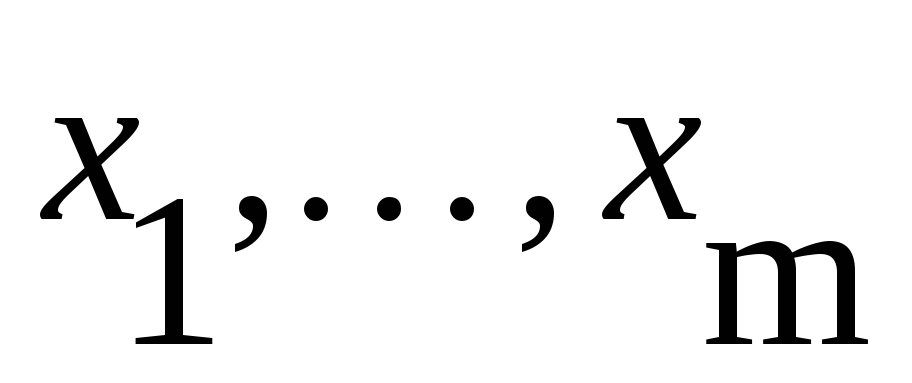) – встроенная функция для решения системы относительно переменных

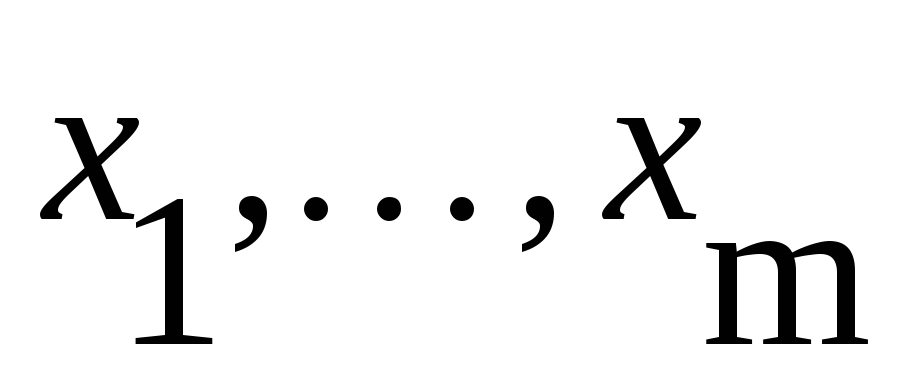
Вставлять логические операторы следует, пользуясь панелью инструментов Boolean (Булевы операторы). Блок Given/Find использует для поиска решения итерационные методы, поэтому, как и для функции root, требуется задать начальные значения всех . Сделать это необходимо до ключевого слова Given. Значение функции Find представляет собой матрицу, составленную из всевозможных решений по каждой переменной, причем количество ее строк в точности равно числу аргументов Find.

Задание: Решить систему уравнений .

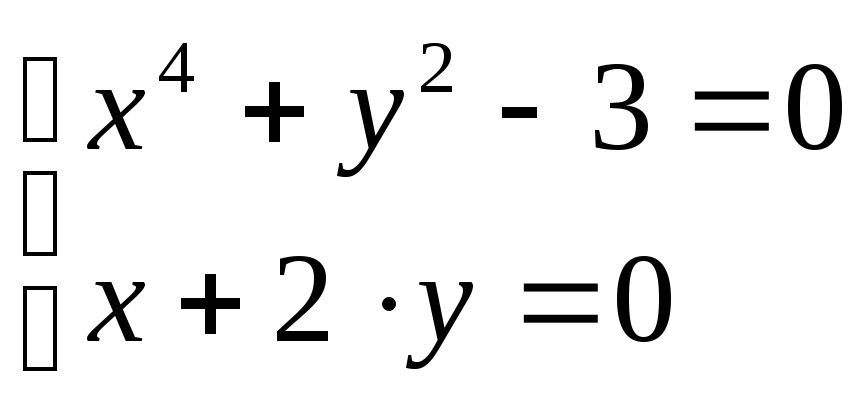Решение:

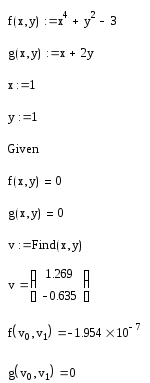
Результат: В первых двух строках вводятся функции, которые определяют систему уравнений. Затем переменным x и y, относительно которых она будет решаться, присваиваются начальные значения. После этого следует ключевое слово Given и два логических оператора, выражающих рассматриваемую систему уравнений. Завершает вычислительный блок функция Find, значение которой присваивается вектору v. В последних двух строках осуществляется проверка правильности решения системы уравнений.

Вычислительным блоком с функцией Find можно найти корень уравнения с одним неизвестным. Действия Find в этом случае совершенно аналогичны действиям в уже рассмотренном примере. Задача поиска решения рассматривается как задача решения системы, состоящей из одного уравнения. Единственным отличием будет скалярный, а не векторный тип числа, возвращаемого функцией Find.

Задание: Решить алгебраическое уравнение

Решение:

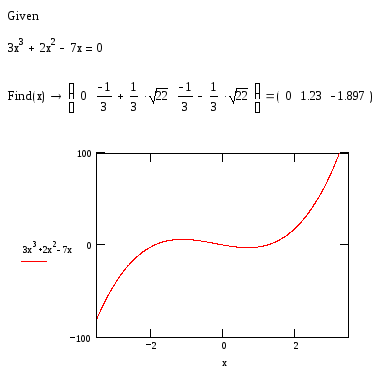
Оптимизация

1 Экстремум функции одной переменной

Задача поиска экстремума функции означает нахождение ее максимума (наибольшего значения) или минимума (наименьшего значения) в некоторой области определения ее аргументов.

Для решения задач поиска минимума или максимума в MathCAD имеются встроенные функции Minimize и Maximize. Поиск экстремума функции включает в себя задачи нахождения локального и глобального экстремумов. В MathCAD с помощью встроенных функций решается только задача поиска локального экстремума. Чтобы найти глобальный максимум (или минимум), требуется либо сначала вычислить все их локальные значения, а затем выбрать из них наибольшее (наименьшее), либо предварительно просканировать с некоторым шагом рассматриваемую область, чтобы выделить из нее подобласть наибольших (наименьших) значений функции и осуществить поиск глобального экстремума, уже находясь в его окрестности.

Для поиска локальных экстремумов имеются две встроенные функции, которые применяются как в пределах вычислительного блока, так и автономно.

1. Minimize(f, 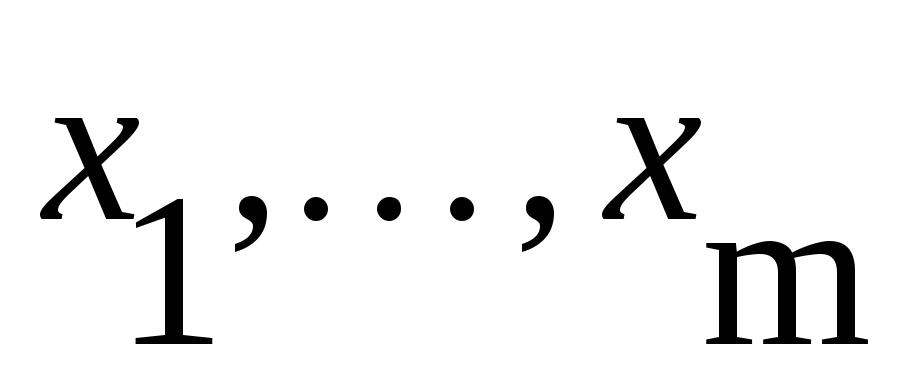) – вектор значений аргументов, при которых функция f достигает минимума

2. Maximize(f, 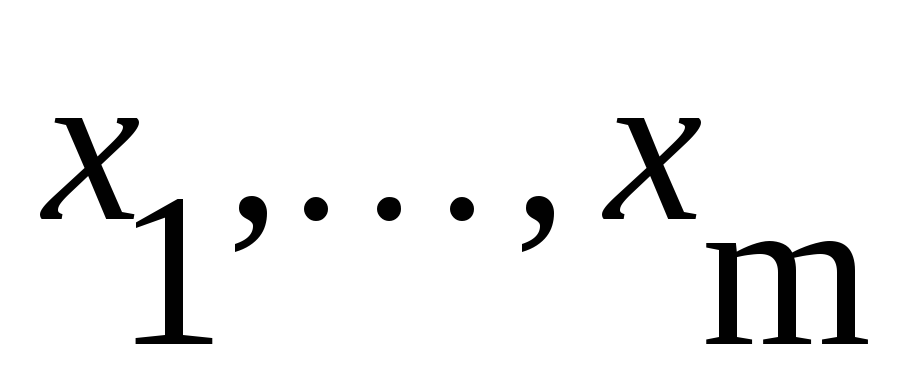) – вектор значений аргументов, при которых функция f достигает максимума, где

f() – функция,

– аргументы, по которым проводится минимизация (максимизация).

Всем аргументам функции f следует присвоить предварительно некоторые значения, причем для тех переменных, по которым проводится минимизация, они будут восприниматься как начальные приближения.

Существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются различные локальные экстремумы.

Задание: Найти минимум и максимум функции одной переменной .

Решение:

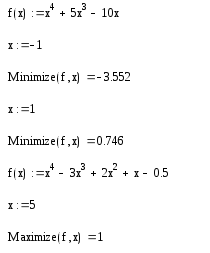
Результат: Как вы заметили, существенное влияние на результат оказывает выбор начального приближения, в зависимости от чего в качестве ответа выдаются различные локальные экстремумы.