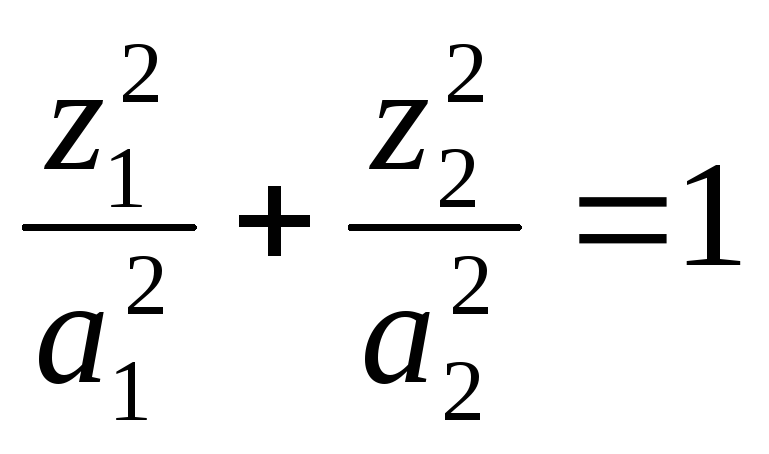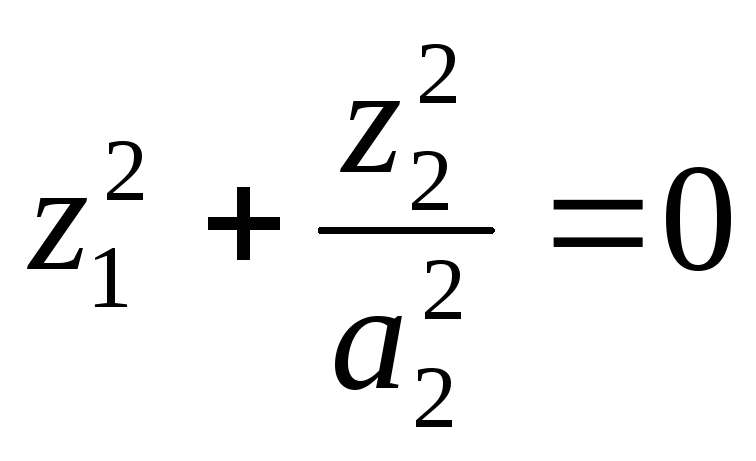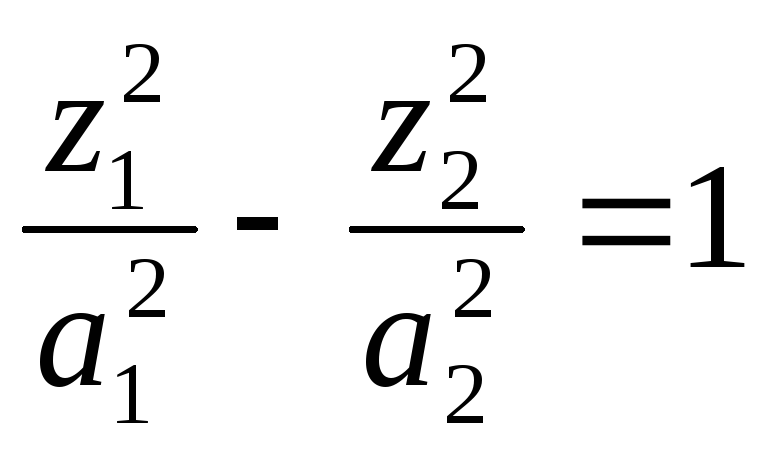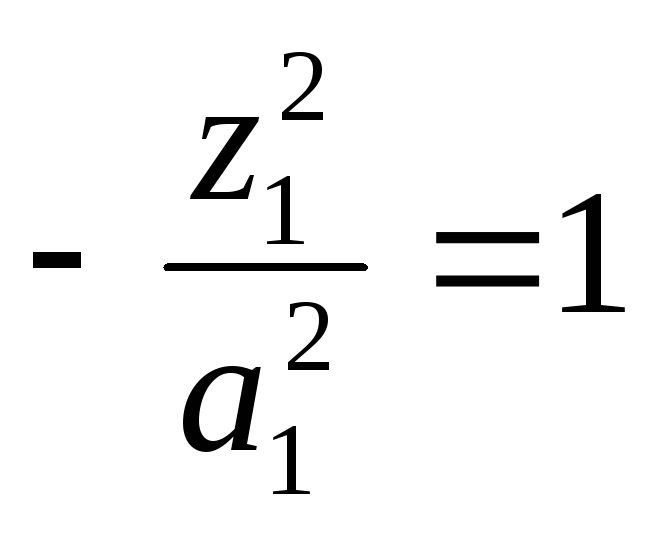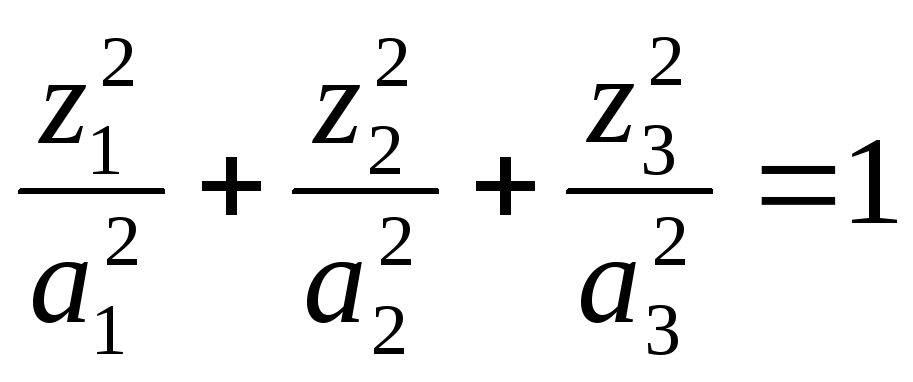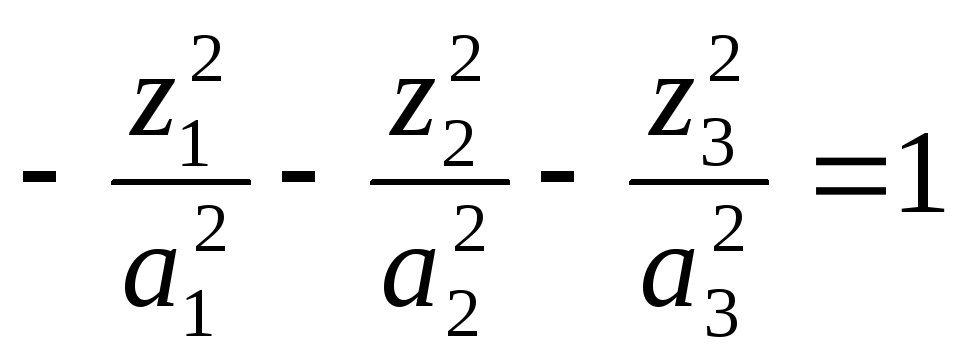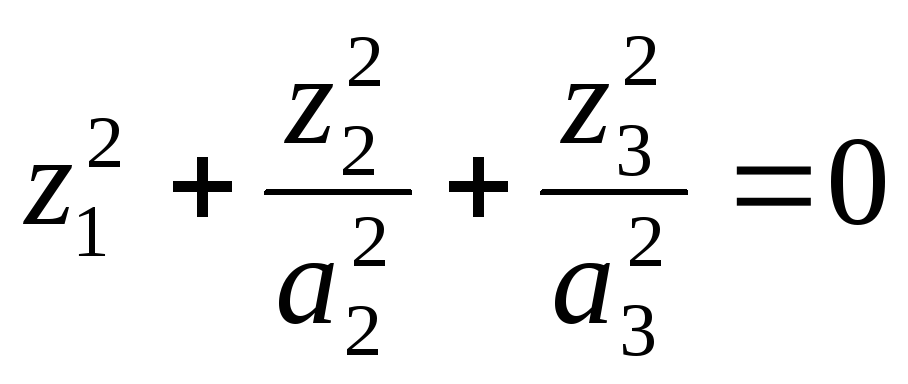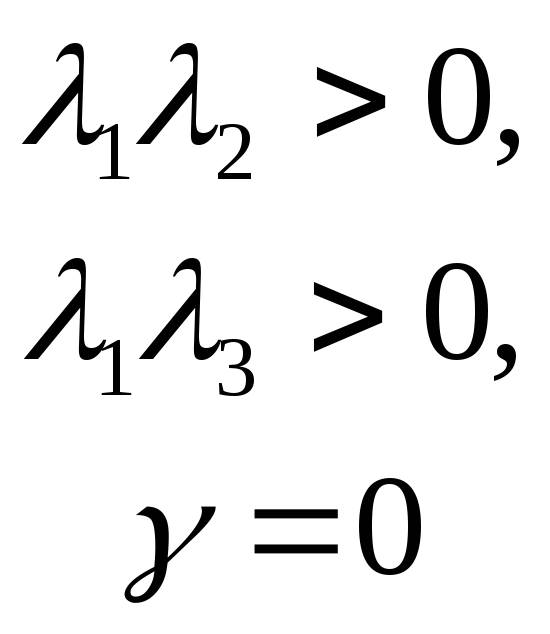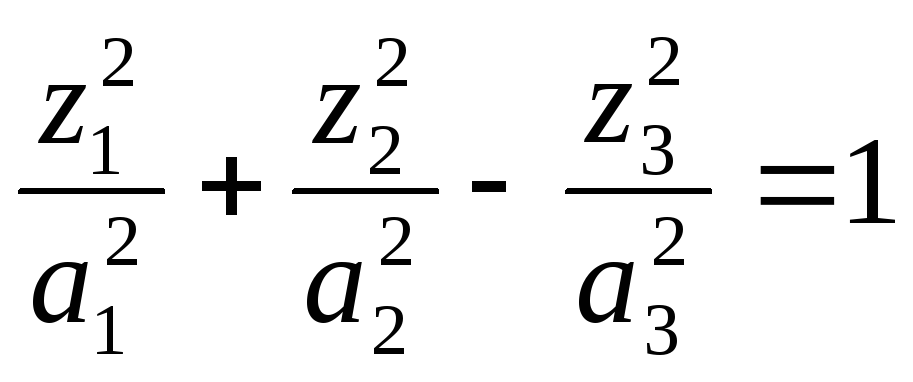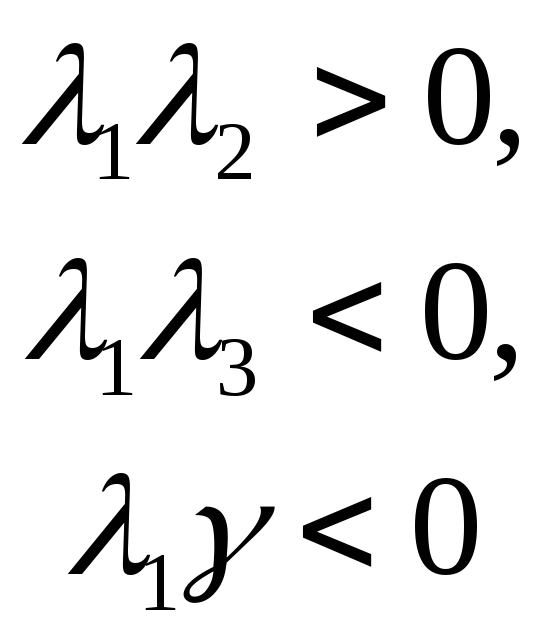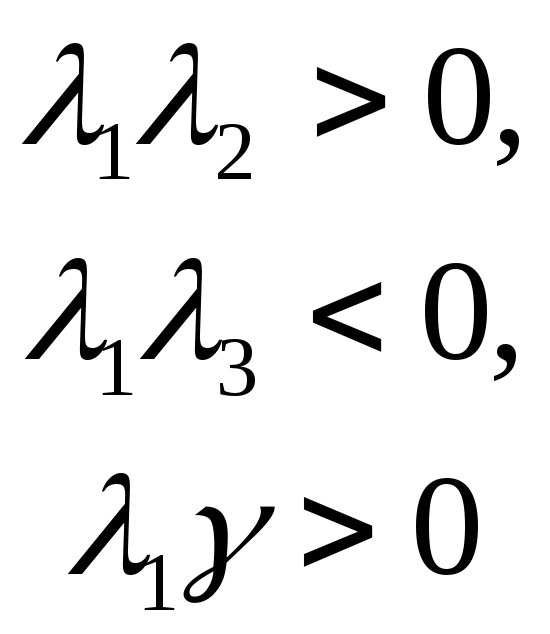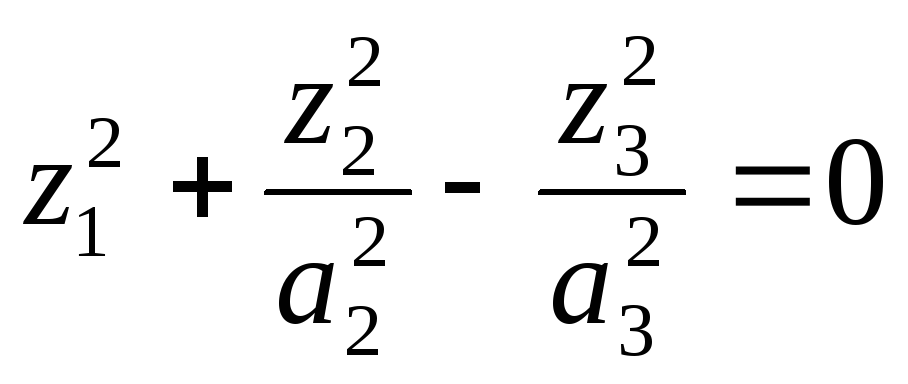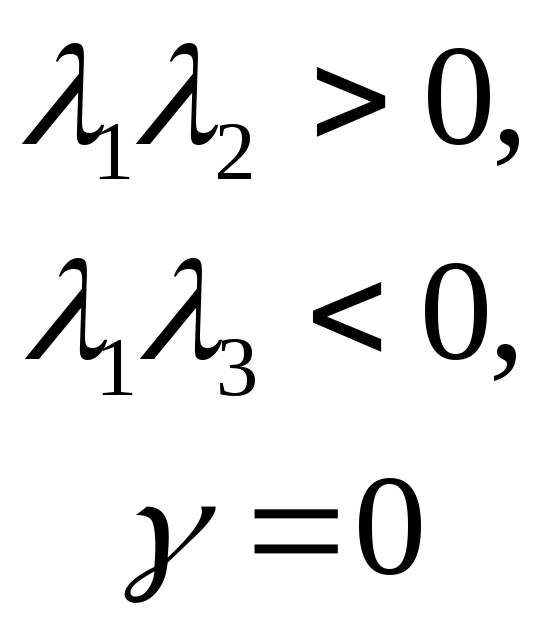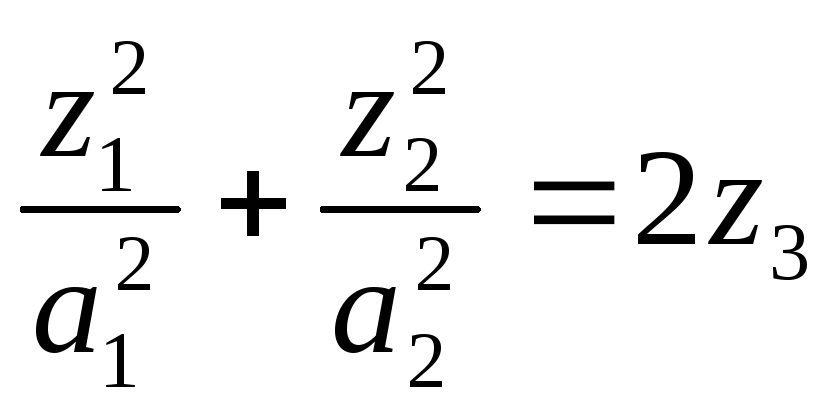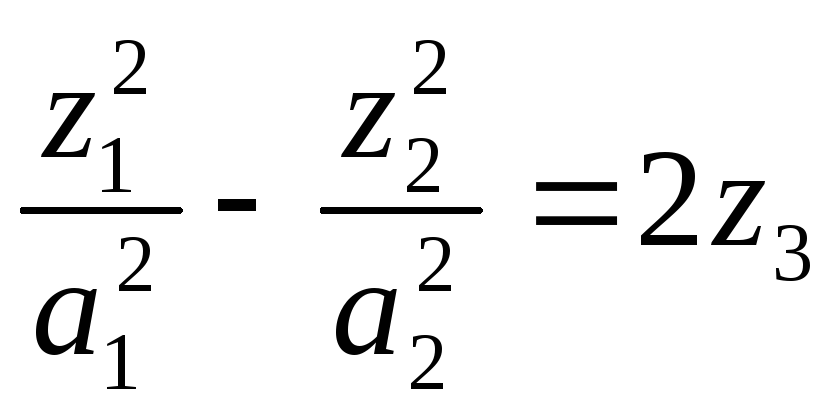- •Примеры:
- •Лемма. Образ и ядро линейного оператора φ являются соответственно подпространствами w и V.
- •Вычисление собственных векторов через главные миноры
- •Билинейные функции.
- •Афинное система координат.
- •Линии и поверхности.
- •Аффинная класификация кривых и поврехностей 2-го порядка.
- •Линейные преобразования унитарного простарнства.
- •Комплексификация евклидова пространства.
- •Ортогональная классификация кривых и поверхностей 2-го порядка.
Ортогональная классификация кривых и поверхностей 2-го порядка.
(1) x![]() Ax+2a
Ax+2a![]() x+α=0
–уравнение квадрики.
x+α=0
–уравнение квадрики.
(2) x=Qy+c
detQ![]() 0
0
О. Преобразование (2) наз. изометрией, если матрица Q ортогональная.
(3)
F(y)=y![]() By+2b
By+2b![]() y+β=0
y+β=0
Теорема 1. Если уравнение 3 получено изометрией из уравнения 1, то:
-
Матрица B подобна матрице А и det
 =det
=det .
.
Д-во: B=QTAQ, QT=Q-1 => B = Q-1AQ
![]() =>
=>
![]() ,
т.к. det
,
т.к. det![]() = 1
= 1
2) Если
преобразование не содрежит сдвига
(с=0), то матрица
![]() подобна матрице
подобна матрице
![]()
Д-во: очевидно,
поскольку в данном случае
![]() будет ортогональной матрицей.
будет ортогональной матрицей.
-
Если Q=E и c
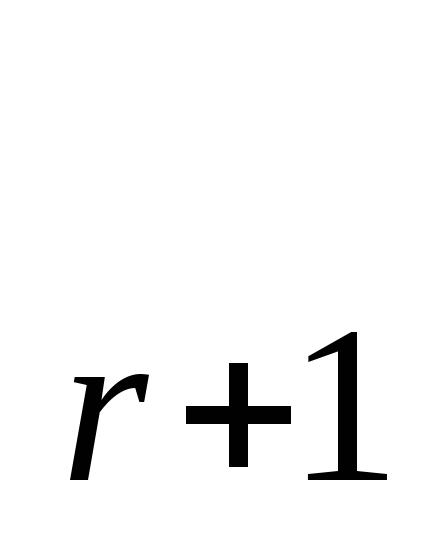 =..=c
=..=c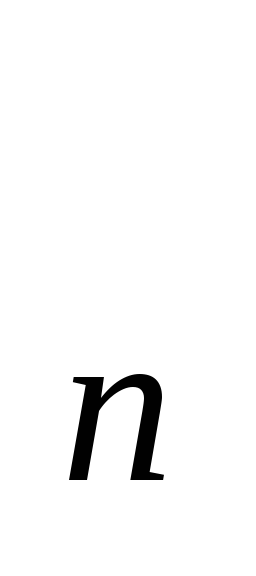 =0,
то Δ
=0,
то Δ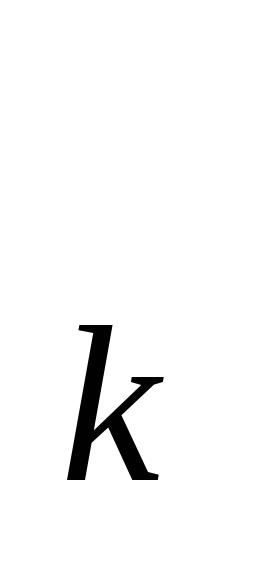 (
( )=Δ
)=Δ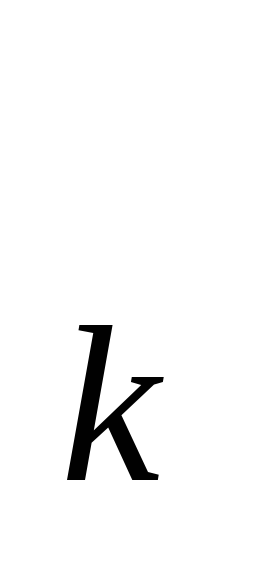 (
( )
(k=r+1,..,n)
)
(k=r+1,..,n)
Д-во: В данном случае
матрица
![]() будет иметь следующий вид:
будет иметь следующий вид:

Рассмотрим произведение
![]()
![]() .
По формуле Бине-Коши получаем, что
минор Δ
.
По формуле Бине-Коши получаем, что
минор Δ![]() (
(![]()
![]() )
равен сумме произведений миноров,
расположенных в первых k
строчках матрицы
)
равен сумме произведений миноров,
расположенных в первых k
строчках матрицы
![]() ,
и миноров, расположенных в первых k
столбцах матрицы
,
и миноров, расположенных в первых k
столбцах матрицы
![]() ;
из последних не равен нулю только угловой
минор, он равен 1. Затем умножим
;
из последних не равен нулю только угловой
минор, он равен 1. Затем умножим
![]()
![]() на
на
![]() и проведем те же рассуждения.
и проведем те же рассуждения.
Следствие. Характеристические многочлены и собственные числа матриц А и В одинаковы, т.к. они подобны.
Собственные числа и сумма главных миноров k-ого порядка матриц А и В – ортогональные инварианты.
Собственные числа и сумма главных миноров k-ого порядка расширенных матриц – ортогональные полуинварианты (с=0).
Теорема 2. Для
любого уравнения (1) существует матрица
Q такая, что преобразование
x=Qy переводит его в (4)
![]() =0,
где λ
=0,
где λ![]() и b
и b![]() определяются единственным образом
с точностью до перестановки.
определяются единственным образом
с точностью до перестановки.
Д-во: выделим квадратичную форму и приведем ее к каноническому виду.
Теорема 3. Если
![]() ≤r+1,
то существует изометрия (2), приводящая
уравнение (1) к (5)
≤r+1,
то существует изометрия (2), приводящая
уравнение (1) к (5)
![]() =0,
где λ
=0,
где λ![]() определяются единственным образом с
точностью до перестановки, а β=
определяются единственным образом с
точностью до перестановки, а β=![]()
Д-во: Применим
теорему 2, тогда матрица
![]() будет иметь вид:
будет иметь вид:
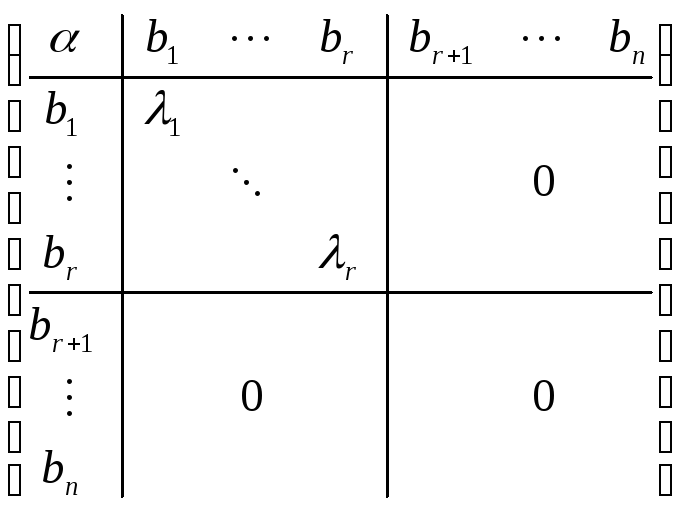
Заметим,
что сдвига мы не осуществляли. Докажем,
что b![]() =..=b
=..=b![]() =0.
=0.
Индексацию в матрице будем вести с 0 и до n. (Матрица n+1 порядка)
Рассмотрим в матрице
![]() все главные миноры r+1 порядка
все главные миноры r+1 порядка
![]() ,
где I: 0≤
,
где I: 0≤![]() ≤n,
J: 0≤
≤n,
J: 0≤![]() ≤n
≤n
Если i![]() >r,
то i
>r,
то i![]() >r,
т.е. две строчки имеют индекс больше r.
Но тогда они пропорциональны, а
следовательно минор равен 0. Т.о. i
>r,
т.е. две строчки имеют индекс больше r.
Но тогда они пропорциональны, а
следовательно минор равен 0. Т.о. i![]() ≤r.
Аналогично для столбцов J.
≤r.
Аналогично для столбцов J.
Возьмем минор r+2 порядка. Если две строчки имеют индексы больше r, то этот минор равен 0.
S![]() - сумма главных миноров r+2
порядка, а из предыдущих рассуждений
следует, что I={0,..,r,k}, J={0,..,r,k},
где r+1≤k≤n. Минор с такими
строчками равен
- сумма главных миноров r+2
порядка, а из предыдущих рассуждений
следует, что I={0,..,r,k}, J={0,..,r,k},
где r+1≤k≤n. Минор с такими
строчками равен
![]() =
=![]()
Т.о.
S![]() (
(![]() )=S
)=S![]() (A)(
(A)(![]() ),
но S
),
но S![]() (
(![]() )=0,
т.к.
)=0,
т.к.
![]() ≤r+1.
А это возможно только когда b
≤r+1.
А это возможно только когда b![]() =..=b
=..=b![]() =0.
=0.
Далее
производим следующее преобразование
![]() j=1,..,r. Выделяем полные квадраты, линейная
часть зануляется.
j=1,..,r. Выделяем полные квадраты, линейная
часть зануляется.
Тогда матрица
![]() перейдет в матрицу
перейдет в матрицу
![]() ,
которая имеет вид
,
которая имеет вид
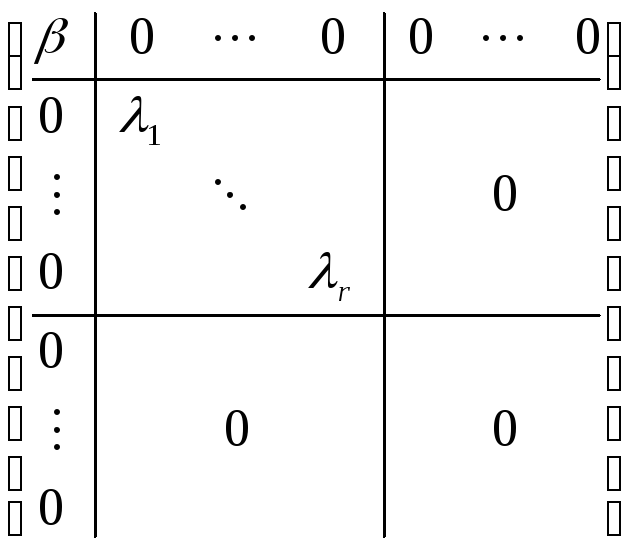
Мы осуществляем сдвиг для первых r компонент, поэтому по пункту 3 из теоремы 1
S![]() (
(![]() )=Δ
)=Δ![]() (
(![]() )=
Δ
)=
Δ![]() (
(![]() )=βS
)=βS![]() (A)
=> β=
(A)
=> β=![]() ,
т.к. S
,
т.к. S![]() (
(![]() )=S
)=S![]() (
(![]() ),
т.к. сначала сдвига не делали.
),
т.к. сначала сдвига не делали.
Теорема 4. Если
![]() =r+2,
то существует изометрия (2), приводящая
уравнение (1) к (6)
=r+2,
то существует изометрия (2), приводящая
уравнение (1) к (6)
![]() =0,
где λ
=0,
где λ![]() определяются единственным образом с
точностью до перестановки, а μ²=-
определяются единственным образом с
точностью до перестановки, а μ²=-![]()
Д-во: Применим теорему
2. Получим матрицу
![]() ,
которая имеет вид
,
которая имеет вид
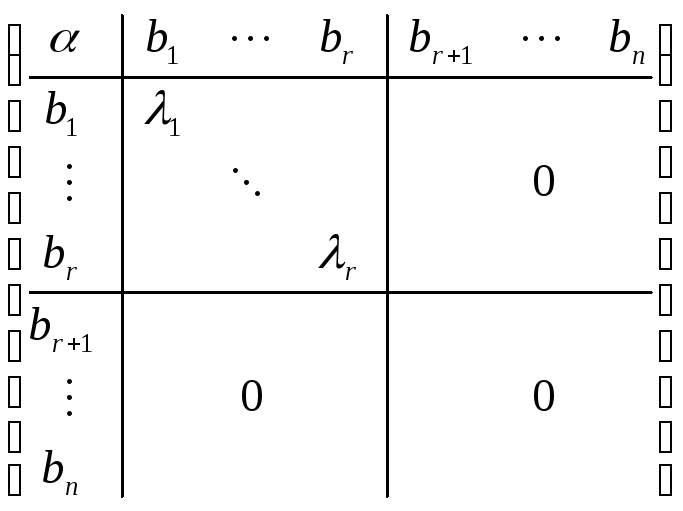
Далее делаем
преобразование
![]() j=1,..,r. Матрица
j=1,..,r. Матрица
![]() примет вид
примет вид
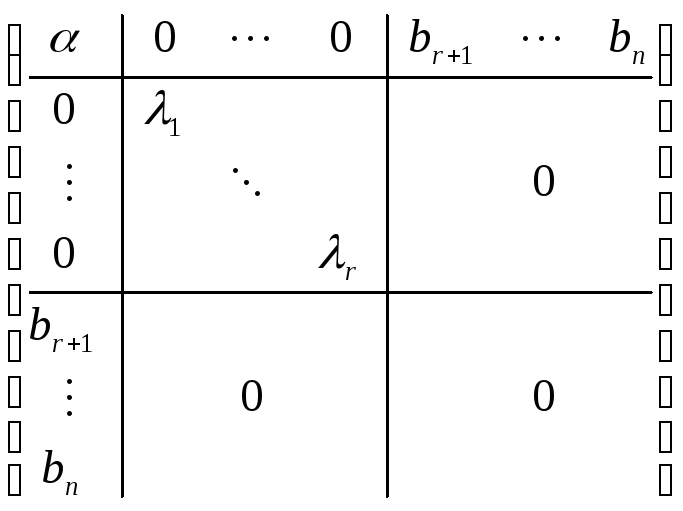
А уравнение
примет вид (4’)
![]() =0
=0
Из теоремы
3 следует, что S![]() (
(![]() )=S
)=S![]() (A)(
(A)(![]() )
)
Обозначим
μ²=![]() =-
=-![]() >0,
т.к. среди коэффициентов b
>0,
т.к. среди коэффициентов b![]() есть ненулевой.
есть ненулевой.
Найдем ортогональное
преобразование, заменяющее линейную
часть одним слагаемым μz![]() .
Для этого в (n-r)-мерном
пространстве строк рассмотрим
вектор-строку 1/μ(b
.
Для этого в (n-r)-мерном
пространстве строк рассмотрим
вектор-строку 1/μ(b![]() ,…,b
,…,b![]() )=b’.
|b’|=1 => любую
ортонормированную систему можно
дополнить до ортонормированного базиса
b’,b²,..,b
)=b’.
|b’|=1 => любую
ортонормированную систему можно
дополнить до ортонормированного базиса
b’,b²,..,b![]() .
Сделаем ортогональную замену переменных
Q
.
Сделаем ортогональную замену переменных
Q![]() z=z’,
где
z=z’,
где
Q![]() =
=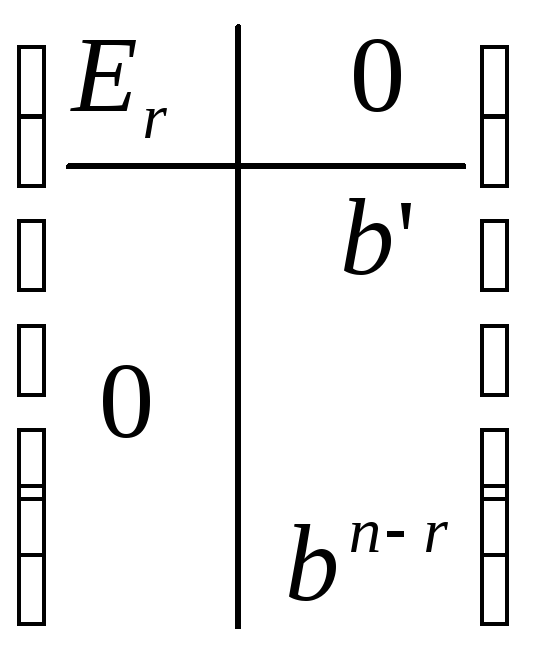 Очевидно, что матрица Q
Очевидно, что матрица Q![]() - ортогональная.
- ортогональная.
![]()
уравнение (4’)
примет вид
![]() =0
=0
![]() =
=![]() Мы получим (6).
Мы получим (6).
Дальнейшее упрощение уравнения можно получить умножением на ненулевоу число (вообще говоря не существое такой изометрии, равносильной такому преобразованию).
Из уравнения (5) получается
(5’)
![]() =1,
если β≠0 или
=1,
если β≠0 или
(5”)
![]() =0
при β=0
=0
при β=0
Из уравнения (6) можно получить
(6’)
![]() положив
положив
![]() >0
>0
Теорема. Для любого уравнения квадрики существует декартова система координат, в котором уравнение квадрики записывается в одном из этих типов и разные уравнения нельзя получать одно из другого изометрией и домножением на ненулевое число.
Д-во: следует из всех выше изложенных рассуждений
Теорема. Для любой кривой второго порядка существует прямоугольная декартова система координат, в которой уравнение кривой имеет один из следующих типов или видов: (нельзя с помощью изометрии перейти от одного уравнения к другому)
|
Название кривой |
Каноническое уравнение |
Условия для коэффициентов |
|
Эллипс |
|
|
|
Мнимый эллипс |
|
|
|
Пара мнимых пересекающихся прямых |
|
|
|
Гипербола |
|
|
|
Пара пересекающихся прямых |
|
|
|
Пара параллельных прямых |
|
|
|
Пара мнимых параллельных прямых |
|
|
|
Пара совпадающих прямых |
|
|
|
Парабола |
|
|
Tеорема. Для любой поверхности 2-го порядка существует прямоугольная декартова система координат, в которой уравнение поверхности имеет один из следующих типов или видов.
Сначала, рассмотрим
канонические уравнения поверхностей
2 порядка, не содержащие переменной
![]() .
Все они представлены в предыдущей
таблице, а канонические уравнения восьми
остальных поверхностей − в следующей
таблице.
.
Все они представлены в предыдущей
таблице, а канонические уравнения восьми
остальных поверхностей − в следующей
таблице.
|
Название поверхности |
Каноническое уравнение |
Условия для коэффициентов |
|
Эллипсоид |
|
|
|
Мнимый эллипсоид |
|
|
|
Мнимый конус |
|
|
|
Однополостный гиперболоид |
|
|
|
Двуполостный гиперболоид |
|
|
|
Конус |
|
|
|
Эллиптический параболоид |
|
|
|
Гиперболический параболоид |
|
|
Приведение пары квадратичных форм к каноническому виду.
Теорема.
Пусть квадратичной форме f(x,x)
соответствует матрица A,
а g(x,x)
– B,
причем В
– положительноопределенная, тогда
существует базис
![]() ,
в котором
,
в котором
![]()
Д-во: A, B – симметричные. B – положительно определенная, тогда ее по теореме Лагранжа можно привести к нормальному виду и для матрицы B этот вид будет E.
![]() -
симметричная. Далее делаем приведение
полученной матрицы A
-
симметричная. Далее делаем приведение
полученной матрицы A![]() к главным
осям: существует ортогональная матрица
к главным
осям: существует ортогональная матрица
![]() ,
что
,
что
![]() .
Из ортогональности
.
Из ортогональности
![]() следует, что
следует, что
![]() .
.
Итак,
мы нашли Q=![]() Q
Q![]() такую, что
такую, что
![]()
Следствие. Характеристический многочлен Пучка det(A-λB); его корни есть диагональные элементы D
Д-во:
![]() ;
det(
;
det(![]() )=det(D-λE)=
)=det(D-λE)=
![]()
С другой стороны
det(![]() )=
)=![]() => корни одинаковые, т.к. многочлены
получились одинаковые.
=> корни одинаковые, т.к. многочлены
получились одинаковые.