Геометрия и алгебра

Пусть даны два линейных пространства V и W над одним и тем же полем F.

О. Отображение φ линейного пространства V на линейное пространство W наз. линейным оператором, если x, x’V и αF:

φ(x+x’)=φ(x)+φ(x’)

φ(αx)=αφ(x)

О. Если W=V, то оператор наз. линейным преобразованием пространства V.

Из свойств линейного оператора с помощью математической индукции можно доказать, что φ()=

Примеры:

1. Пусть дана прямая сумма V=VV, т.е. для xV существует единственное представление x=x+x, где xV, xV.

x= - оператор проектирования на подпространство V параллельно подпространству V.

2. Нулевой оператор -xV φ(x)=0

3. Тождественное преобразование

О. Образом (множеством значений) линейного оператора φ наз. множество векторов из W, для которых в V существует хотя бы один прообраз. Таким образом

Imφ=φV={y/xV, φx=y}

О. Ядром (нуль-пространтсвом) линейного оператора φ наз. множество векторов пространства V, образами которых являются нулевые векторы, т.е.

Kerφ={xV/ φx=0}

Лемма. Образ и ядро линейного оператора φ являются соответственно подпространствами w и V.

Д-во: 1) Очевидно, что φV не пустое. Тогда для y,yφV найдутся такие x,xV, что φx=y, φx=y. Тогда y+y=φ(x+x)φV. Аналогично αyφV

2) φ0=0, поэтому Kerφ не пустое. пусть x,x Kerφ. Тогда φ(x+x)=φx+φx=0. Т.о. x+x Kerφ, аналогично αxKerφ.

О. Размерность образа линейного оператора φ наз. рангом этого оператора и обозначается rankφ. Размерность ядра линейного оператора φ наз. дефектом этого оператора и обозначается defφ.

Пример. Рассмотрим оператор дифференцирования для V=W=F[x].

F[x]= F[x]

Ker=F[x]

Матрица линейного оператора

V=F, W=F

Пусть базис линейного пространства V, тогда любой вектор x этого пространства можно разложить по этому базису. Но тогда получаем, что:

x= dimV=n, т.е. [x]=

φx=φ()=

Таким образом, для задания линейного оператора достаточно задать φ на базис V.

Пусть и - базисы соответственно пространств V и W. Поскольку

φW, то его можно разложить по базису . Пусть φ= (j=1,..,n).

О. Матрица [φ]=Q=(q)F наз. матрице линейного оператора φ в базисах и .

Множество всех отображений V на W обозначается Ф(V,W).

Теорема. Задание базисов в V и в W определяет биективное отображение Ф(V,W) на F. При этом справедлива формула [φ][x]=[φx].

Д-во:

1)Для каждой матрицы Q из F найти линейный оператор из Ф такой, что его матрица [φ]=Q

В качестве φ возьмем . x=.

Тогда если зададим φx=, то оператор φ будет линейным. Это легко доказывается.

Докажем однозначность определения матрицы Q. Пусть AB, т.е. существуют такие i и j, что ab. Из этого и из того, что φe= и ψe=, следует, что φeψe. φ,ψФ(V,W)

2) y=φx= В силу единственности разложения по базису имеем, что (i=1,..,n) => [y]=A[x].

Т.о. любой линейный оператор сводится к умножению матрицы на столбце, если задать базисы.

Действия с линейными операторами.

Суммой двух операторов φ,ψФ(V,W) такое преобразование χ, что для любого x из V χ(x)=φx+ψx. χ=φ+ψ.

Произведением оператора φФ(V,W) на число αF наз. такой оператор χ, что для любого x из V χ(x)=αφx. χ=αφ.

Следствие. Ф – линейное пространство изоморфное линейному пространству F.

Легко доказывается выполнение аксиом.

Д-во: Поскольку уже доказано, что отображение Ф→F является биективным, осталосось доказать, что сохраняется сложение и умножение на число, т.е.

[αφ+βψ]=[αφ]+[βψ]. Пусть [φ]=A, [ψ]=B

(αφ+βψ)e=αφ e+βψe=α+β=.

Т.о. Ф~F.

Пусть даны 3 пространства над одним полем и два оператора φ:V→W и ψ:W→U. Тогда произведением операторов наз. ψφx=ψ(φx).

Лемма. Если ψ и φ линейные операторы, то ψφ тоже линейный оператор ψφФ(V,U).

(ψφ)(αx+α’x’)= ψ(φ(αx+α’x’))= ψ(αφx+α’φx’)=αψ(φx)+α’ψ(φx’)=α(ψφ)x+α’(ψφ)x’.

Следствие. Если в пространствах V,W,U заданы базисы , и соответственно, то [ψφ]=[ψ][φ].

Д-во: Рассмотрим вектор x из V, тогда вектор y=φx принадлежит W, причем [y]=[φ][x]. z=ψy=(ψφ)x => [z]=[ψ][y]= [ψ][φ][x]. Но [z]=[ψφ][x].

Так как операторы можно складывать и умножать на число, то получаем, что Ф – кольцо.

Изменение матрицы линейного оператора при изменении базисов.

Теорема. Пусть дан линейный оператор φ: V→W. Пусть даны матрицы перехода Q и S от базисов и соответственно к базисам и . Тогда [φ]= S[φ]Q.

Д-во: [φ]=A, [φ]=A’.

[x]=Q[x] и [y]=S[y]

S[y]=[y]=A[x]=AQ[] => [y]=SAQ[x] S существует, т.к. S невырожденная

Но [y]=A’[x]. Т.о. A’= SAQ.

О. Пусть даны матрицы A и B, принадлежащие F. Тогда В наз. эквивалентной А над полем F, если существуют невырожденные матрицы TF и QF такие, что B=TAQ.

Следствие. Матрицы, соответствующие одному и тому же линейному оператору в различных базисах эквивалентны. BA

Теорема. Ранг матрицы не меняется при умножении на невырожденную матрицу.

Д-во: докажем, что rank(TA)=rankA

T невырожденная => существует T A= T(TA).

Тогда по теореме (Ранг произведения матриц не выше ранга каждого из сомножителей) имеем, что rank(TA)rankA. Но по этой же самой теореме получаем, что rankArank(TA). Из этого и получаем, что rank(TA)=rankA.

Теорема. Матрицы эквивалентны тогда и только тогда, когда их ранги равны.

BA rankB=rankA

Д-во: По предыдущий теореме из эквивалентности легко доказывается равенство рангов.

Докажем, что из равенства рангов следует эквивалентность.

Пусть rankA=r. Тогда элементарными преобразованиями, что эквивалентно умножению на элементарные матрицы, матрицу А можно привести к следующему виду:

TAQ=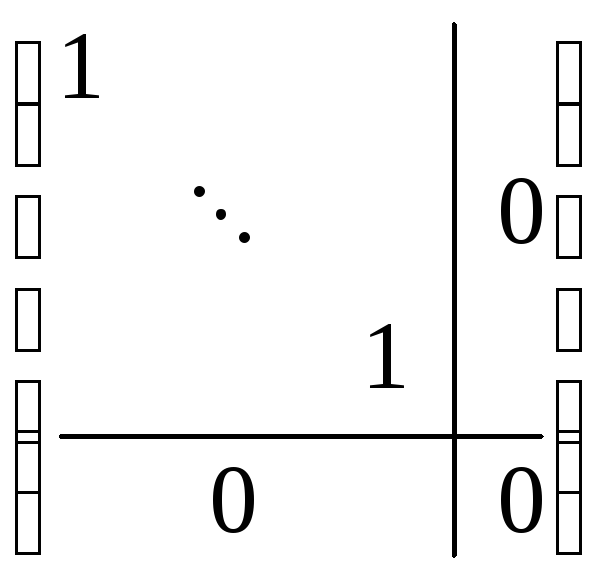 К этому же виду приводится B => TAQ=TBQ =>B= TTAQQ

Матрицы T, Q, T, Q - невырожденные, т.к. они являются произведением элементарных матриц, определитель которых не равен 0.

Следствие 1.

Теорема. rankφ=rank[φ],а defφ+rankφ=dimV

Д-во: Столбцы матрицы [φ] являются координатными столбцами векторов φe. Образ является линейной оболочкой столбцов матрицы. Поэтому dim(Imφ)=rank[φ].

Рассмотрим ядро Kerφ. Оно является множеством решений (а точнее пространством) решений системы [φ]x=0. А как известно размерность пространства решений dim(Kerφ)=dimV-rank[φ].

Рассмотрим теперь линейное преобразование φ пространства V, т.е. φ:V→V.

Ф(V) – множество всех линейных преобразований пространства V на полем F.

Если φФ(V), а базис V, то [φ] - матрица линейного преобразования в этом базисе.

Если φx=y, то [φ][x]=[y].

Если есть еще базис , а Q матрица перехода от старого базиса к новому, то

[φ]= Q[φ]Q

О. Матрица B наз. подобной матрице А над полем F (BA), если существует невырожденная матрица QF (detQ0) такая, что B=QAQ.

Т.о. класс матриц линейного преобразования φ в различных базисах состоит из подобных друг другу матриц.

Теорема. Отношение подобия есть отношение эквивалентности.

Д-во: Рефлективность A=EAE

Симметрия B=QAQ => A=QBQ

Транзитивность С= QBQ= QQAQQ=(QQ)A(QQ)

О. Подпространство W пространства V наз. инвариантным относительно линейного преобразования φ, если любого вектора x из W φx также лежит в W.

Лемма. Ядро и образ линейного преобразования являются инвариантными преобразованиями.

Д-во: Рассмотрим φ(Kerφ). Для любого вектора x из Kerφ φx=0. Но 0Kerφ, поэтому φ(Kerφ)Kerφ.

Рассмотрим φ(Imφ). Так как для любого вектора x из V φx принадлежит образу, то для любого вектора y из Imφ, φy принадлежит образу, а это и означает, что образ инвариантное подпространство.

Теорема. Пересечение и сумма инвариантных относительно φ подпространств инвариантно.

Д-во: Пусть W и W инвариантны относительно φ. Докажем, что W∩W инвариантно относительно φ. Рассмотрим вектор а из W∩W, т.е. он принадлежит как W, так и W. Тогда φа будет принадлежать как W, так и W, т.е. φа принадлежит W∩W, что и требовалось доказать.

Докажем, что W+W инвариантно относительно φ. Рассмотрим любой вектор а из W+W, тогда он либо принадлежит W, либо W. φа будет также принадлежать либо W, либо W. Поэтому φа принадлежит W+W.

О. Сужением преобразования (индуцированное) φ на инвариантное попространство W наз. такое преобразование ψ: W→W, что для любого x из W ψx=φx.

Пример. Для ядра индуцированное преобразование будет нулевым, для образа тождественным.

О.1 Вектор aV наз. собственным вектором преобразования φ, если он не равен нулю и существует такое λF, что φa=λa.

Число λ наз. собственным числом преобразования φ, соответствующее вектору а.

Очевидно, что L(a) – 1-мерное инвариантное подпространство.

О.2 Базисный вектор одномерного инвариантного подпространства наз. собственным вектором преобразования φ.

Лемма. Матрица линейного преобразования φ имеет диагональный вид тогда и только тогда, когда существует базис из собственных векторов.

Д-во: Пусть - базис из собственных векторов, тогда φe=λe. А тогда матрица А будет иметь диагональный вид, причем по диагонали стоят собственные числа.

Пусть теперь матрица А имеет диагональный вид. Умножив ее на e, получим Аe=λe, т.е. e - собственный вектор

Легко доказать, что φa=λa  (φ-λξ)a=0, т.е. aker(φ-λξ)

Пусть существует базис такой, что [φ-λξ][a]=[0], т.е

(1) ([φ]-λE)x=0. Это однородная система из n уравнений с n неизвестными, которая имеет ненулевое решение. Значит det([φ]-λE)=0 (2)

Пусть теперь существует базис такой, что det([φ]-λE)=0. Тогда система (1) имеет ненулевое решение, тогда найдется ненулевой вектор a, что φa=λa.

О. Если существует матрица А, то матрица А-λЕ наз. характеристической для матрицы А, а уравнение det(А-λЕ)=0 наз. характеристическим уравнением для матрицы А.

Лемма. Число λ является собственным числом преобразования φ тогда и только тогда, когда оно является корнем характеристического уравнения.

Доказательство этого факта приведено выше.

Пусть есть φ, берем любой базис => [φ]=A. Составляем характеристическое уравнение det(А-λЕ)=0. Находим корни и реашем систему (1)

Возьмем другой базис и Q матрица перехода. Получаем [φ]=В=QАQ

B-λЕ=QАQ-λЕ=QАQ-λQЕQ=Q(А-λЕ)Q

det(B-λЕ)=det(Q(А-λЕ)Q)=detQdet(А-λЕ)detQ=(detQ)det(А-λЕ)detQ=det(А-λЕ)

Т.о. у подобных матриц характеристические многочлены одинаковы.

det([φ]-λE) – характеристический многочлен φ в любом базисе

Теорема. Линейного преобразование комплексного линейного пространства (линейного пространства над алгебраически замкнутым полем) имеет хотя бы 1 собственный вектор.

Д-во: det([φ]-λE) – многочлен степени n с коэффициентами из поля F. Значит существует хотя бы 1 корень λF. Тогда система (1) имеет ненулевое решение.

Следствие 1. Если W инвариатное подпространство относительно φ, то существует собственный вектор принадлежащий сосбтвенный вектор принадлежащий W.

Д-во: рассмотреть сужение преобразования φ, оно имеет хотя бы один сосбтвенный вектор, который будет принадлежать W

Теорема. У любого линейного преобразования φ вещественного линейного пространства существует либо 1-мерное, либо 2-мерное инвариантное подпространство.

Д-во: Проведем комплексификацию пространства V, т.е. из вещественного пространства V получим комплексное пространство

={x+iy, x,yV}

Можно доказать, что полученное таким образом является линейным пространством.

Из Ф() выделим и назовем вещественными такие, что (x+iy)=φx+iφy. Это линейное преобразование.

Если базис V, то он будет базисом и , т.к. любой вектор из можно разложить по этому базису:

Тогда матрица [] будет вещественной ((e+i0)=φe – не комплексное).

Возможны два случая:

1. у характеристического многочлена существует вещественное решение. Тогда этому решению соответствует одномерное инвариантное подпространство.

2. вещественных решений нет. Тогда найдется хотя бы 1 комплексное решение. Пусть λ=α+iβ. Имеем комплексный собственный вектор z=x+iy

([φ]-λE)[z]=0

Рассмотрим L(x,y), докажем, что это 2-мерное инвариантное подпространство.

[z]=[x]+i[y] необходимо доказать, что φx,φyL(x,y)

(z)=(x+iy)=λz=(α+iβ)(x+iy)=(αx-βy)+i(αy+βx)=φx+iφy (из опред. )

Т.о. φx=αx-βy, φy=αy+βx.

Докажем, что x и y линейно независимы.

Пусть существуют u и v, что ux+vy=0. Тогда φ(ux+vz)=u(αx-βy)+v(αy+βx)=0

Пусть x0, тогда, умножив два пердыдущих равенства на vα-uβ и v соотвественно, получим (u²+v²)βy=0, отсюда β=. Но по предположению у нас вещественных решений.

Следствие. Если W инвариатное подпространсто относительно φ, то W содержит либо 1-мерное, либо 2-мерное инвариантное подпространство.

Д-во: взять сужение преобразования φ.