19

Лекция 14 Электромагнитные колебания в электрической цепи Вопросы

1. Колебательный контур.

2. Переменный ток. Активное и реактивное сопротивление электрической цепи.

1. Колебательный контур

Колебательные и волновые процессы, изучаемые в различных разделах физики, проявляют удивительную общность закономерностей. Колебания груза на пружине и процессы в электрическом колебательном контуре протекают очень похожим образом. Однако они имеют различную физическую природу. Чтобы сформулировать, например, задачу о колебаниях груза на пружине, нужно знать законы Ньютона, задача о колебаниях в электрическом контуре требует знания законов электродинамики. Но математические уравнения, описывающие процессы в этих двух системах, оказываются одинаковыми.

Колебательным контуром называется цепь, состоящая из включенных последовательно катушки индуктивности L, конденсатора емкостью С и резистора сопротивлением R.

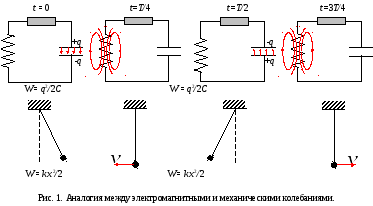
Аналогия между электрическими и механическими величинами

Электрические величины		Механические величины
Заряд конденсатора	q(t)	Координата	x(t)
Ток в цепи		Скорость
Индуктивность	L	Масса	m
Сопротивление	R	Сила трения	Fтр
Магнитный поток	LI	Импульс	mv
Энергия электрического поля конденсатора		Потенциальная энергия пружины
Магнитная энергия катушки		Кинетическая энергия

По закону Ома

; ; ;

при R = 0 . (1)

Решение уравнения свободных гармонических колебаний (1):

, . (2)

, (3)

, (4)

Колебания тока опережают колебания заряда (напряжения) на /2, т.Е. Когда ток достигает максимального значения, заряд обращается в нуль и наоборот.

2. Переменный ток. Активное и реактивное сопротивление электрической цепи

Если на участке цепи происходят изменения силы тока или напряжения, то другие участки цепи могут «почувствовать» эти изменения только через время τ распространения электромагнитного возмущения от одной точки цепи к другой со скоростью света. Время τ много меньше длительности процессов, происходящих в цепи, поэтому считают, что в каждый момент времени сила тока одинакова во всех последовательно соединенных участках цепи. Процессы такого рода в электрических цепях называются квазистационарными.

Квазистационарные процессы можно исследовать с помощью законов постоянного тока, если применять эти законы к мгновенным значениям сил токов и напряжений на участках цепи.

Из-за огромного значения скорости света время установления электрического равновесия в цепи τ оказывается весьма малым. Поэтому к квазистационарным можно отнести многие достаточно быстрые в обычном смысле процессы. Например, быстрые колебания в радиотехнических цепях с частотами порядка миллиона колебаний в секунду и даже выше очень часто еще можно рассматривать как квазистационарные.

2.1. Переменный ток через резистор

,

,

.

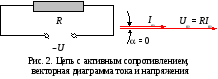
В цепи с активным сопротивлением переменные напряжение и ток совпадают по фазе.

2.2. Переменный ток через катушку с индуктивностью L

; ,

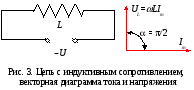
закон Ома:

. (5)

В цепи с индуктивным сопротивлением падение напряжения опережает ток I по фазе на /2.

 реактивное индуктивное сопротивление цепи (6)

При постоянном токе () индуктивное сопротивление отсутствует.

2.3. Переменный ток через конденсатор емкостью С

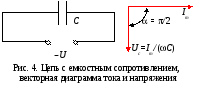
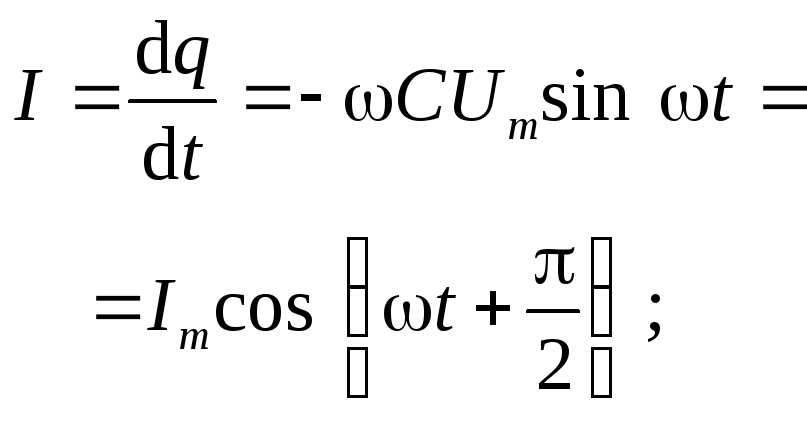
В цепи с емкостным сопротивлением падение напряжения отстает по фазе от тока I на /2.

 реактивное емкостное сопротивление цепи (7)

При постоянном токе () , I_m = 0, постоянный ток через конденсатор не течет.

2.4. Переменный ток в R-L-С цепи

;

;

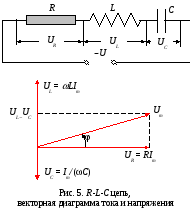
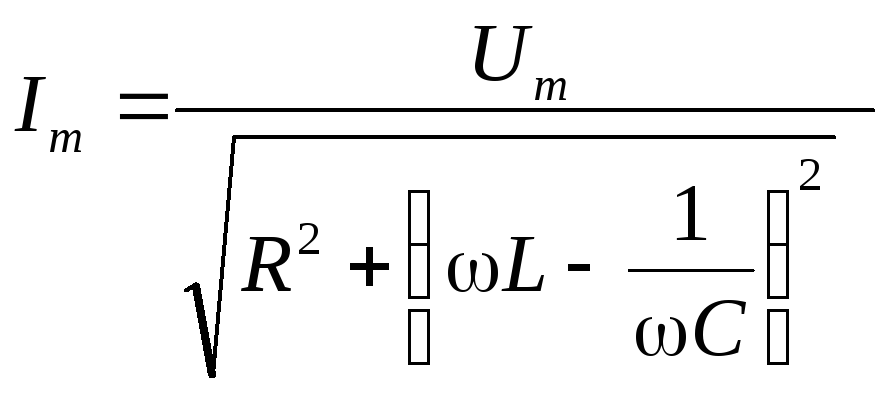(8)

 полное сопротивление цепи;

 реактивное сопротивление цепи;

Глава 2. Электромагнитные колебания и волны

Колебательные и волновые процессы, изучаемые в различных разделах физики, проявляют удивительную общность закономерностей. Колебания груза на пружине и процессы в электрическом колебательном контуре, колебания столба воздуха в органной трубе и ход механических часов, распространение света и звуковых волн и т. д. – все эти явления протекают очень похожим образом. Однако, они имеют различную физическую природу. Чтобы сформулировать, например, задачу о колебаниях груза на пружине, нужно знать законы Ньютона, задача о колебаниях в электрическом контуре требует знания законов электродинамики. Но математические уравнения, описывающие процессы в этих двух системах, оказываются одинаковыми. Аналогично обстоит дело и с волновыми процессами.

Общность колебательных и волновых закономерностей проявляется в общности математических уравнений, описывающих процессы различной физической природы.

Поэтому при изучении электромагнитных колебаний и волн мы будем обращаться за аналогиями к главе «Механические колебания и волны» (часть I, гл. II).