3. Действие магнитного поля на движущийся заряд. Сила Лоренца
Сила Ампера, действующая на отрезок проводника длиной dl с силой тока I, находящемся в магнитном поле B,
![]() (8)
(8)
может быть выражена через силы, действующие на отдельные носители заряда. Элемент тока
![]() (9)
(9)
Подставив (9) в (8) и поделив на число частиц dn, получим силу, действующую на одну заряженную частицу (силу Лоренца)
![]()
![]() (10)
(10)
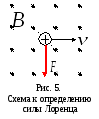
Направление
силы Лоренца, действующей на положительно
заряженную частицу, может быть найдено
по правилу
левой руки.
Если
расположить левую руку так, чтобы линии
![]() индукции магнитного поля входили в
ладонь, а вытянутые пальцы были направлены
вдоль скорости движения частицы, то
отведенный большой палец укажет
направление силы Лоренца.
индукции магнитного поля входили в
ладонь, а вытянутые пальцы были направлены
вдоль скорости движения частицы, то
отведенный большой палец укажет
направление силы Лоренца.
Сила Лоренца всегда направлена перпендикулярно скорости, поэтому при движении заряженной частицы в магнитном поле сила Лоренца работы не совершает.
Частные случаи
-

Рис. 6. Круговое движение заряженной частицы
В однородном
Магнитном поле
Частица движется вдоль линии (
= /2;
sin
= 0; Fл
= 0). Движение
равномерное, прямолинейное.
(
= /2;
sin
= 0; Fл
= 0). Движение
равномерное, прямолинейное. -
Частица движется перпендикулярно линиям
 (
= 0; sin
=1; Fл
= qvB).
Движение равномерное,
по окружности
(
= 0; sin
=1; Fл
= qvB).
Движение равномерное,
по окружности
![]()
![]()
![]()
![]()
 ,
(11)
,
(11)
Рис.
7. Движение заряженной
частицы по спирали

-
Частица движется под углом к линиям
 (
( ).
).
Радиус
спирали:
![]() ,
,
Шаг
спирали:
![]()
Угловая скорость движения заряженной частицы по круговой траектории
![]() (12)
(12)
называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов).
В общем случае, когда на заряженную частицу действуют электрическое и магнитное поля:
![]() .
(13)
.
(13)
Силу, определяемую формулой (13), называют обобщенной силой Лоренца. Учитывая действие двух полей, электрического и магнитного, говорят, что на заряженную частицу действует электромагнитное поле.
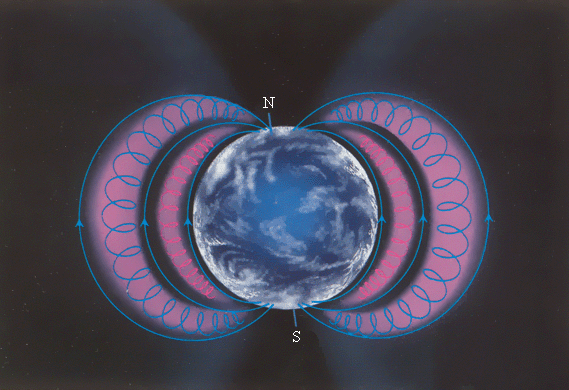
Рис.
8.
Радиационные
пояса Земли