§3. Предикаты и кванторы

n1. Понятие предиката

Желая выделить общее в построении предложений: «3>2», «–5>2», «>2», «>2», и т.д., мы приходим к предложению «х>2», где хR. Предложение «х>2» называют одноместным предикатом или одноместной высказывательной формой. Заметим, что при замене в предложении "х>2" переменной х на конкретное число из R получается конкретное (ложное или истинное) высказывание.

Желая выделить общее в построении предложений:

«Марк Твен – автор повести «Принц и нищий»»,

«Ю. Герман – автор произведения «Царь-рыба»»,

«В. Астафьев – автор романа «Один год»»,

«В. Скотт – автор романа «Айвенго»», и т.д., приходим к предложению «х – автор у», которое называют двуместным предикатом или двуместной высказывательной формой. При замене в предложении «х – автор у» переменной х на конкретное имя писателя, а переменной у на конкретное наименование литературного произведения получим конкретное (истинное или ложное) высказывание.

Дадим «строгое» определение предиката.

Определение 5. Пусть Х₁, Х₂, …, Х_n, где nN, – некоторые непустые множества произвольной природы элементов; х₁, х₂, …, х_n – переменные, множества всех значений которых совпадают с множествами Х₁, Х₂, …,Х_n соответственно; Р(х₁, х₂, …, х_n) – некоторое предложение, содержащее переменные х₁, х₂, …, х_n и превращающееся в конкретное (истинное или ложное) высказывание Р(a₁, a₂, …, a_n) при замене в нем переменных х₁, х₂, …, х_n на конкретные их значения a₁, a₂, …, a_n соответственно, где (a₁, a₂, …, a_n) – произвольный элемент из непустого подмножества D_P декартова произведения Х₁Х₂… Х_n. Тогда предложение Р(х₁, х₂, …, х_n) называется n-местным предикатом или n-местной высказывательной формой с переменными х₁, х₂, …, х_n. Множество D_P называется областью определения предиката Р(х₁, х₂, …, х_n). Если (a₁, a₂, …, a_n)D_P, а истинностное значение высказывания Р(a₁, a₂, …, a_n) равно И (Л), то говорят, что данный предикат является истинным (ложным) в точке (a₁, a₂, …, a_n), иначе при х₁=a₁, х₂=a₂, …, х_n=a_n.

Множество Е_P всех точек из D_P, в которых данный предикат Р(х₁, х₂, …, х_n) является истинным, называется областью истинности предиката Р. В случае, когда Е_P=D_P (Е_P=), данный предикат называется тождественно истинным (тождественно ложным).

Если области истинности двух предикатов Р(х₁, х₂, …, х_n) и Q(х₁, х₂, …, х_n) совпадают, т.е. Е_P=Е_Q, то эти предикаты называются равносильными и пишут: Р(х₁, х₂, …, х_n)Q(х₁, х₂, …, х_n). Если же Е_PЕ_Q, то предикат Q(х₁, х₂, …, х_n) называется следствием предиката Р(х₁, х₂, …, х_n) и пишут: Р(х₁, х₂, …, х_n)Q(х₁, х₂, …, х_n).

Заметим, что иногда одноместные предикаты называют свойствами, а высказывания – 0-местными предикатами.

По существу ранее неявно уже пользовались одноместными предикатами: в записи Aх  Р(х) характеристическое свойство Р(х) элементов множества А является одноместным предикатом, т.е. свойством.

Разницу между понятиями предиката и высказывания можно сравнить с разницей между формуляром анкеты и самой анкетой (формуляр анкеты – заготовленная форма, содержащая определенное число пустых мест, в которые нужно внести некоторые данные, в результате чего и получается то, что называется анкетой).

Пример 1. Любое уравнение или неравенство (система или совокупность) с переменными х₁, х₂, …, х_n, где nN, является n-местным предикатом Р(х₁, х₂, …, х_n). При этом область допустимых значений переменных и множество всех решений данного уравнения или неравенства (системы или совокупности) совпадают с областью определения D_P и областью истинности E_P предиката Р соответственно.

Пример 2. Всякая логическая формула F(Х₁, Х₂, …, Х_n) является частным случаем n-местного предиката, а именно является n-местным предикатом, переменные которого являются высказывательными переменными.

Пример 3. Предикат Р(х)«х²–4х+5>0» с областью определения D_P=R является тождественно истинным (действительно, для каждого числа х₀ из R имеем х₀²–4х+5=(х₀–2)²+1>0, т.е. Р(х₀)=И, поэтому Е_P=R=D_P, т.е. Е_P=D_P).

Пример 4. Предикат Q(х, у)«» с областью определения D_P=R²\(0;0) является тождественно ложным. (Действительно, для каждой пары чисел (х₀; у₀) из D_P имеем , т.е. Q(х₀, у₀)=Л. Поэтому Е_Q=).

Пример 5. Равносильности и следствия для уравнений, неравенств, систем, совокупностей являются соответственно частными случаями равносильностей и следствий для предикатов.

n2. Операции над предикатами

Введем логические операции над предикатами подобно тому, как это было сделано ранее для высказываний, ограничившись лишь одноместными предикатами, определенными на одном и том же множестве.

Определение 6. Пусть Р(х) и Q(х) – некоторые предикаты с переменной х и одной и той же областью определения D. Отрицанием предиката Р(х) называется одноместный предикат с переменной х и областью определения D, обозначаемый одним из символов Р(х) или и являющийся истинным в тех и только в тех точках их D, в которых предикат Р(х) является ложным.

Дизъюнкцией предикатов Р(х) и Q(х) называется одноместный предикат с переменной х и областью определения D, обозначаемый символом Р(х)Q(х) и являющийся ложным в тех и только в тех точках из D, в которых предикаты Р(х) и Q(х) одновременно являются ложными.

Конъюнкцией предикатов Р(х) и Q(х) называется одноместный предикат с переменной х и областью определения D, обозначаемый одним из символов Р(х)Q(х) или Р(х)Q(х) и являющийся истинным в тех и только в тех точках из D, в которых предикаты Р(х) и Q(х) одновременно являются истинными.

Импликацией предикатов Р(х) и Q(х) называется одноместный предикат с переменной х и областью определения D, обозначаемый символом Р(х)Q(х) и являющийся ложным в тех и только в тех точках х из D, в которых одновременно P(х) является истинным, а Q(х) – ложным.

Эквиваленцией предикатов Р(х) и Q(х) называется одноместный предикат с переменной х и областью определения D, обозначаемый символом Р(х)Q(х) и являющийся истинным в тех и только в тех точках х из D, в которых |P(х)| = |Q(х)|.

Дадим геометрическую иллюстрацию введенных выше операций над предикатами.

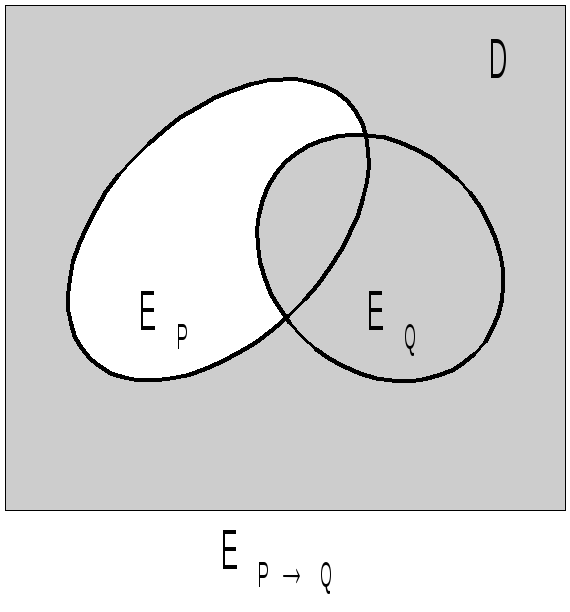
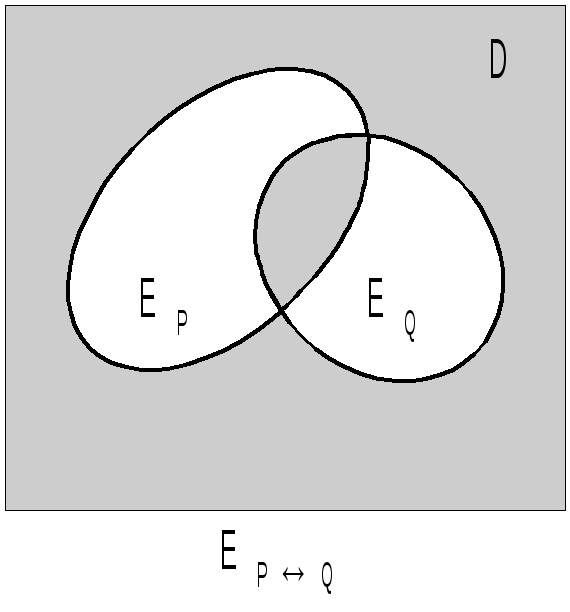
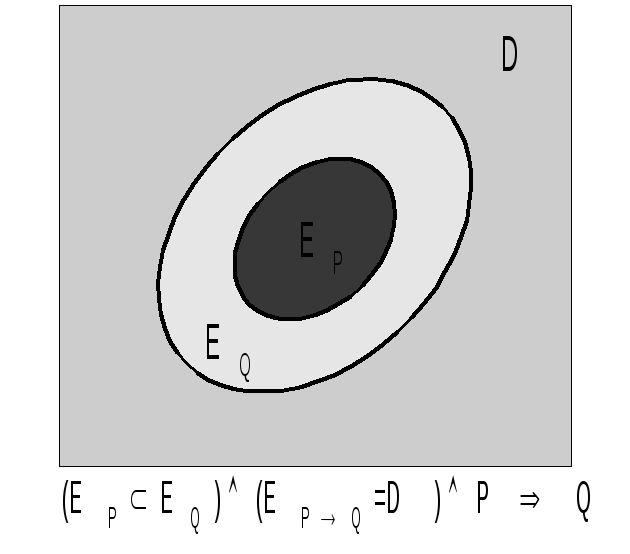
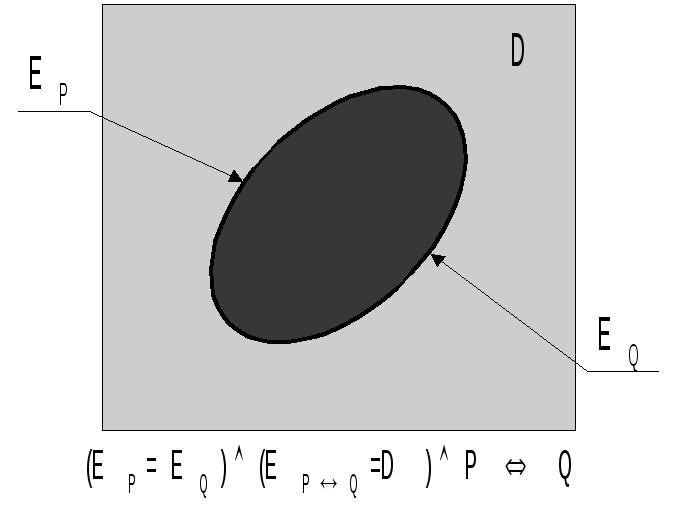
Поясним данную геометрическую иллюстрацию:

1°. Е_Рх | Р(х)=D\E_p.

2°. Е_PQх | Р(x)Q(x)=E_РE_Q.

3°. Е_PQх | Р(x)Q(x)=E_РE_Q.

4°. Е_PQ х | Р(x)Q(x)}=D\(E_Р(D\E_Q))(D\E_P)(D\(D\E_Q)) =(D\Е_Р)E_Q. При переходе (а) воспользовались законом де Моргана для множеств (утверждение 6´ теоремы 1 из n°1 §1 гл.I). При переходе (b) воспользовались очевидным теоретико-множественным равенством С(С_YХ)=Х для случая ХY.

5°. Е_PQ х | Р(х)Q(x) = (E_РЕ_Q)((D\E_P)(D\E_Q))  =(E_PE_Q)(D\(E_PE_Q)). При переходе (с) воспользовались утверждением 6 теоремы 1 из n°1 §1 гл. I.

6°. (Р(х)Q(x)) тогда и только тогда ( по определению 1), когда Е_РЕ_Q, т.е. Е_PQ=D, тогда и только тогда, когда P(х)Q(х) – тождественно истинный предикат.

7°. (Р(х)Q(x)) тогда и только тогда ( по определению 1), когда Е_P=Е_Q, тогда и только тогда, когда предикат Р(х)Q(х) – тождественно истинный, т.е. Е_PQ=D.

Введенные операции для двух предикатов с одной и той же переменной с общей областью определения обобщается на случай двух предикатов с одними и теме же несколькими переменными. Операции нахождения дизъюнкции и конъюнкции для двух предикатов с одним и тем же (несколькими) переменными обобщается на случай любого конечного числа предикатов.

Заметим, что систему уравнений и неравенств с одними и теми же переменными можно рассматривать, как конъюнкцию уравнений и неравенств данной системы; совокупность уравнений и неравенств с одними и теми же переменными можно рассматривать, как дизъюнкцию уравнений и неравенств совокупности.

Пример 6. Систему можно рассматривать, как конъюнкцию (х²+у²+z²–2ху=3)(х+у+z=1)(х–2уz) предикатов Р(х, у, z)=«х²+у²+z²–2ху=3», Q(х, у, z)=«х+у+z=1» и R(х, у, z)=«х–2уz» с одними и теми же переменными х, у, z. Множество всех решений данной системы совпадает с областью истинности этой конъюнкции, т.е. с множеством Е_PЕ_QЕ_R.

Пример 7. Совокупность 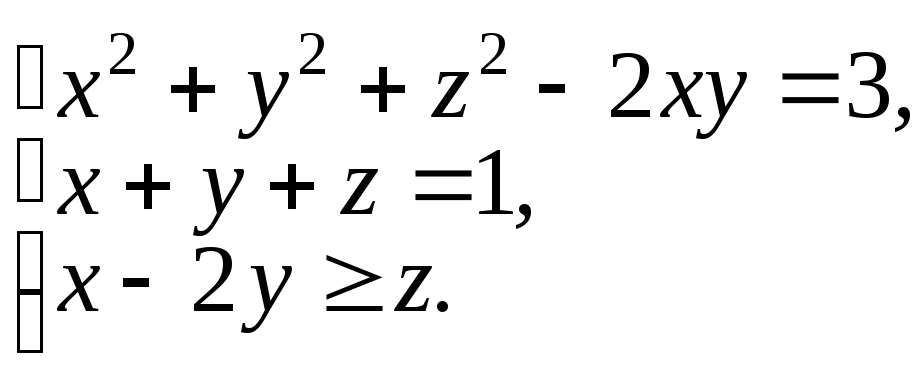, можно рассматривать, как дизъюнкцию P(х, у, z)Q(х, у, z)R(х, у, z) предикатов из примера 6. Множество всех решений данной совокупности совпадает с областью истинности этой дизъюнкции, т.е. с множеством Е_PЕ_QЕ_R..

n3. Операции навешивания кванторов на одноместный предикат

Пусть Р(х) – одноместный предикат с областью определения D_Р. Договоримся символом x (Р(х)) (1) обозначать высказывание: «Для любого значения переменной х из D_Р предикат Р(х) является истинным» (чтение: «Для любого x P от x»). Символ х называется квантором всеобщности по переменной х ( – перевернутая первая буква английского слова «All» и немецкого «Alle» – все). Переход от одноместного предиката Р(х) и к высказыванию (1) носит название операции навешивания на предикат Р(х) квантора всеобщности по переменой х.

Договоримся символом х (Р(х)) (2) обозначать высказывание: «Существует значение переменной х из D_Р, при котором предикат Р(х) является истинным» (чтение: «Существует x такое, что P от x»). Символ х называется квантором существования по переменной х ( – перевернутая первая буква английского слова «exist» и немецкого «existiren» – существовать). Переход от одноместного предиката Р(х) к высказыванию (2) носит название операции навешивания на предикат Р(х) квантора существования по переменной х.

Договоримся символом !х (Р(х)) (3) обозначать высказывание: «Существует единственное значение переменной х из D_Р, при котором предикат Р(х) является истинным» (чтение: «Существует и единственно x такое, что P от x»). Символ !х называют квантором существования и единственности по переменной х. Переход от одноместного предиката Р(х) к высказыванию (3) носит названия операции навешивания на предикат Р(х) квантора существования и единственности по переменной х. Термин «квантор» происходит от латинского слова «quantum» – сколько, как много.

Для частного случая, когда область определения D_Р – конечное множество, а именно, D_Р=а₁, а₂, …,а_n,

имеем:

х (Р(х))Р(а₁)Р(а₂)…Р(а_n) и

х (Р(х)) Р(а₁) Р(а₂)…Р(а_n).

Таким образом, операция навешивания квантора всеобщности (существования) на одноместный предикат Р(х) по переменной х является обобщением операции нахождения конъюнкции (дизъюнкции) конечного числа высказываний.

Полезно следующее утверждение:

Лемма 1. Пусть Р(х) – одноместный предикат. Тогда имеют место следующие равносильности высказываний:

(х (Р(х))хРх; (4)

(х (Р(х))хРх. (5)

Доказательство.

Докажем равносильность (4), т.е. докажем, что(х (Р(х))=х Рх.

1-й этап. Предположим, что (х (Р(х))=И. Тогда по определению отрицания высказывания х(Р(х)) – ложное высказывание. Следовательно, существует такое значение переменной х (например, х=а), для которого предикат Р(х) является ложным, а предикат Р(х) – истинным. Итак, существует такое значение х, при котором Р(х) – истинно, т.е. х (Р(х))=И.

2-ой этап. Предположим, что (х (Р(х))=Л. Тогда по определению отрицания высказывание х (Р(х)) – истинное высказывание. Следовательно, для каждого значения переменной х из D_Р предикат Р(х) является истинным, а предикат Р(х) – ложным. Итак, х ((Р(х))=Л.

Равносильность (4) доказана, равносильность (5) доказать аналогично. Лемма доказана. ■

При построении отрицаний для высказываний, «начинающихся» знаком квантора помимо равносильности (4) и (5) часто бывают полезны следующие равносильности логических формул: , , , которые были установлены в n°2 предыдущего параграфа.

В дальнейшем иногда высказывания вида х (хМР(х)), х ((хх₀)Р(х)), !х ((хх₀)Р(х)), и т.д. будем записывать условно соответственно в виде хМ (Р(х)), хх₀ (Р(х)), !хх₀ (Р(х)), Символы хМ, хх₀, !хх₀ и т.д. называются ограниченными кванторами.

Пример 8. х (х²–5х+6=0 – некоторое высказывание А, получаемое навешиванием на предикат Р(х)=«х²–5х+6=0» квантора всеобщности по переменной х. |A|=Л. Действительно, D_Р =R, 1D_Р, однако 1²–51+6=0 – ложное высказывание, т.е. при х=1 предикат не является истинным.

По лемме 1 имеем:

А=х (х²-5х+6=0)  х ((х²-5х+6=0))  х (х²-5х+60), А=Л.

Пример 9. х2 (х²–5х+6=0) – условная запись высказывания В=х ((х2)  х²–5х+6=0), полученного из предиката Q(х)=«(х2)   х²–5х+6=0» навешиванием квантора существования по переменной х. Данное высказывание истинно. Действительно, D_Q=R и при х=3 предикат Q(х) является истинным: 32  х²–53+6=0 – истинное высказывание. Используя лемму 1 и равносильность , имеем:

 х2 (х²–5х+6=0)х ((х2)(х²–5х+6=0)  х (((х2)  (х²–5х+6=0))  х ((х2)(х²–5х+6=0)  х (х2х²–5х+60),  Л.

n4. Навешивание кванторов на предикаты, имеющие более одной переменной

По аналогии с предыдущем пунктом естественным образом вводятся операции навешивания кванторов на предикат Р(х₁, х₂, …, х_n), где n1, по одной из его переменных х_i, где 1in.

В результате навешивания на предикат Р(х₁, х₂, …, х_n) кванторов всеобщности, существования, существования и единственности по переменной х_i переходим соответственно к (n–1) местному предикату

Q₁(x₁, x₂, …, x_i-1, x_i+1, …, x_n)=x_i(P(x₁, х₂, …, х_n)),

Q₂(x₁, x₂, …, x_i-1, x_i+1, …, x_n)=x_i(P(x₁, х₂…, х_n)),

Q₃(x₁, x₂, …, x_i-1, x_i+1, …, x_n)=!x_i(P(x₁, х₂…, х_n)).

Заметим, что предикаты Q₁,Q₂, и Q₃ имеют (n–1) переменную x₁, …, x_i-1, x_i+1, …, x_n.. Символ х_i хотя и входит в запись этих предикатов, но не является переменной в обычном смысле слова: при замене в этих предикатах символа х_i на конкретное значение получаем предложение, не являющееся предикатом. Чтобы подчеркнуть указанный факт, переменные x₁, ..., x_i-1, x_i+1, …, x_n называют свободными переменными, а переменную х_i – связанной для предикатов Q₁,Q₂,Q₃; говорят еще, что кванторы x_i,x_i, ,!x_i связывают переменную х_i.

Можно привести другие примеры появления связанных переменных:

1. – ложное высказывание, где х – связанная переменная. (При замене в этом предложении переменной х на конкретное значение «теряется» смысл, например, приходим к предложению ).

2 – одноместный предикат с переменной х (n – связанная переменная).

Можно убедится, что для n-местного предиката P(х₁, х₂, … , х_n) имеют место равносильности, аналогичные равносильностям (4) и (5) из формулировки леммы 1.

Пример 10. Q(y) x (x²<y) – одноместный предикат (со свободной переменной y и связанной предикатом существования переменной x), полученный из предиката Р(х, y) = «x²>y» навешиванием квантора существования по переменной x. Этот предикат при y=2 (y = –3) является истинным (ложным).

 Q(y) х(х²у)  х((х²у))х (х²у) – одноместный предикат с переменной у.

Пример 11. R(x, z) y (x+zy²) – двуместный предикат со свободными переменными x, z и связанной переменной у, полученный из предиката U(x, y, z) = «x+zy²» навешиванием квантора всеобщности по переменной у. Этот предикат при х = 1, z=–3 (х =–1, z=3) является ложным, так как высказывание y(1–3 у²) (y(–1+3у²)) является истинным (ложным).

R(x, z) y(x+zy²)  у((x+zy²))  у (x+zy²) – двуместный предикат с переменными x, z.

На (n–1)-местные предикаты Q₁, Q₂ и Q₃ с переменными x₁, …, x_i-1, x_i+1, …, x_n, полученными из n-местного предиката P (x₁, x₂, …, x_n) навешиванием соответственно кванторов всеобщности, существования, существования и единственности по переменной x_i, в свою очередь можно навешивать каждый из трех кванторов по каждой из переменных x₁, …, x_i-1, x_i+1, …, x_n, и т.д.

Так, навешивая на двуместный предикат P(x, y) кванторы всеобщности и существования по каждой из переменных х, у, получаем четыре одноместных предиката:

Q₁(y)x (P(x, y)), Q₂(x)y (P(x, y)), Q₃(y)x (P(x, y)), Q₄(x)y (P(x, y)).

Навешивая в свою очередь на каждый из этих одноместных предикатов кванторы всеобщности и существования, получаем восемь высказываний:

R₁ y (Q₁(y)) y (x (P(x, y))) y x (P(x, y)) (Чтение: «Для любого у и любого х P(x, y)»);

R₂ y (Q₁(y)) y (x (P(x, y)))  y x (P(x, y)) (Чтение: «Существует такое у, что для любого х P(x, y)»);

R₃ x (Q₂(x)) x (y (P(x, y))) x y (P(x, y)) (Чтение: «Для любого х и любого у P(x, y)»);

R₄ x (Q₂(x)) x (y (P(x, y))) x y (P(x, y)) (Чтение: «Существует такое х, что для любого у P(x, y)»);

R₅ у (Q₃(у)) у (х (P(x, y))) у х (P(x, y)) (Чтение: «Для любого у существует такое х, что P(x, y)»);

R₆ у (Q₃(у)) у (х (P(x, y))) у х (P(x, y)) (Чтение: «Существует такое у и существует такое х, что P(x, y)»);

R₇ x (Q₄(x)) x (y (P(x, y))) х у (P(x, y)) (Чтение: «Для любого х существует такое у, что P(x, y)»);

R₈ x (Q₄(x) x (y (P(x, y))) х у (P(x, y)) (Чтение: «Существует такое х и существует такое у, что P(x, y)»).

Пример 12. Конкретизируем сказанное выше. Пусть P(x, y) = «ху» – двуместный предикат с областью определения N² . На базе этого предиката с помощью операций навешивания кванторов всеобщности и существования построим восемь высказываний, найдя истинностностные значения каждого из них.

Если Q₁(y) x (ху), то . Действительно, для любого значения х₀ переменной х из N выполняется неравенство х₀1, а для любого значения у₀ переменной у из N, отличного от 1, (у₀–1)N и ложно высказывание у₀–1у₀. Но тогда высказывание у (Q₁(y)), то есть высказывание у х (ху) ложно, а высказывание у (Q₁(y)), то есть высказывание у х (ху), истинно.

Если Q₂(x) y (ху), то , то есть этот предикат является тождественно ложным. Действительно, предположив существование значения х=х₀, при котором предикат Q₂(x) является истинным, приходим к противоречию: х₀ – наибольшее натуральное число. Но тогда, высказывания х (Q₂(x)) и х (Q₂(x)), то есть высказывания х у (ху) и х у (ху), ложны.

Если Q₃(y) х (ху), то , то есть этот предикат является тождественно истинным. Действительно, для любого значения у₀ переменной у из N существует такое значение х₀ переменной х из N, что х₀у₀ (можно взять например х₀=у₀). Но тогда каждое из высказываний у (Q₃(y)) и у (Q₃(y)), то есть у х (ху) и у х (ху), является истинным.

Если Q₄(x) y (ху), то , то есть этот предикат является тождественно истинным. Действительно, для любого значения х₀ переменной х из N верно, что х₀1. Но тогда высказывания х (Q₄(х)) и х (Q₄(х)), то есть высказывания х у (ху) и х у (ху), являются истинными.

Сравнивая истинностные значения высказываний, построенных в последнем примере, приходим к утверждениям:

х у (P(x, y))  y x (P(x, y)), х у (P(x, y))  y x (P(x, y)), у х (P(x, y)) х у (P(x, y)).

Таким образом, для высказываний, построенных в примере 10, при перестановке «одноименных» кванторов истинностное значение не изменяется, чего нельзя сказать о перестановке «разноименных» кванторов.

Оказывается, что аналогичным свойством обладает любой n-местный предикат при n2, то есть можно доказать утверждение.

Лемма 2. Пусть P(х₁, х₂, … , х_n) – какой-либо n-местный предикат, n2. Тогда имеют место равносильности:

x_i x_j (P(х₁, х₂, … , х_n))  x_j x_i (P(х₁, х₂, … , х_n)),

x_i x_j (P(х₁, х₂, … , х_n))  x_j x_i (P(х₁, х₂, … , х_n)),

где x_i, x_j – какие – либо две различные переменные данного предиката. В то же время равносильностьx_i x_j (P(х₁, х₂, … , х_n))  x_j x_i (P(х₁, х₂, … , х_n)) может и не иметь место.