
- •Томский государственный университет систем управления и радиоэлектроники (тусур) Кафедра промышленной электроники (прэ)
- •Программирование
- •Введение
- •Модель цепи в пространстве состояний.
- •Получение модели цепи в пространстве состояний на основе системы уравнений Кирхгофа.
- •Пример построения модели цепи в пространстве состояний
- •Получение компонентов модели цепи в пространстве состояний на основе матричных операций MathCad
- •Аналитическое решение систем линейных дифференциальных уравнений.
- •Матричная экспонента
- •Некоторые свойства матричной экспоненты
- •Матричная экспонента и преобразование подобия
- •Собственные числа и собственные вектора матрицы
- •Расчет матричной экспоненты на основе преобразования подобия с использованием функций MathCad
- •Решение системы дифференциальных уравнений с использованием матричной экспоненты в MathCad.
- •Собственные числа, колебательный характер переходного процесса и резонансные явления.
- •Рекомендации по выбору значений параметров элементов схемы
- •Расчет реакции схемы на ступенчатое воздействие
- •Реакция цепи на одиночный прямоугольный импульс
- •Реакция цепи на периодическую последовательность прямоугольных импульсов
- •Получение осциллограмм установившегося режима.
- •Трассировка графиков
- •Задание на курсовое проектирование
- •Построение графического изображения схемы
- •Построение системы уравнений Кирхгофа
- •Формирование регионов с определениями основных функций
- •Выбор значений параметров элементов схемы, обеспечивающих колебательный переходный процесс
- •Исследование отклика цепи на включение источника эдс единичной амплитуды.
- •Исследование отклика цепи на прямоугольный импульс
- •Исследование установившегося процесса в цепи при воздействии периодической последовательности импульсов
- •Оформить пояснительную записку в виде файла MathCad с комментариями (см. «Приложение в»).
- •Приложение а
- •Приложение б
- •Приложение в
- •3.1 Операторы определений функций для расчета матричных
- •3.2 Формирование функций расчета матричной экспоненты
- •3.3 Определение функции расчета реакции цепи на включение
- •3.4 Определение функции расчета реакции цепи на одиночный
- •3.5 Определение функций расчета переходного процесса в цепи
- •3.6 Определение функций расчета переходного процесса в цепи
- •3.7 Построение функций, используемых при выборе величин
- •4. Задание численных величин параметров
- •5. Получение реакции цепи на включение единичного источника эдс
- •6. Получение реакции цепи на подключение к источнику эдс,
- •7. Получение реакции цепи на подключение к источнику эдс,
- •8. Получение графиков установившихся процессов при воздействии
Расчет матричной экспоненты на основе преобразования подобия с использованием функций MathCad
В составе встроенных функций векторно-матричной алгебры MathCad имеются функции eigenvals(A) и eigenvecs(A).
Функция eigenvals(A), принимая в качестве аргумента квадратную матрицу A, возвращает набор ее собственных чисел, сформированный в виде вектора.
Функция eigenvecs(A), принимая матрицу A, возвращает матрицу собственных векторов T.
Рассмотрим пример использования этих функций. Зададим квадратную матрицу A в виде матричной константы:

Вызовем функцию расчета собственных чисел этой матрицы и поместим результат в вектор Λ:
![]() , (2.27)
, (2.27)
и выведем значение вектора Λ в численной форме:

Вызовем функцию расчета собственных векторов матрицы A и поместим результат в матрицу T:
![]() ,
(2.28)
,
(2.28)
и выведем значение матрицы T в численной форме:

Таким образом, встроенные функции MathCad Позволяют получить собственные функции и собственные вектора матрицы A.
Функции eigenvals(A) и eigenvecs(A) используют для расчета собственных чисел и собственных векторов численные методы, что неизбежно вызывает, хотя и не большую, ошибку. Оценим уровень ошибок, вычислив матрицу T-1∙A∙T, которая теоретически должна быть диагональной:

Видим, что получившаяся матрица почти диагональная, на ее диагонали, на самом деле, расположены собственные числа матрицы A, Однако, и недиагональные элементы, хотя и малы, но не равны нулю. Это следствие неизбежных ошибок численных методов. Факт возникновения ошибок численных методов обязательно нужно учитывать при возникновении трудно интерпретируемых результатов.
Для вычисления матричной экспоненты eAt на MathCad нам потребуется сформировать диагональную матрицу вида:
 ,
(2.29)
,
(2.29)
причем с учетом физической реализуемости, нужно доопределить экспоненты в диагонали так, чтобы они были равны нулю при отрицательном времени, т.е. DD(Λ, t) должна быть нулевой при t<0.
Сделать это можно, определив функцию пользователя:
EX(a,t) := if(t<0,0,exp(a∙t)) (2.30)
Введенная таким образом функция двух аргументов совпадает с eat только для t ≥ 0, для t<0 она тождественно равна нулю.
В составе палитры матричных операций MathCad имеется оператор векторизации функций (см.п.2.7 в [1]). В нашем случае мы подвергнем векторизации введенную нами функцию EX(a,t) по параметру a.
Функция
![]() –
это векторная функция с элементами:
–
это векторная функция с элементами:
(2.31)
П
(2.32)![]() функцию
diag из состава встроенных
функций MathCad, получим
диагональную матрицу вида:
функцию
diag из состава встроенных
функций MathCad, получим
диагональную матрицу вида:
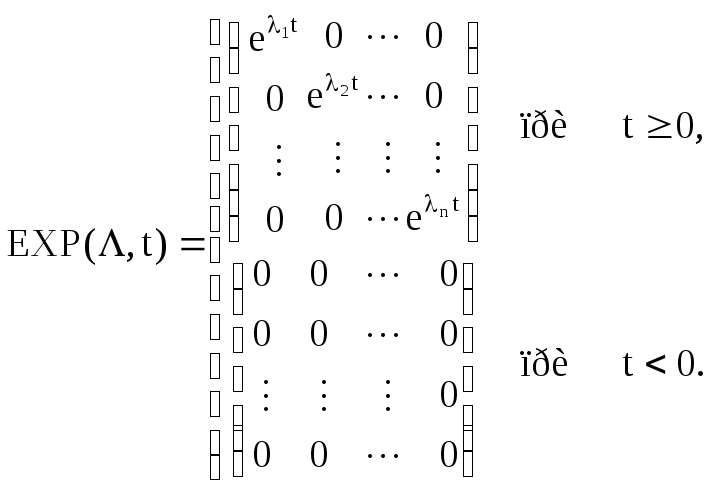
Матрица (2.32) подобна физически реализуемой матричной экспоненте eAt. Остается только воспользоваться обратным преобразованием подобия, чтобы получить выражение для матричной экспоненты в исходной системе координат:
![]() (2.33)
(2.33)
Выражение (2.33) – оператор MathCad, задающий функцию расчета матричной экспоненты (обозначена Ф(Λ,t)) , как функцию вектора собственных значений Λ и времени t.
Итак, порядок расчета матричной экспоненты можно представить в виде следующей последовательности операций:
Определяем собственные числа матрицы A с помощью функции eigenvals(A).
Определяем матрицу собственных векторов матрицы A с помощью функции eigenvecs(A).
Создаем скалярную функцию – «физически реализуемую» экспоненту EX(a,t) := if(t<0,0,exp(a∙t)).
С помощью оператора векторизации
превращаем скалярную функцию EX(a,t)
в векторную функцию и, используя функцию
diag, формируем
диагональную матрицу
![]() .
.
Формируем оператор вычисления матричной
экспоненты,.:
![]()
