Матричная экспонента и преобразование подобия

Рассмотрим систему линейных уравнений, связывающую два n – мерных вектора x и у:

y = A∙x (2.12)

Представим эти уравнения в другой системе координат. Из курса линейной алгебры известно, что переход в иную систему координат аналогичен умножению векторов на матрицу преобразования T. Для взаимнооднозначного преобразования матрица T должна иметь обратную матрицу T^-1. Пусть y1 и x1 – образы векторов y и x в новой системе координат т.е.: y = T∙y1 и x = T∙x1. Из условий однозначности преобразований следует y1 = T^-1∙y и x1 = T^-1∙x. Запишем (2.12) через y1 и x1:

T∙y1= A∙T∙x1 или y1= T^-1∙A∙T∙x1 (2.13)

Система уравнений (2.13) отражает те же связи между векторами, что и система (2.12), только в другой системе координат. Матрицы A и Λ = T^-1∙A∙T в математике называют подобными, а само преобразование матрицы T^-1∙A∙T – преобразованием подобия. Не трудно убедиться, что пара подобных матриц A и Λ связана соотношениями:

Λ = T^-1∙A∙T и A = T∙ Λ ∙T^-1 (2.14)

Преобразование к другой системе координат целесообразно, если в преобразованных координатах система приобретает, в каком-то смысле, более простой вид. Так, например, если удастся найти такое преобразование T, при котором матрица Λ оказывается диагональной, то в преобразованных координатах система (2.13) распадется на n независимых линейных уравнений.

Допустим, что найдено такое преобразование T, которое приводит матрицу A к диагональному виду:

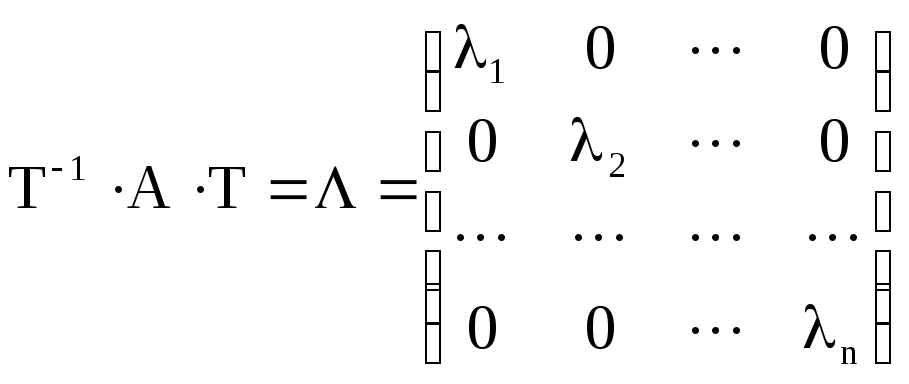. (2.15)

Не трудно убедиться, что это же преобразование приводит к диагональному виду и A^m - любую степень матрицы A:

. (2.16)

Из (2.16) и (2.4) следует, что преобразование T приводит к диагональному виду и матричную экспоненту e^At:

, (2.17) что позволяет получить выражение для e^At в исходных координатах:

. (2.18)

Выражение (2.18) позволяет вычислить матричную экспоненту в случае, если матрицы T и Λ известны. Поиск матриц T и Λ сводится к известной в математике задаче о собственных числах и собственных векторах матрицы.

Собственные числа и собственные вектора матрицы

Собственными числами матрицы A, называют числа λ, в общем случае комплексные, при которых определитель матрицы

(2.19) равен нулю.

Иными словами, собственное число λ матрицы A должно удовлетворять уравнению

. (2.20)

Если раскрыть определитель, то он превратится в полином относительно λ:

, (2.21) где n – размер матрицы A, а коэффициенты p_k зависят только от элементов матрицы A. Уравнение (2.20) примет иметь вид:

, (2.22)

Таким образом, задача о поиске собственных чисел матрицы размера n×n сводится к поиску корней полинома степени n.

В общем случае полином (2.21) может быть представлен в виде произведения:

, (2.23)

где λ_i – различные корни полинома;

m_i – кратность корня λ_i ;

K – число различных корней.

В математике есть т.н. основная теорема алгебры, которая утверждает: всякий полином степени n имеет в поле комплексных чисел ровно n корней, причем каждый корень считается столько раз, какова его кратность. Это означает, что m₁+m₂+…+m_K = n.

Задача поиска корней полинома в аналитическом виде решена лишь для n ≤ 4, для n > 4 возможен только их численный поиск.

С собственным числом матрицы связано понятие собственный вектор. Собственным вектором матрицы A, соответствующим собственному числу λ_i называют вектор t_i, для которого справедливо соотношение:

A∙t_i = λ_i∙t_i , где i = 1…n. (2.24)

Допустим, что матрица A имеет n различных собственных чисел и, соответственно, n собственных векторов. Составим матрицу T, столбцы которой образованы векторами t_i:

и запишем уравнения (2.24) в матричной форме:

(2.25)

Соотношения (2.24) и (2.25) полностью эквивалентны.

Сделаем еще одно предположение: допустим, что собственные вектора линейно независимы. Это допущение справедливо далеко не для всяких матриц, но мы будем считать, что в наших приложениях оно имеет место. Если вектора t_i линейно независимы, то матрица T будет иметь обратную матрицу T^-1. Умножив слева обе части уравнения (2.25) на T^-1 получим:

(2.26)

Таким образом, получаем, что в рамках сделанных нами предположений, матрица A подобна диагональной матрице и преобразование подобия связано с собственными векторами.

На основании вышеизложенного можно предложить один из способов расчета матричной экспоненты e^At по выражению (2.18), используя функции нахождения собственных чисел и собственных векторов из состава встроенных функций математического процессора MathCad.