§4. Задачи математической физики. Метод Даламбера

Для уравнений мат. физики решаются как задача Коши, так и граничные задачи. Различают три вида граничных задач: первого, второго и третьего рода. Пусть решение уравнения (1) §3 ищется внутри или вне некоторой области D c границей Если на границе задано условие

(1)

то это граничная задача первого рода, или задача Дирихле. Если на границе задано условие

(2)

где производная функции по направлению нормали к границе области D, то это вторая граничная задача, или задача Неймана. В третьей, или смешанной задаче, граничные условия записываются в виде:

(3)

Для уравнений Лапласа и Пуассона возможны только граничные задачи. Для уравнений теплопроводности и волнового уравнения решается и задача Коши.

Из основных методов решения уравнений математической физики отметим следующие: метод характеристик, метод интегральных преобразований и метод Фурье (разделение переменных).

Не рассматривая сам метод характеристик, воспользуемся его результатом - решением уравнения колебания струны

(4)

(5)

Непосредственной подстановкой (5) в (4) убедимся, что (5) является решением уравнения (4), если произвольные функции дважды дифференцируемы. Решение называют прямой бегущей волной, а решение обратной бегущей волной. Таким образом, общее решение (5) представляет собой суперпозицию (наложение) прямой и обратной волн.

Струну будем считать бесконечной и решим задачу Коши с начальными условиями (6)

Требуя выполнения начальных условий (6), из (5) получим

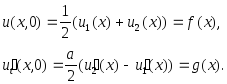
(7)

Интегрируя последнее уравнение из (7), получим

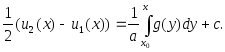(8)

Из (7) и (8) найдем неизвестные функции и

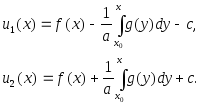(9)

Подставляя (9) в (5), получим решение задачи Коши

(10)

Формула (10) называется решением Даламбера задачи Коши для уравнения колебания струны.

§5. Метод интегральных преобразований

Метод интегральных преобразований является одним из наиболее распространенных методов решения дифференциальных уравнений как обычных, так в частных производных. Ранее (см. §4, гл.2) мы рассмотрели метод преобразования Лапласа решения ОДУ и уравнений в частных производных. Однако, кроме преобразования Лапласа и Фурье (см. §5, гл.3) существуют и другие интегральные преобразования, например, Ханкеля, Меллина, Вебера и др.

Мы воспользуемся синус-преобразованием Фурье

(1)

для решения следующей задачи.

Задача. Полубесконечное тело, ограниченное плоскостью имеет заданное начальное распределение температуры Найти последующее распределение температуры в теле, считая, что с момента времени его граница поддерживается при нулевой температуре.

Решение. Математическая модель этой задачи следующая: найти решение уравнения теплопроводности

(2)

с начальным условием (3)

и граничным условием (4)

Будем считать, что и имеет односторонние производные. Неизвестная функция вместе со своими производными до второго порядка. Тогда, используя преобразование (1), вместо (2-4) получим (2')

(3')

Решение ОДУ с постоянными коэффициентами с начальным условием (3') имеет вид

(5)

Используя обратное синус-преобразование Фурье (1), найдем

(6)

Легко проверить, что (6) удовлетворяет граничному условию (4) и является решением данной задачи. В частности, если то и

(7)