
- •Глава 8. Числовые ряды
- •8.1. Основные понятия
- •8.1. 1. Определение числового ряда
- •8.1.2. Сходимость числового ряда. Сумма ряда
- •8.1.3. Свойства сходящихся рядов
- •8.2. Необходимый признак сходимости числового ряда
- •8.4.2. Признак Даламбера сходимости знакоположительных рядов
- •8.4.3. Радикальный признак Коши сходимости числового ряда
- •8.4.4. Интегральный признак Коши
- •8.5. Знакочередующиеся ряды. Теорема Лейбница
- •8.6. Знакопеременные ряды. Теорема об абсолютной сходимости числового ряда
- •Глава 9. Степенные ряды
- •9.1. Функциональные ряды. Общие понятия
- •9.2. Равномерная сходимость функциональных рядов. Теорема Вейерштрасса
- •9.3. Теорема Абеля о виде области сходимости степенного ряда
- •9.4. Радиус и область сходимости степенного ряда
- •9.5. Ряды Тейлора и Маклорена
- •9.6. Разложение в ряд Маклорена основных элементарных функций
- •9.7. Применение рядов для приближенных вычислений
- •Вопросы к экзамену Неопределённый интеграл
- •Определённый интеграл
- •77. Дифференцирование интегралов, зависящих от параметра. Формула Лейбница. Гамма-функция. Дифференциальные уравнения
- •Шершнев Владимир Григорьевич математический анализ
- •Часть 2. Интегральное исчисление
- •117997, Москва, Стремянный пер. 36.
9.3. Теорема Абеля о виде области сходимости степенного ряда
В общем случае степенной ряд имеет вид
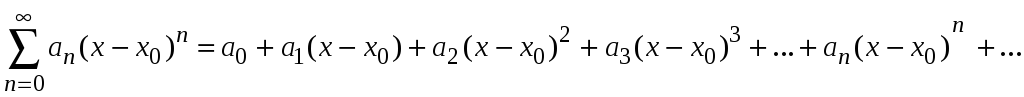 ,
,
где
![]()
постоянные величины, х
– переменная величина.
постоянные величины, х
– переменная величина.
В частном случае
при
![]() ряд имеет вид
ряд имеет вид
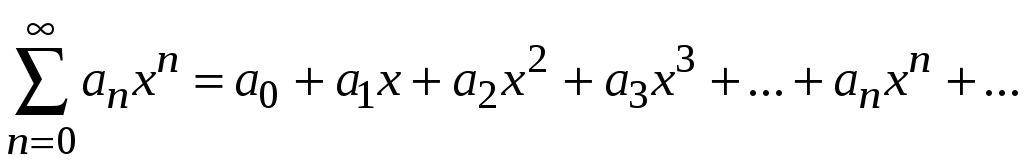 .
.
При конкретных значениях х ряд является числовым и можно исследовать его сходимость и находить область его сходимости.
Теорема 9.2.
(Теорема Абеля).
1. Если степенной ряд
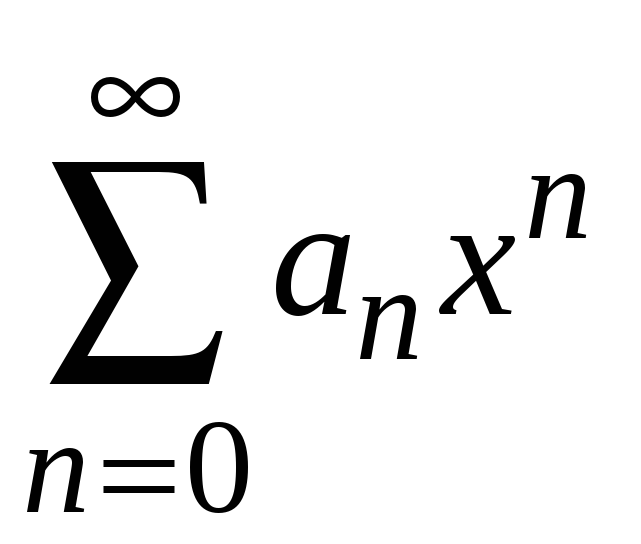 сходится при некотором значении
сходится при некотором значении
![]() ,
то он сходится также при любых значениях
х,
для которых
,
то он сходится также при любых значениях
х,
для которых
![]() .
2. Если степенной ряд расходится при
.
2. Если степенной ряд расходится при
![]() ,
то он также расходится при любых значениях
х,
для которых
,
то он также расходится при любых значениях
х,
для которых
![]() .
.
Д ок а з а т е л ь с
т в о. 1. Пусть степенной ряд
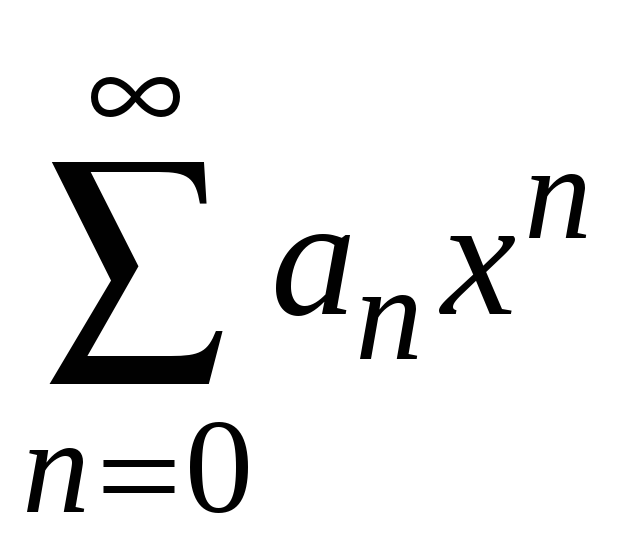 сходится при
сходится при
![]() ,
т. е. ряд
,
т. е. ряд
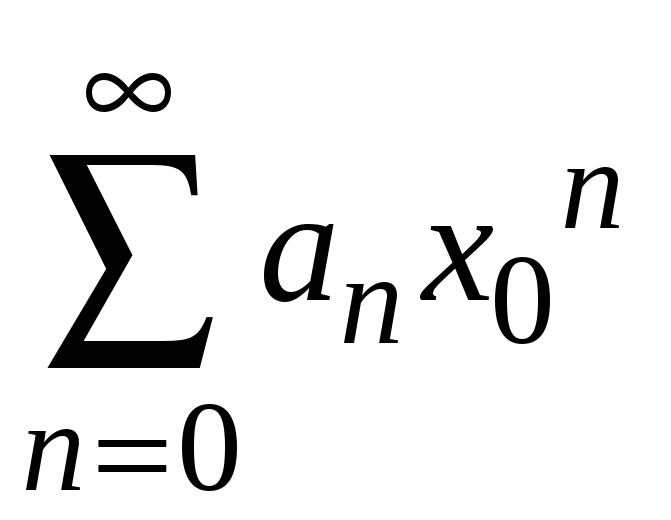 является
сходящимся. Тогда его члены
является
сходящимся. Тогда его члены
![]() ограничены при любых значениях степени
n,
т. е.
ограничены при любых значениях степени
n,
т. е.
![]() ,
где
,
где
![]() .
.
Составим ряд из
абсолютных величин членов исходного
ряда
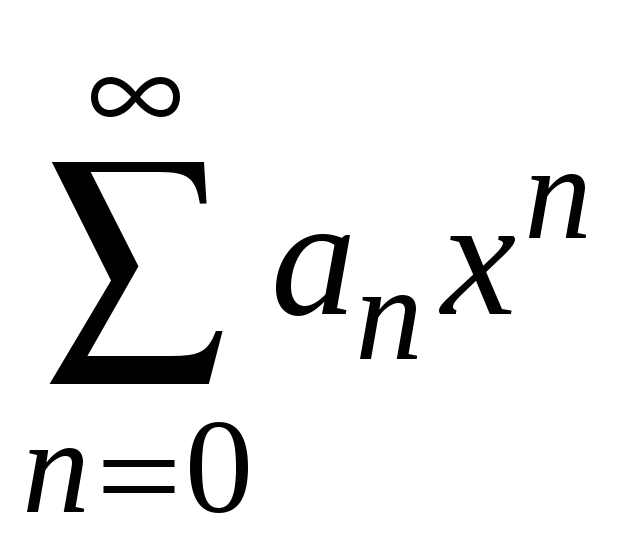
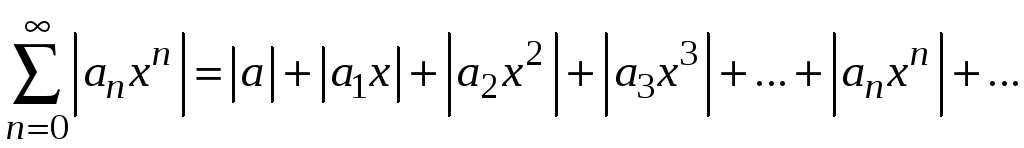 .
.
Покажем, что этот
ряд сходится, если
![]() .
Преобразуем все его члены следующим
образом:
.
Преобразуем все его члены следующим
образом:
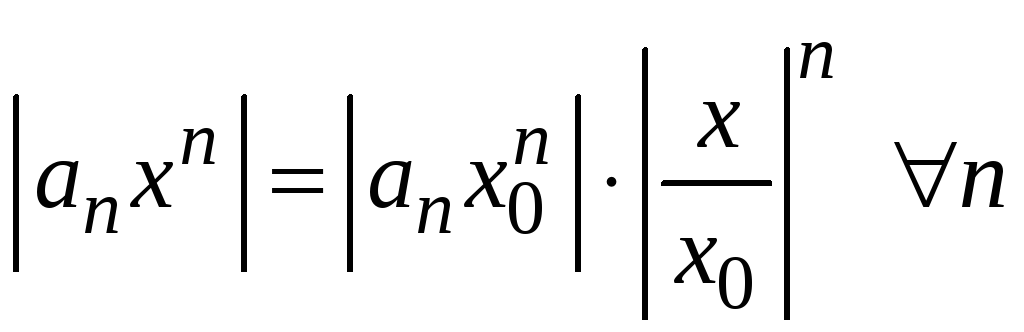 ,
а также учтем, что при
,
а также учтем, что при
![]() все его члены ограничены величиной М.
Тогда можно записать неравенство
все его члены ограничены величиной М.
Тогда можно записать неравенство
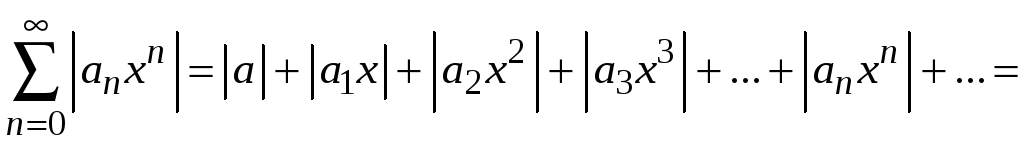
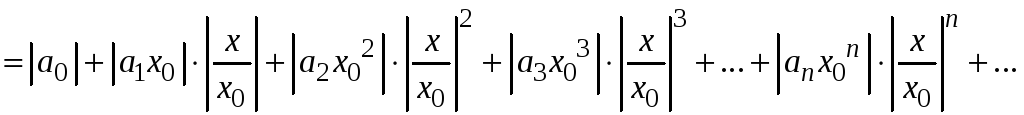
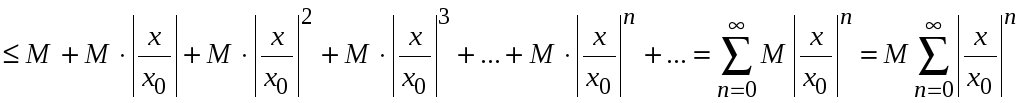 .
.
При
![]() ряд
ряд
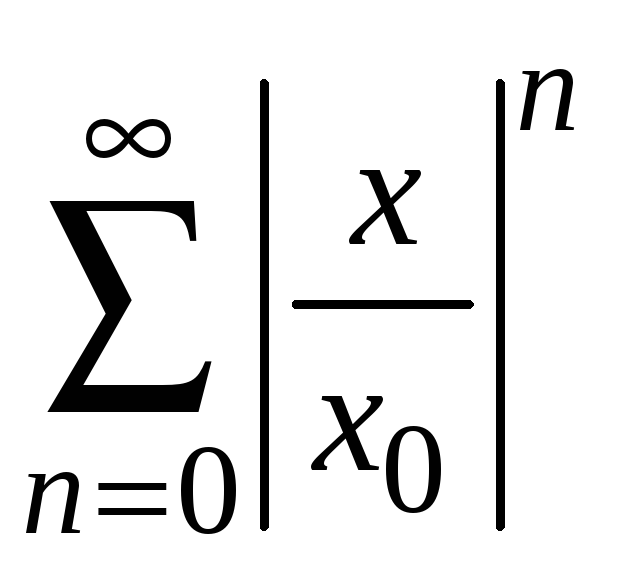 представляет
бесконечную убывающую геометрическую
прогрессию со знаменателем
представляет
бесконечную убывающую геометрическую
прогрессию со знаменателем
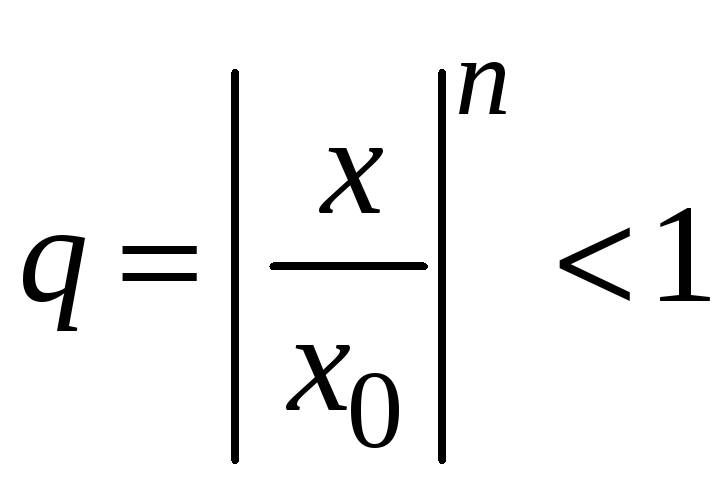 ,
которая сходится. Следовательно, сходится
ряд
,
которая сходится. Следовательно, сходится
ряд
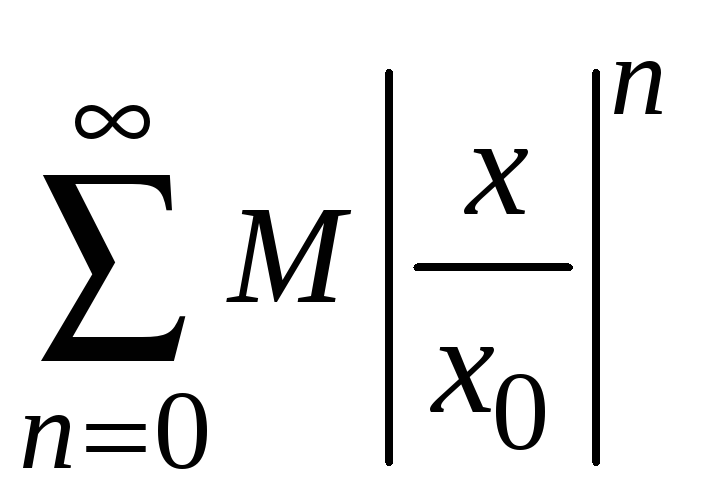 .
.
Ввиду того, что
члены ряда
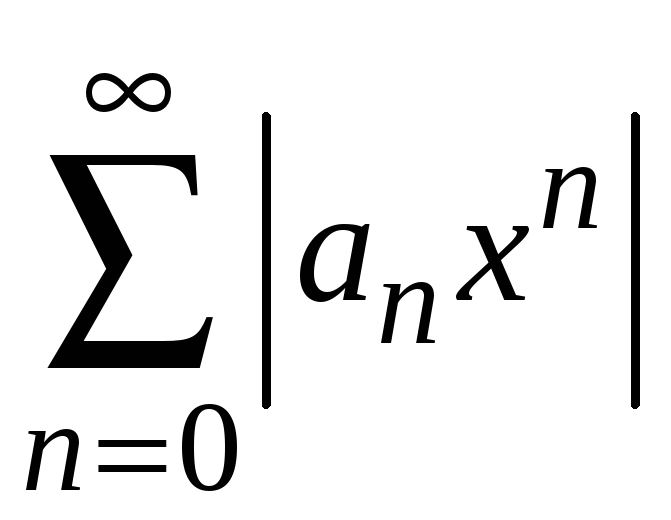 меньше соответствующих членов сходящегося
ряда
меньше соответствующих членов сходящегося
ряда
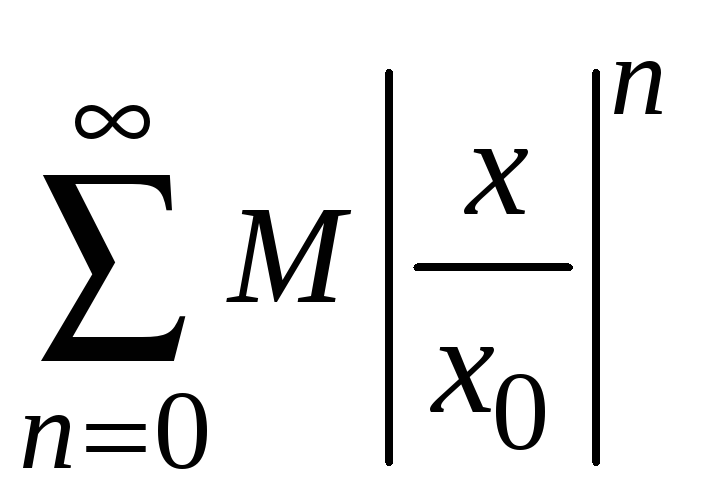 ,
по теореме 8.2 этот ряд сходится.
,
по теореме 8.2 этот ряд сходится.
В соответствии с
теоремой 8.8 об абсолютной сходимости
ряда сходится также исходный ряд
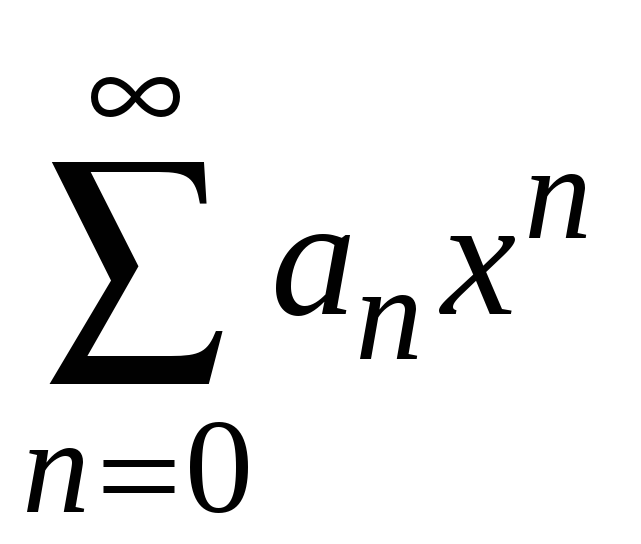 ,
причем абсолютно.
,
причем абсолютно.
2. Пусть теперь ряд
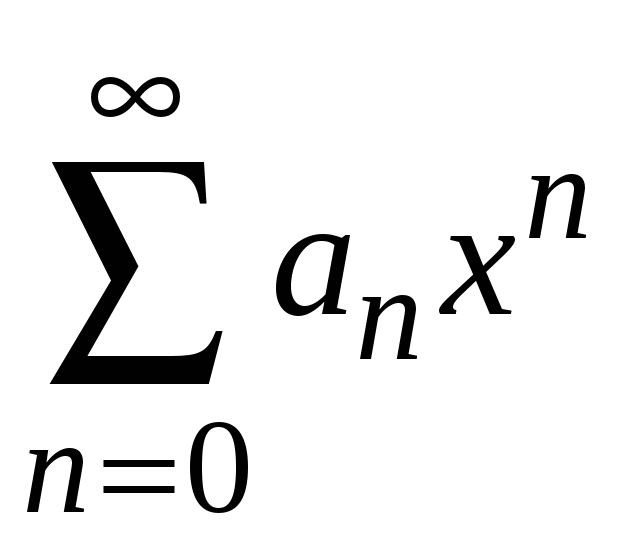 расходится при
расходится при
![]() ,
т. е. расходится ряд
,
т. е. расходится ряд
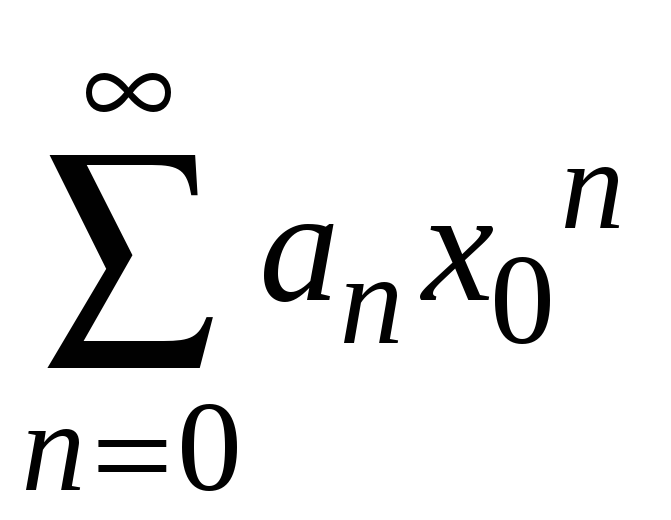 .
Докажем от противного, что при
.
Докажем от противного, что при
![]() ряд
ряд
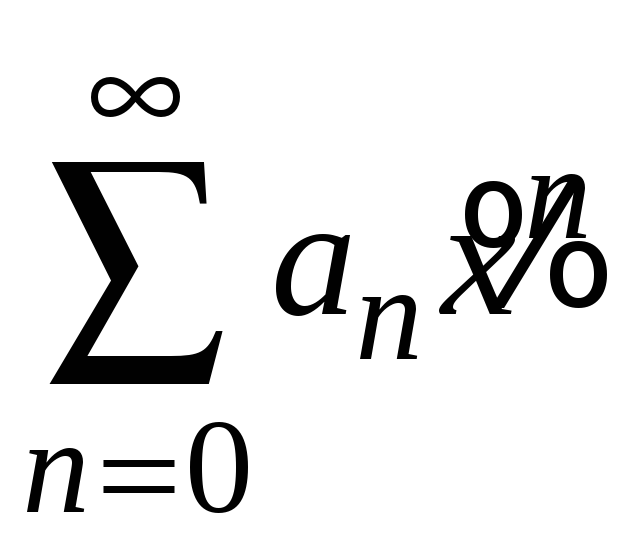 расходится. Предположим, что при
расходится. Предположим, что при
![]() исходный ряд сходится. Тогда по доказанному
в первой части настоящей теоремы он
должен сходится также и при меньших по
модулю значениях х,
т. е. при
исходный ряд сходится. Тогда по доказанному
в первой части настоящей теоремы он
должен сходится также и при меньших по
модулю значениях х,
т. е. при
![]() .
В этом и состоит противоречие.
.
В этом и состоит противоречие.
Теорема Абеля
является теоремой о виде области
сходимости степенного ряда, так как
если ряд сходится при
![]() ,
то он сходится и при
,
то он сходится и при
![]() ,
т. е. при
,
т. е. при
![]() .
Следовательно, область сходимости
симметрична относительно начала
координат (рис. 85).
.
Следовательно, область сходимости
симметрична относительно начала
координат (рис. 85).

Рис. 85
9.4. Радиус и область сходимости степенного ряда
Радиусом
сходимости
степенного ряда
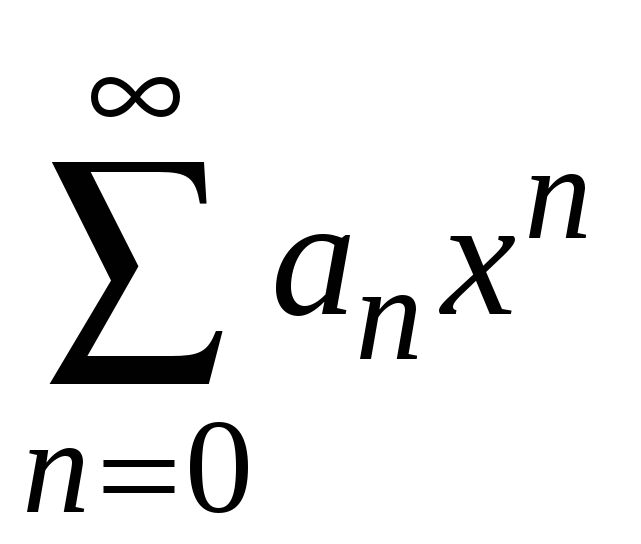 называется такое число R,
при котором ряд сходится, если
называется такое число R,
при котором ряд сходится, если
![]() ,
и расходится, если
,
и расходится, если
![]() .
.
Для нахождения
радиуса сходимости R
составим ряд из абсолютных величин
членов ряда
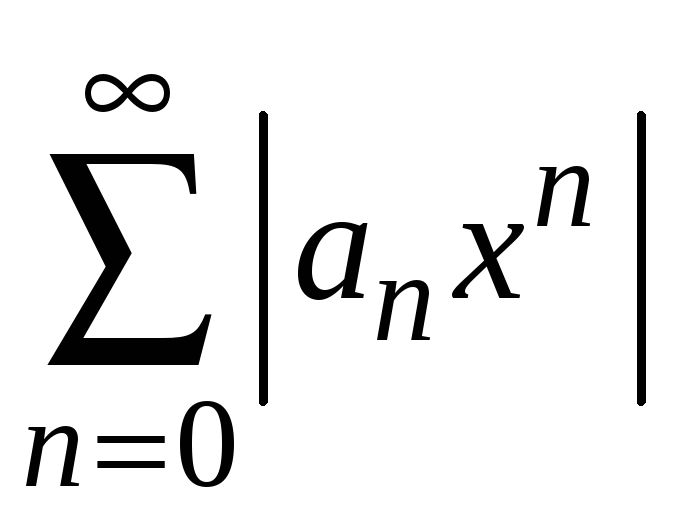 и применим признак Даламбера. Найдем
и применим признак Даламбера. Найдем
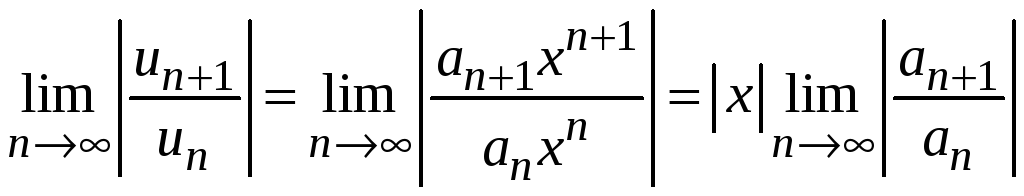 .
.
В соответствии с признаком Даламбера ряд сходится, если этот предел меньше единицы, т. е.
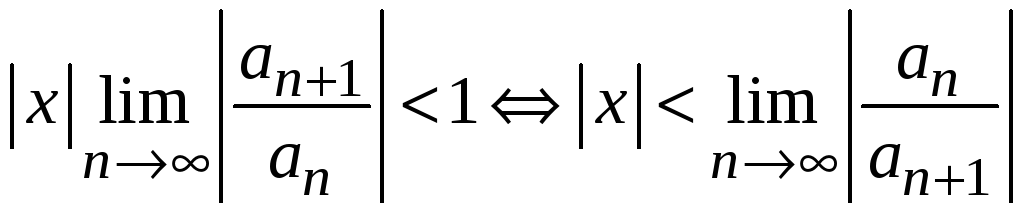 ,
,
и расходится, если
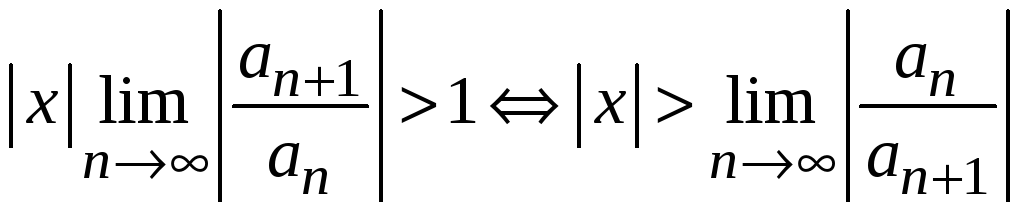 .
.
Отсюда следует, что радиус сходимости равен
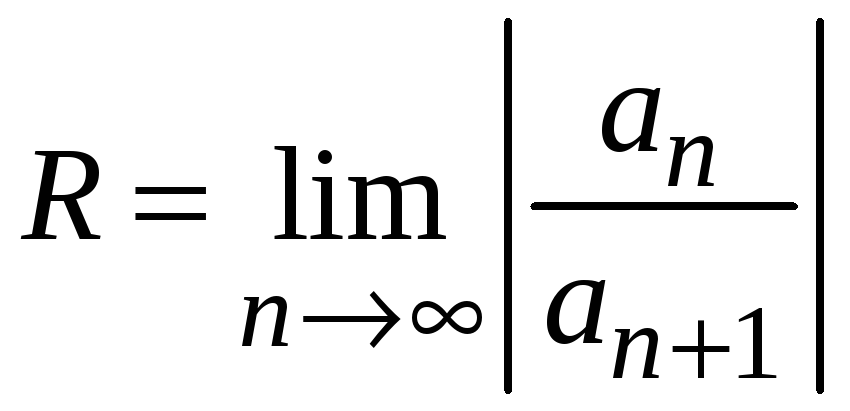 .
.
При использовании
данной формулы необходимо не забывать,
что в этой формуле
![]() и
и
![]() коэффициенты в членах степенного ряда
при х
в степени n
и n+1,
а не члены ряда.
коэффициенты в членах степенного ряда
при х
в степени n
и n+1,
а не члены ряда.
С помощью радиуса
сходимости можно найти интервал
сходимости ряда. При
![]() степенной ряд сходится. Для того чтобы
найти область сходимости, необходимо
дополнительно исследовать сходимость
ряда в граничных точках интервала
сходимости
степенной ряд сходится. Для того чтобы
найти область сходимости, необходимо
дополнительно исследовать сходимость
ряда в граничных точках интервала
сходимости
![]() .
.
Пример 9.1. Найти
область сходимости ряда
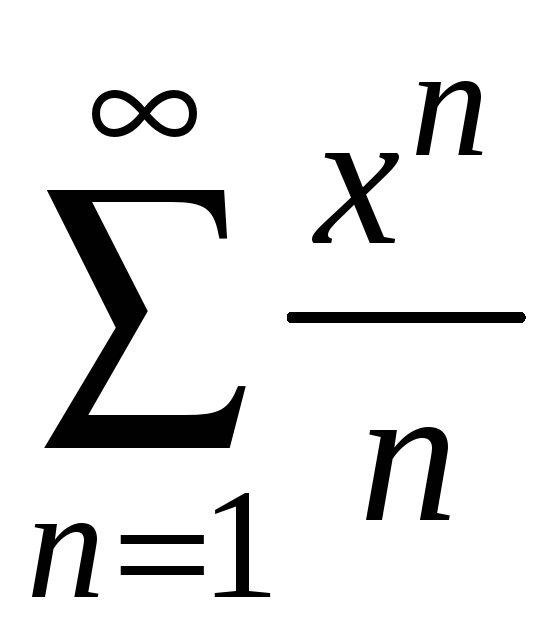 .
.
Находим радиус сходимости
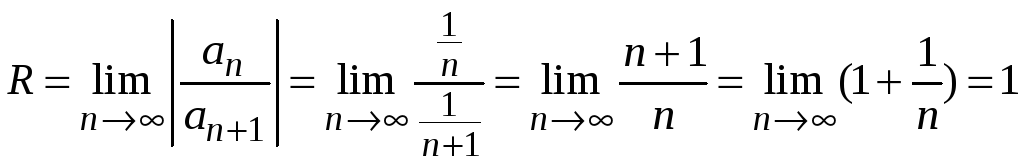 .
.
Интервал сходимости
ряда
![]() .
.
Исследуем сходимость ряда в граничных точках.
При
![]() ряд имеет вид
ряд имеет вид
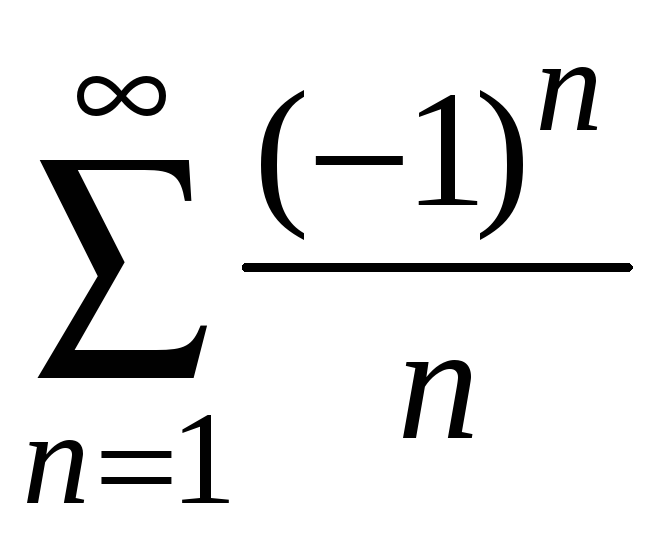 является знакочередующимся, его члены
монотонно убывают и стремятся к нулю.
По теореме Лейбница он сходится (см.
пример 8.15).
является знакочередующимся, его члены
монотонно убывают и стремятся к нулю.
По теореме Лейбница он сходится (см.
пример 8.15).
При
![]() ряд
ряд
![]() является гармоническим. Как известно
он расходится.
является гармоническим. Как известно
он расходится.
Следовательно,
область сходимости ряда
![]() .
.
Пример 9.2. Найти
область сходимости ряда
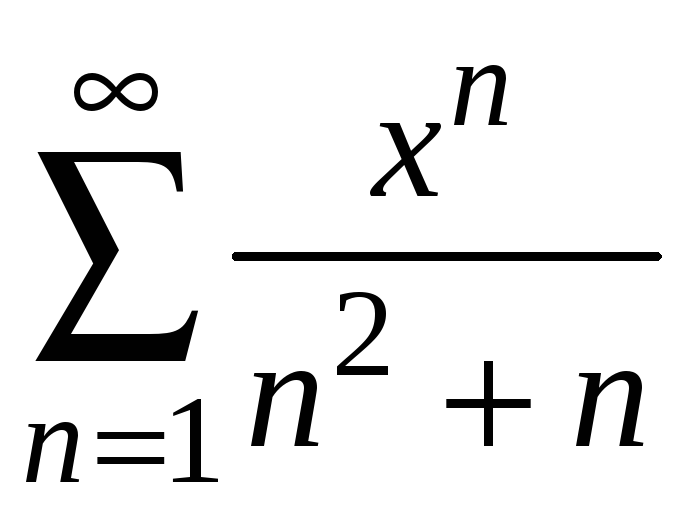 .
.
Находим радиус сходимости
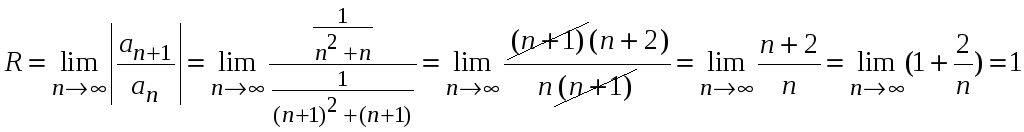 .
.
Интервал сходимости
![]() .
.
Исследуем сходимость ряда в граничных точках.
При
![]() ряд имеет вид
ряд имеет вид
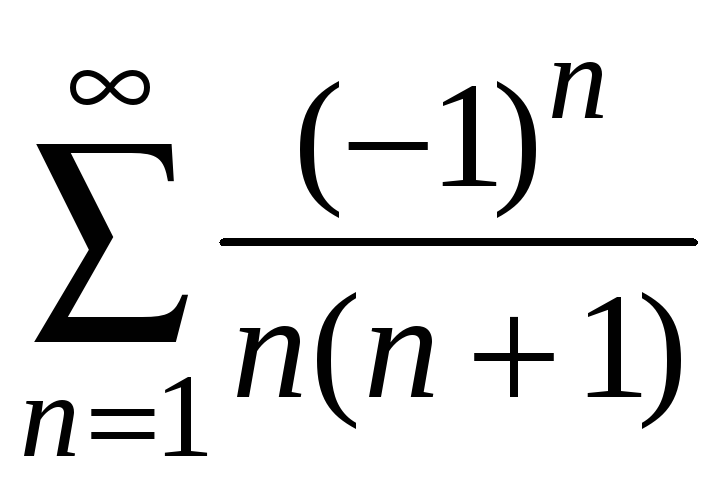 является знакочередующимся.
является знакочередующимся.
Члены ряда монотонно
убывают
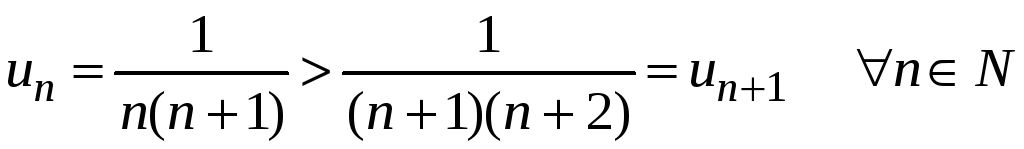
и стремятся к нулю
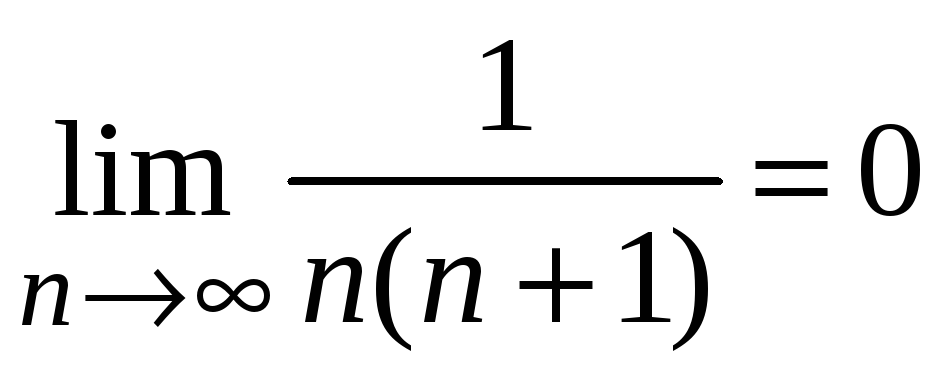 .
По теореме Лейбница ряд сходится.
.
По теореме Лейбница ряд сходится.
При
![]() ряд имеет вид
ряд имеет вид
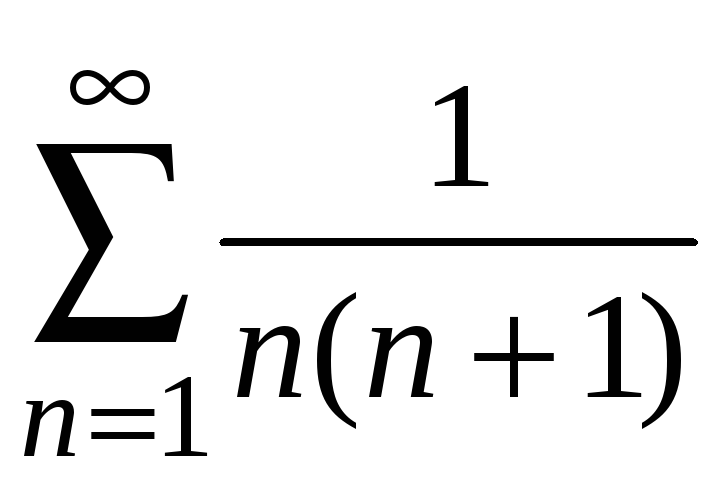 .
Его сходимость исследуем по интегральному
признаку Коши. Находим
.
Его сходимость исследуем по интегральному
признаку Коши. Находим
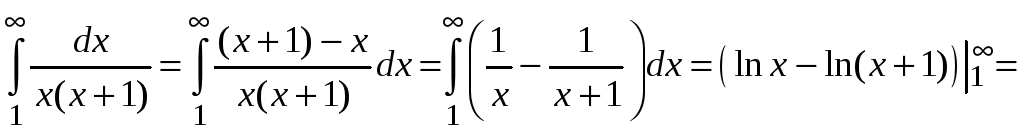
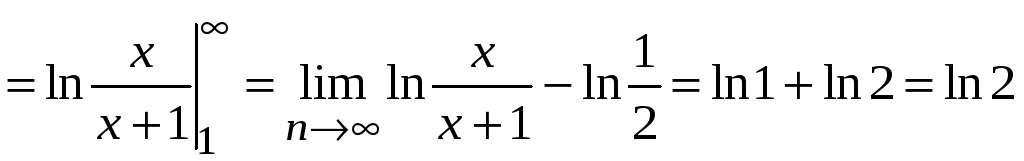 .
.
Интеграл сходится и ряд сходится.
Следовательно,
область сходимости ряда
![]() .
.
Пример 9.3. Найти
область сходимости ряда
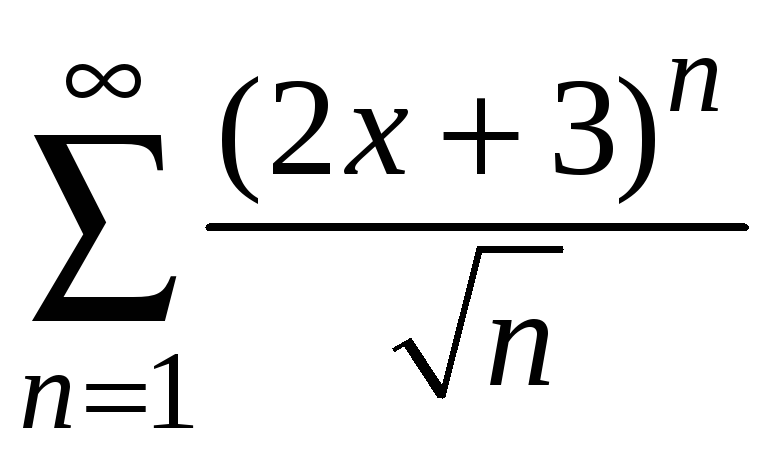 .
.
Введем новую
переменную
![]() ,
ряд примет вид
,
ряд примет вид
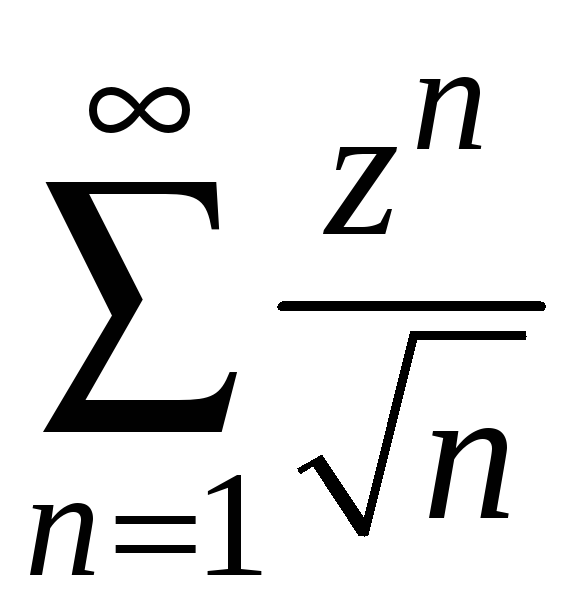 .
.
Найдем радиус сходимости этого ряда.
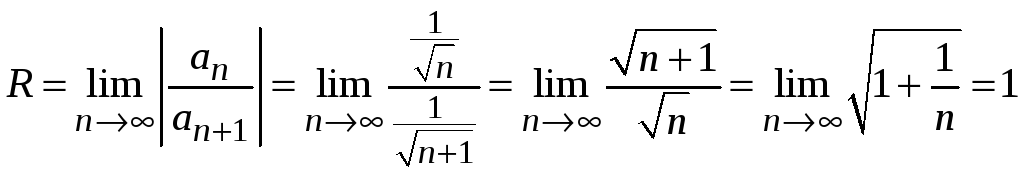 .
.
Интервал сходимости
ряда
![]() .
.
Исследуем сходимость ряда в граничных точках.
При
![]() ряд имеет вид
ряд имеет вид
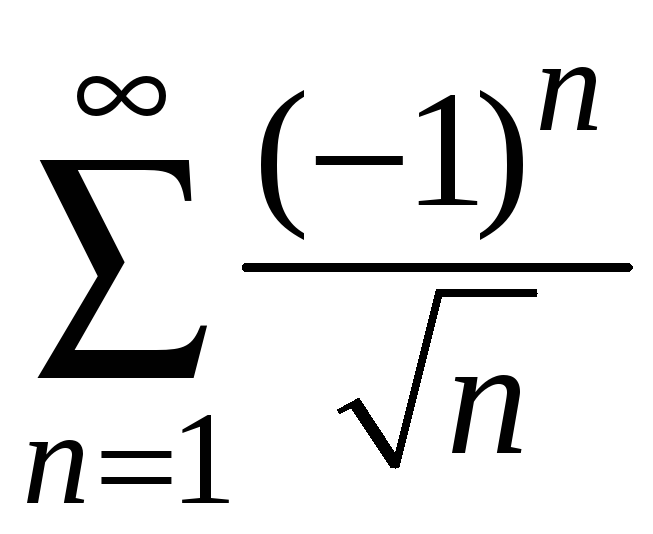 является знакочередующимся.
является знакочередующимся.
Члены ряда монотонно
убывают
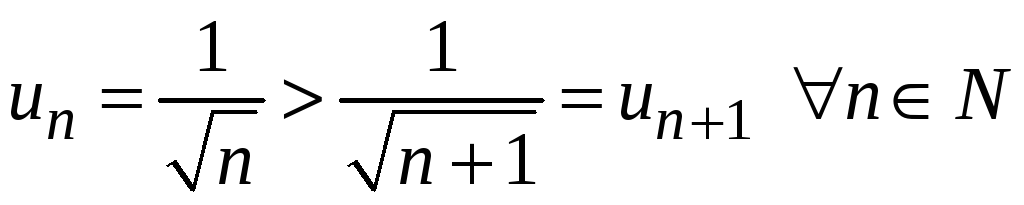
и стремятся к нулю
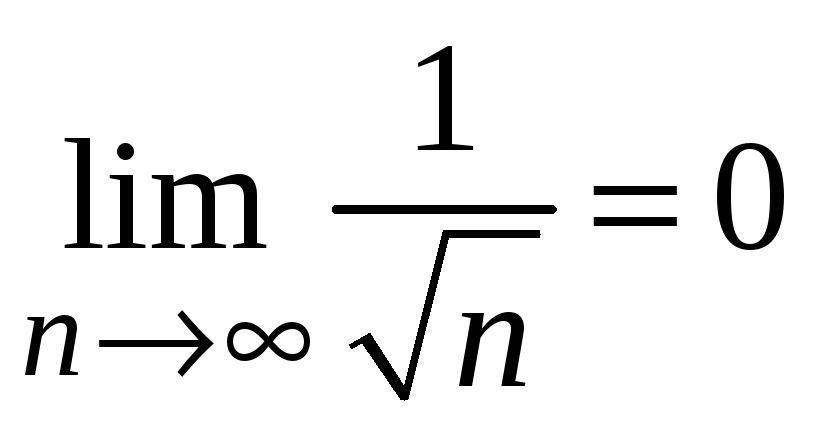 .
По теореме Лейбница ряд сходится.
.
По теореме Лейбница ряд сходится.
При
![]() ряд имеет вид
ряд имеет вид
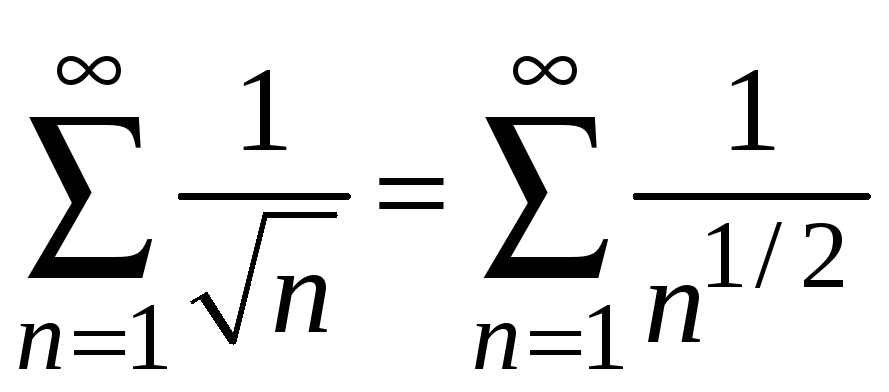 .
Ряд расходится, так как степень n
в знаменателе
.
Ряд расходится, так как степень n
в знаменателе
![]() (см. пример 8.12).
(см. пример 8.12).
Область сходимости
ряда
![]() .
Переходим к исходной переменной:
.
Переходим к исходной переменной:
![]()
Область сходимости
исходного ряда
![]() .
.
В отдельных случаях
степенные ряды могут содержать только
четные степени переменной
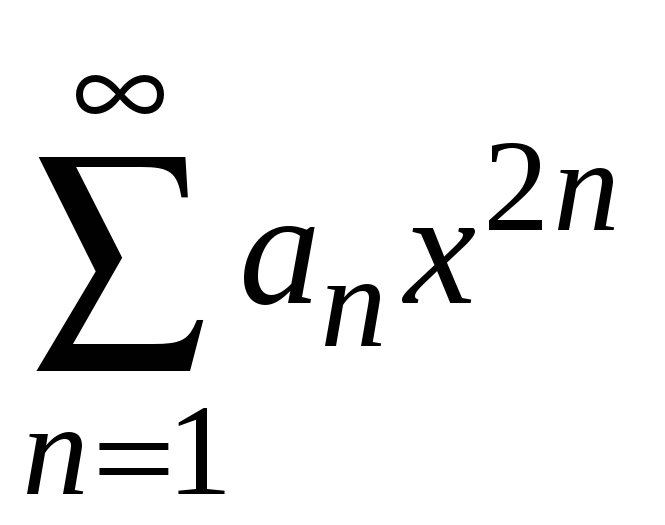 или нечетные степени
или нечетные степени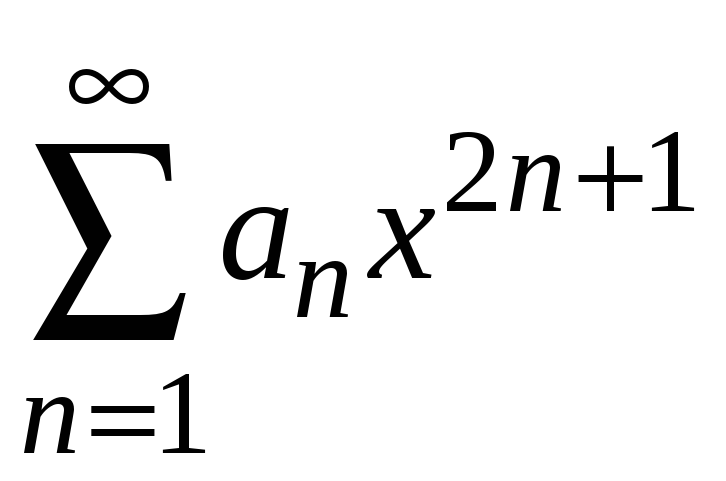 .
Для нахождения радиуса сходимости ряда
в таком случае составляется ряд из
абсолютных величин этого ряда, а затем
применяется признак Даламбера.
.
Для нахождения радиуса сходимости ряда
в таком случае составляется ряд из
абсолютных величин этого ряда, а затем
применяется признак Даламбера.
Для ряда с четными
степенями
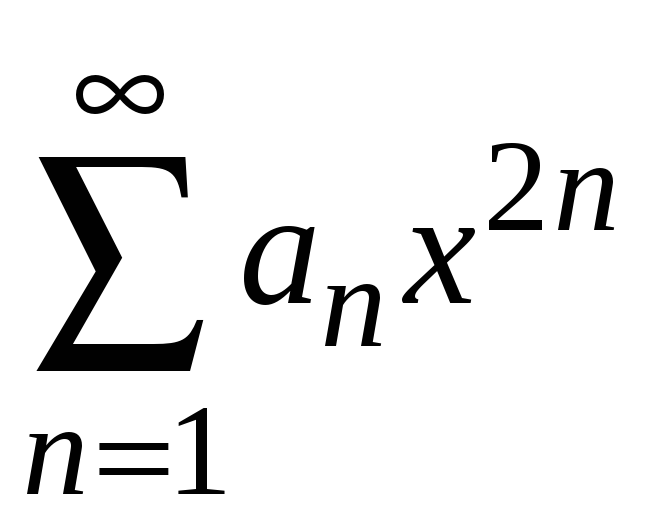 составляем
ряд
составляем
ряд
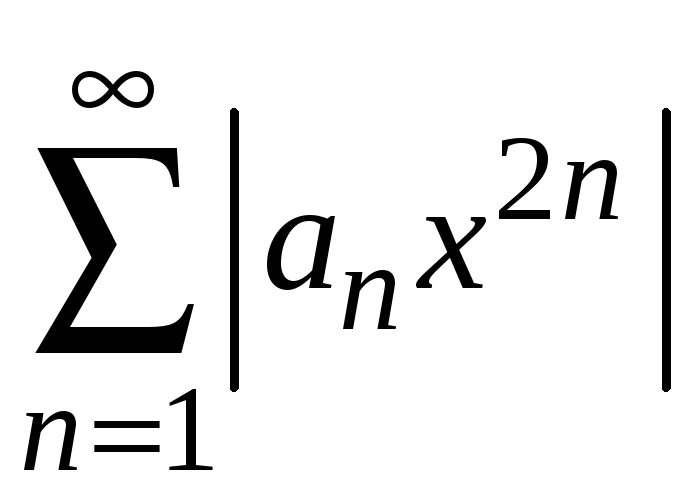 и применяем признак Даламбера
и применяем признак Даламбера
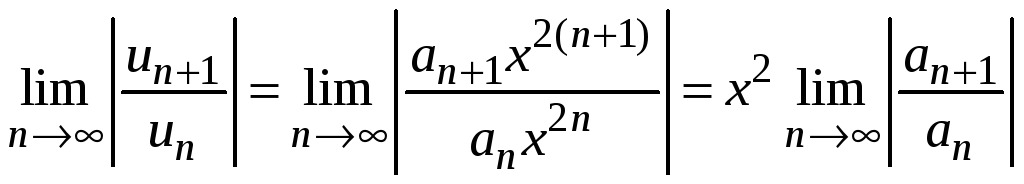 .
.
Ряд сходится, если
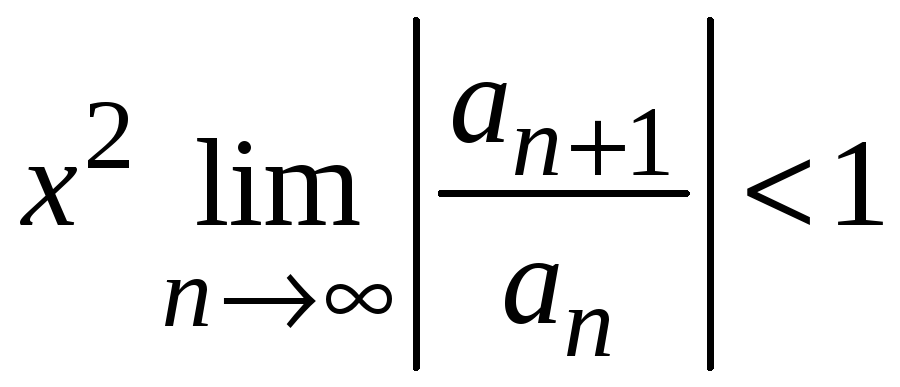 ,
т. е.
,
т. е.
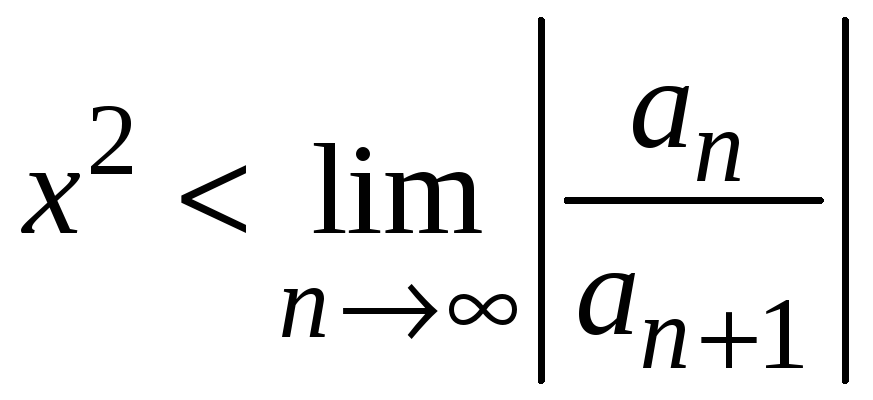 и расходится, если
и расходится, если
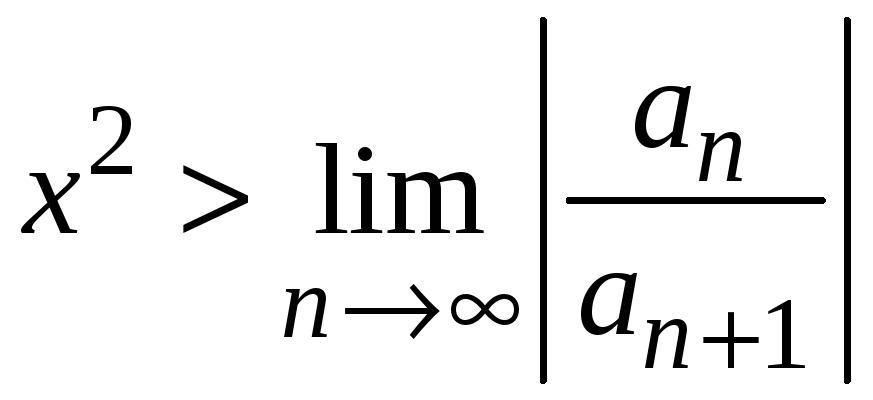 .
Следовательно, можно определить квадрат
радиуса сходимости такого ряда по
формуле
.
Следовательно, можно определить квадрат
радиуса сходимости такого ряда по
формуле
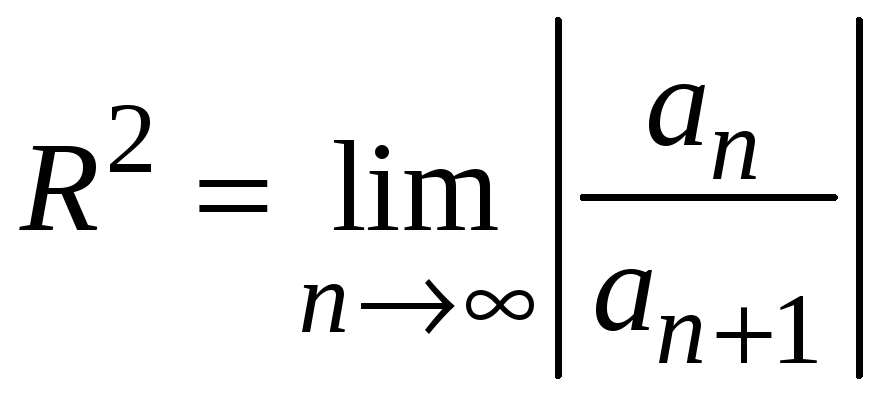 .
.
Для ряда с нечетными
степенями
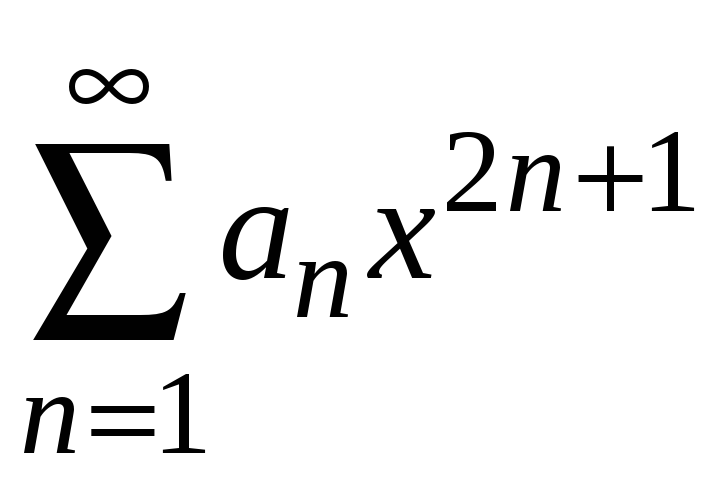 составляем ряд
составляем ряд
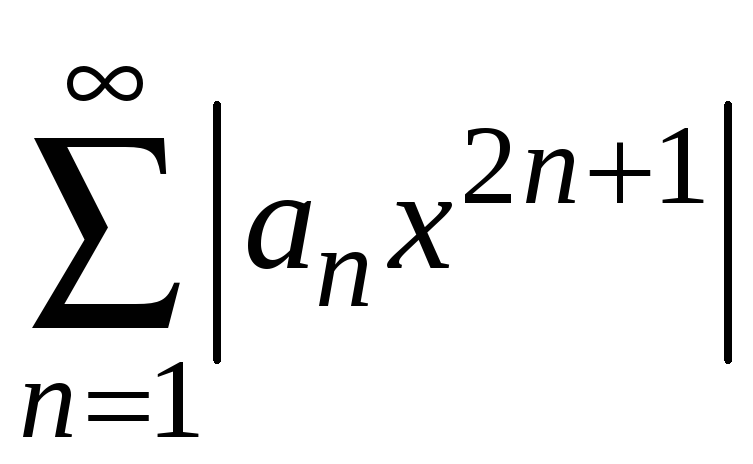 ,
применяем признак Даламбера
,
применяем признак Даламбера
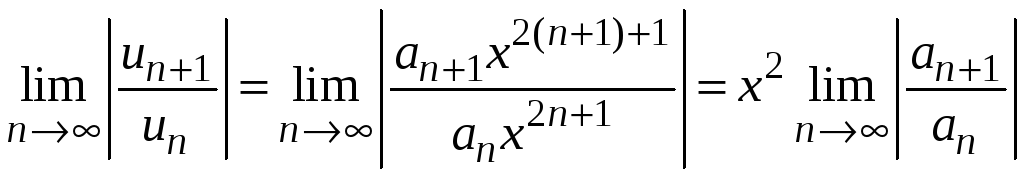 .
.
Ряд сходится, если
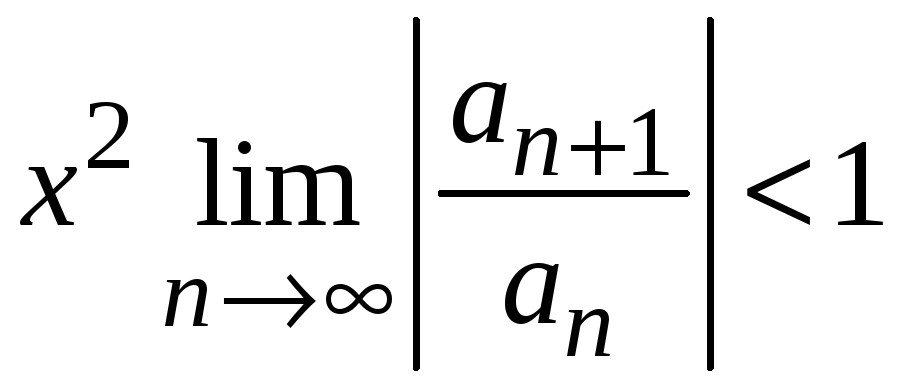
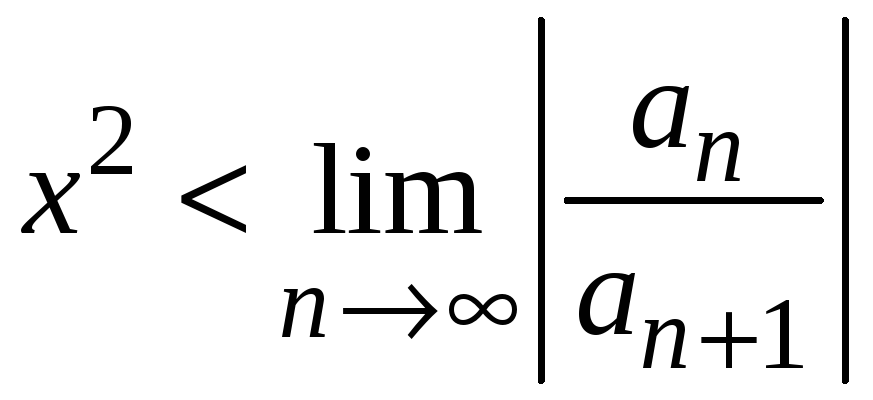 и расходится, если
и расходится, если
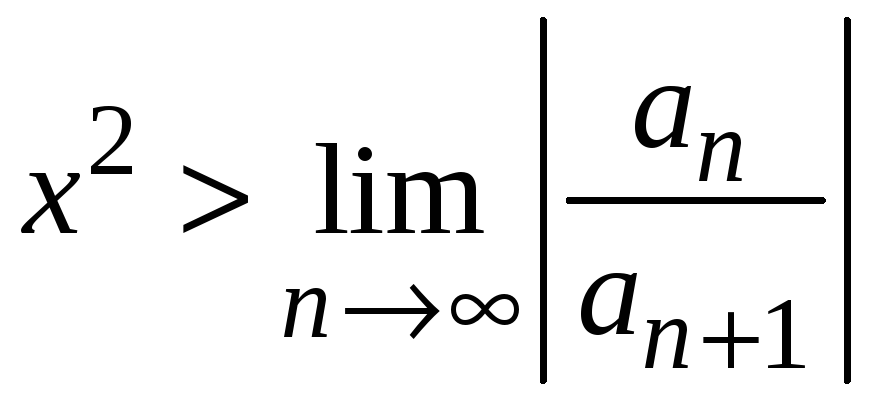 .
Следовательно, в случае ряда с нечетными
степенями справедлива та же формула
для квадрата радиуса сходимости.
.
Следовательно, в случае ряда с нечетными
степенями справедлива та же формула
для квадрата радиуса сходимости.
Пример 9.4. Найти
область сходимости ряда
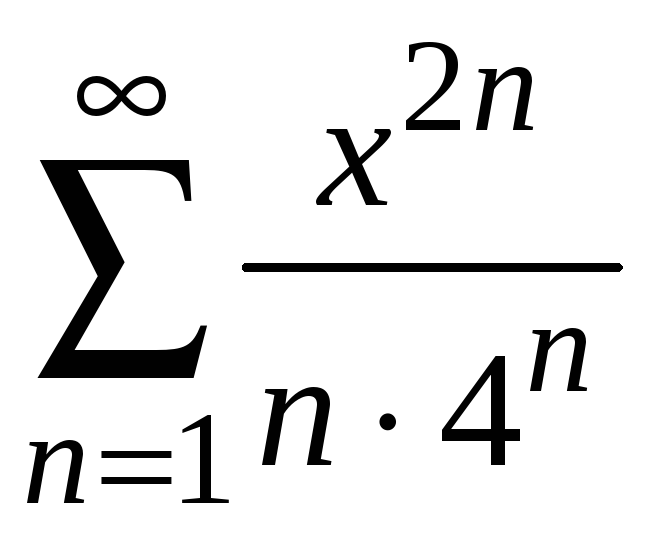 .
.
Находим
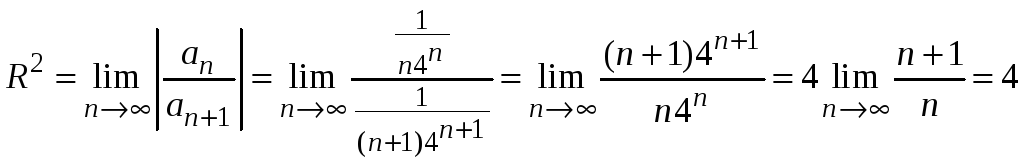 .
.
Радиус сходимости
![]() .
Интервал сходимости ряда
.
Интервал сходимости ряда
![]() .
.
При
![]()
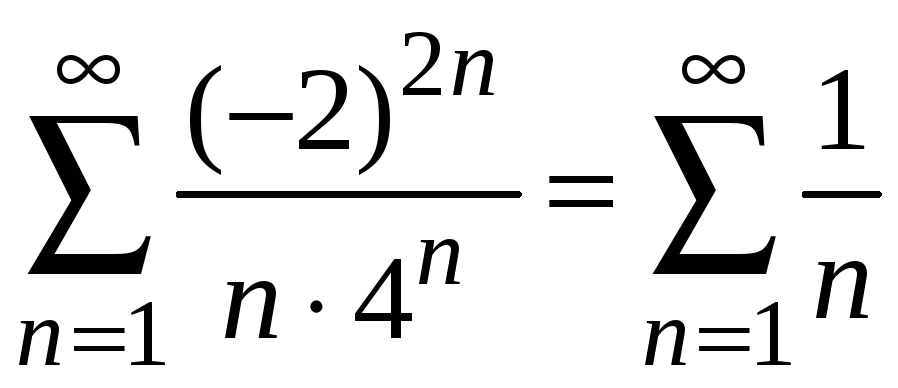 ряд расходится (гармонический).
ряд расходится (гармонический).
При
![]()
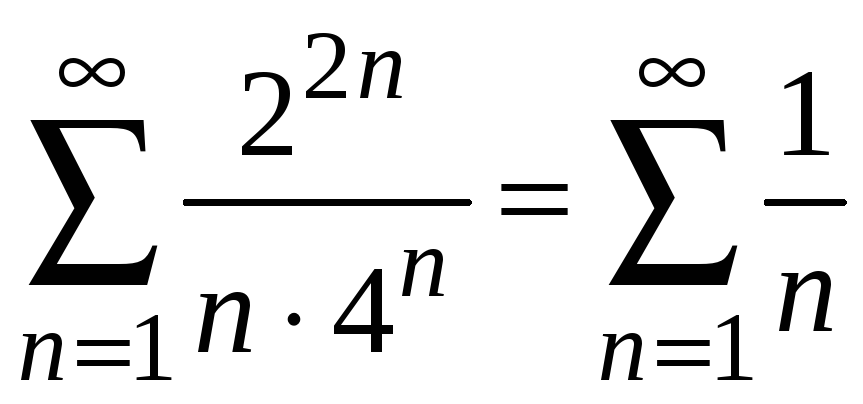 ряд расходится.
ряд расходится.
Область сходимости
ряда
![]() .
.
