7.7. Уравнение Бернулли

В общем случае уравнение Бернулли имеет вид

, ,

здесь  непрерывные функции.

Поделим уравнение на , получим

.

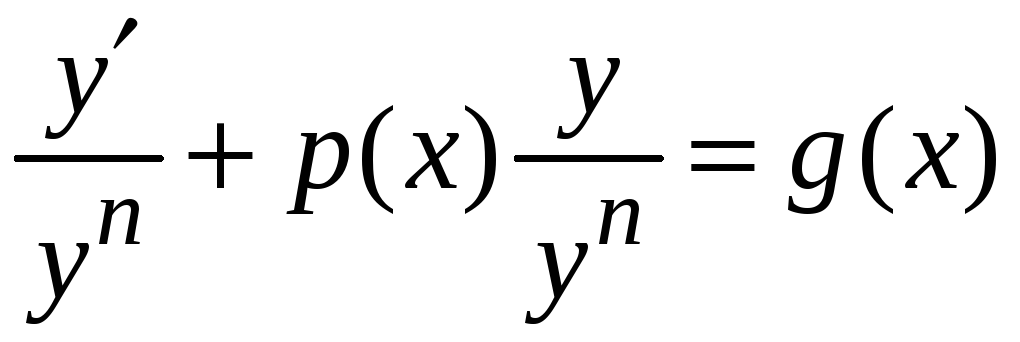Данное уравнение приводится к линейному уравнению с помощью подстановки

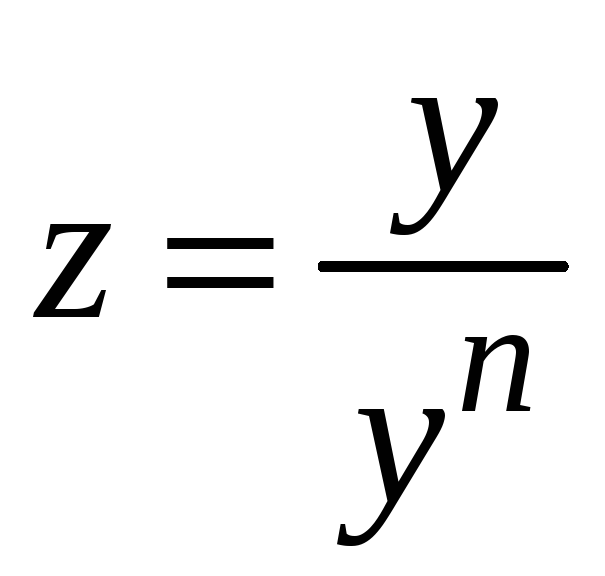или .

Найдем 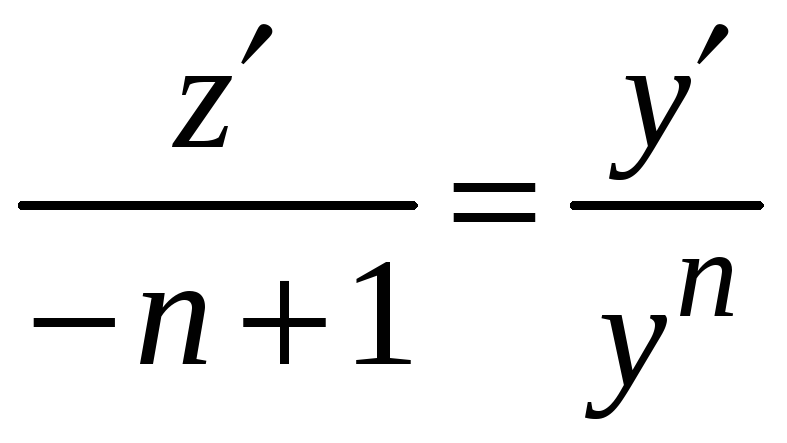 и подставим в исходное уравнение, получим линейное уравнение относительно переменной z.

.

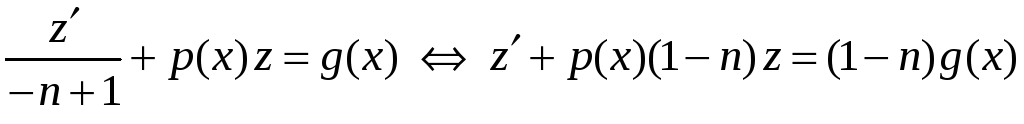Далее уравнение может быть разрешено известными методами решения линейного уравнения. Однако уравнение Бернулли может быть решено без замены переменной непосредственно с помощью подстановки .

Пример 7.14. Решить уравнение .

Используем подстановку .

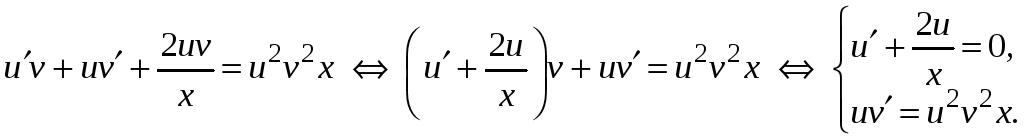
Решаем первое уравнение системы

.

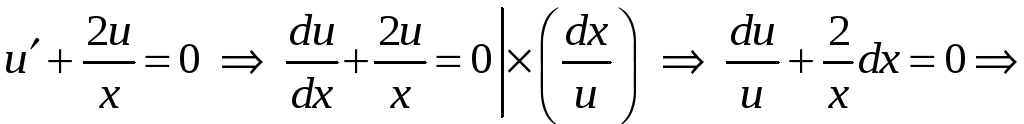
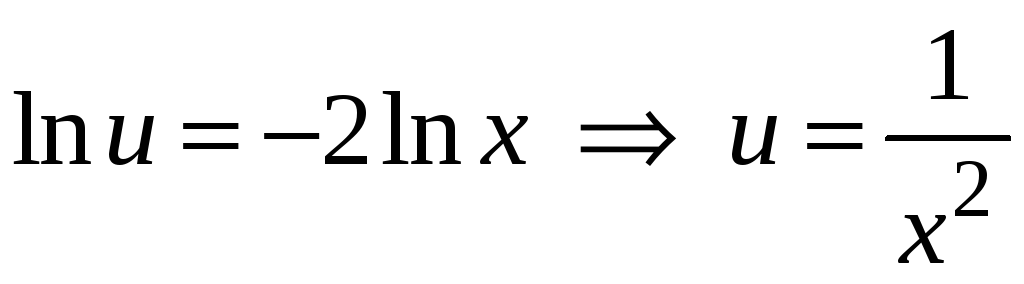Решаем второе уравнение системы

.

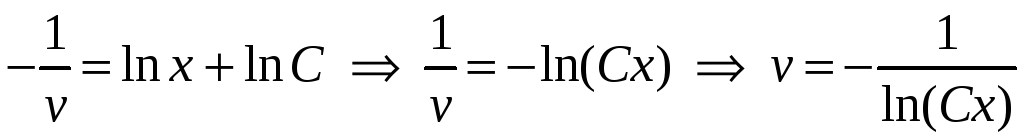Записываем решение исходного уравнения или

.

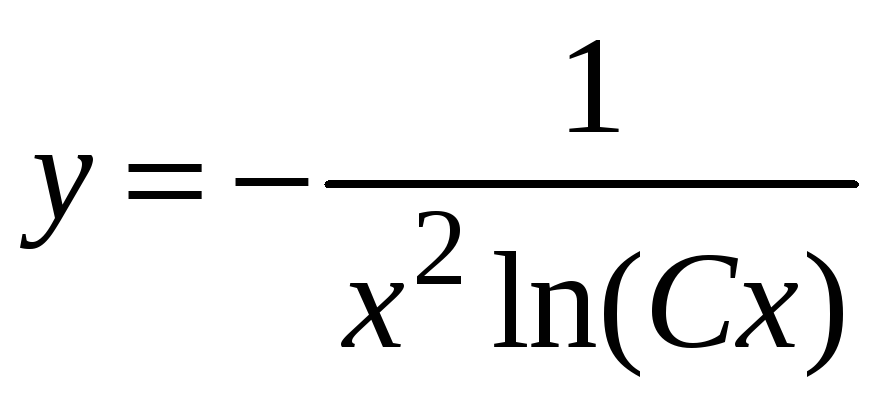7.8. Дифференциальные уравнения первого порядка в полных дифференциалах

Данные уравнения в общем случае имеют вид

,

где левая часть представляет полный дифференциал некоторой функции .

Известно, что полный дифференциал функции равен

.

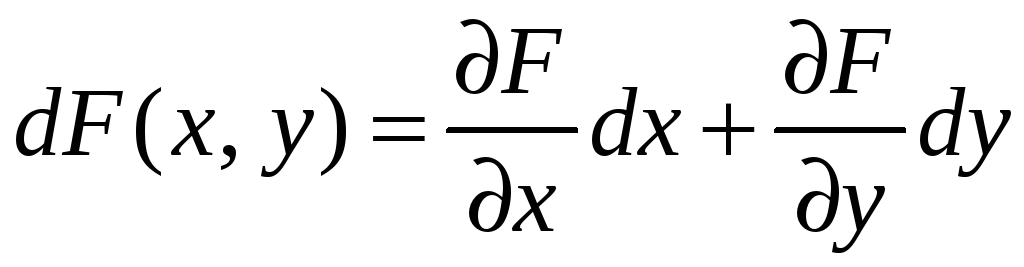Если левая часть заданного уравнения равна , то уравнение можно записать в виде . Тогда общий интеграл (общее решение в неявном виде) данного уравнения будет определяться уравнением , где С – произвольная постоянная.

Необходимым и достаточным условием того, чтобы выражение

являлось полным дифференциалом, служит равенство

.

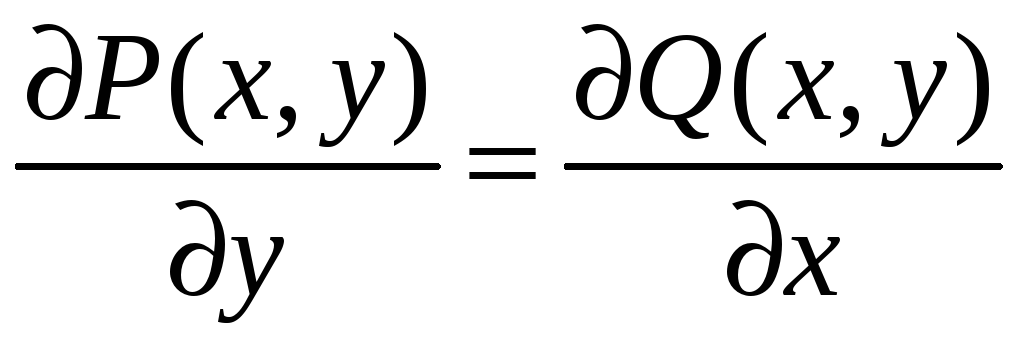Если это условие выполняется, то

.

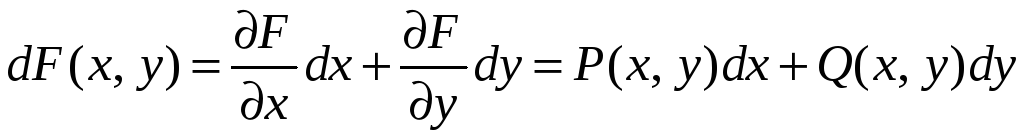Отсюда следует

.

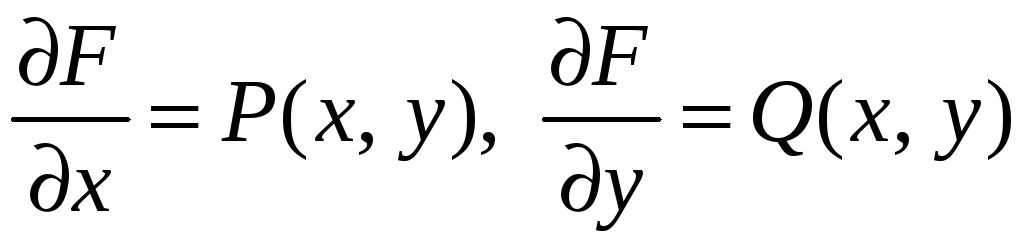Интегрируем соотношение по x, находим

,

где  произвольная функция, зависящая от y.

Функцию С(y) необходимо выбрать так, чтобы выполнялось второе условие существования полного дифференциала

.

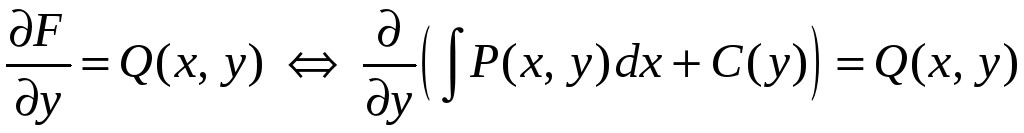Дифференцируем по y, имеем .

Отсюда получаем дифференциальное уравнение для нахождения функции С(y)

.

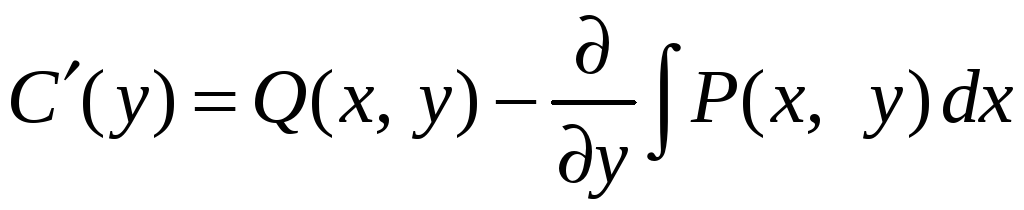Интегрируем данное уравнение, находим С(y) и подставляем его в ранее полученное выражение .

Получим общий интеграл

или .

Если имеются начальные условия для нахождения частного решения , то необходимо найти и записать частный интеграл .

Пример 7.15. Для уравнения найти общий интеграл и частный интеграл, удовлетворяющий условиям .

Проверим условие существования полного дифференциала. Находим

.

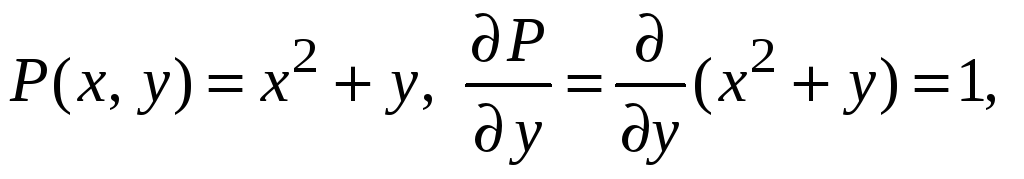
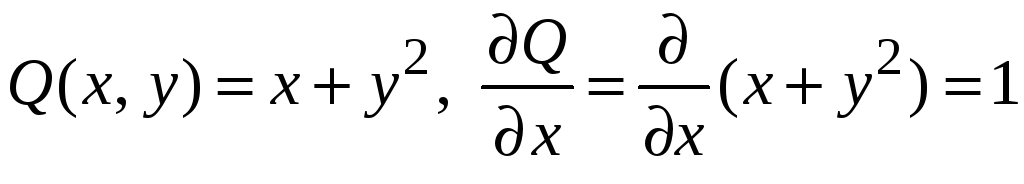Условие 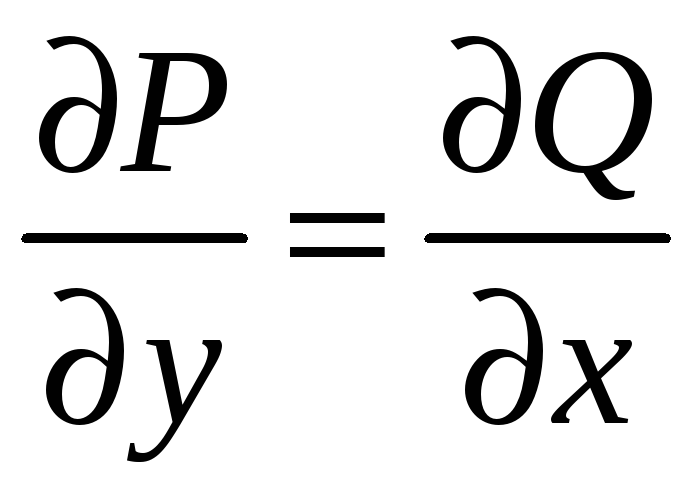выполняется 1 = 1.

Находим

.

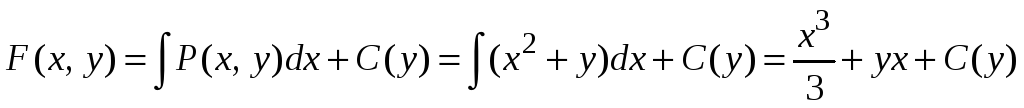Находим частную производную от этой функции

.

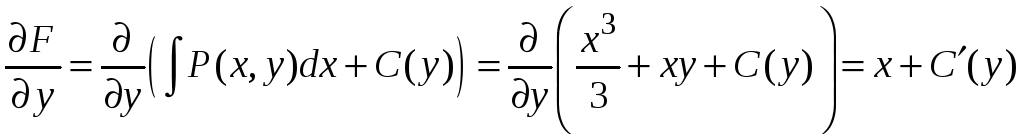Приравниваем к , получаем уравнение для нахождения .

,

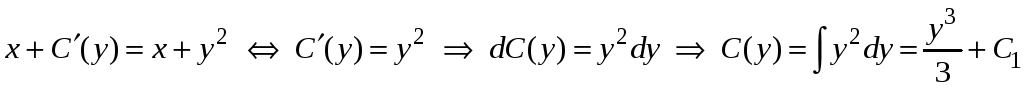где .

Записываем .

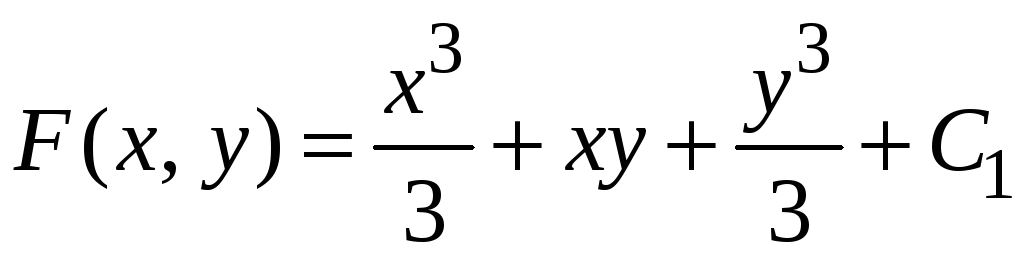Общий интеграл исходного уравнения имеет вид

, где ,

или

, где .

Находим значение произвольной постоянной С, соответствующее начальным условиям ,

.

Частный интеграл

.

Таким образом, общий и частный интегралы имеют вид

, .

7.9. Дифференциальные уравнения высших порядков

В общем случае дифференциальное уравнение n-ого порядка имеет вид

или .

Теорема 7.2 о существовании и единственности решения.

Если в дифференциальном уравнении функция и ее частные производные

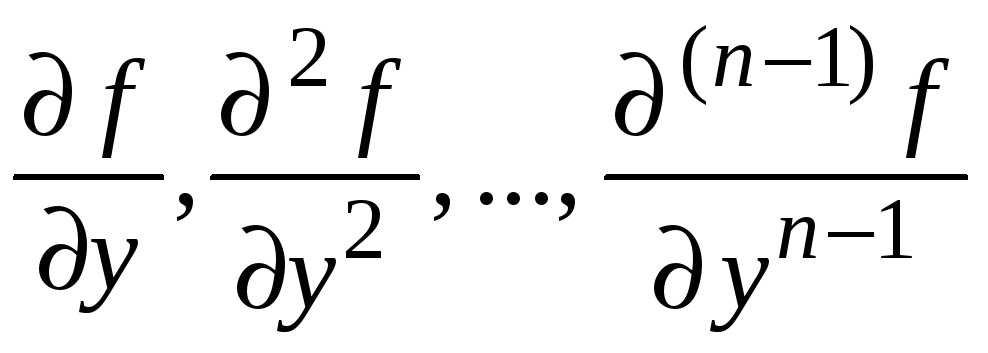
являются непрерывными в некоторой области D, то для любой точки , принадлежащей этой области, существует единственное решение уравнения, удовлетворяющее начальным условиям

.

Если условия данной теоремы выполняются, то геометрически решение дифференциального уравнения n-ого порядка представляет кривую, проходящую через точку в направлении .