7. 5. Однородные дифференциальные уравнения (дифференциальные уравнения с однородными функциями)

Функция называется однородной n-го измерения, если , где t – параметр.

Например, для функции находим

.

Следовательно, эта функция второго измерения (n = 2).

Покажем, что частное двух однородных функций и одного и тоже измерения есть однородная функция нулевого измерения. Действительно,

.

Однородными дифференциальными уравнениями называются уравнения вида

,

где и  однородные функции одного измерения.

Данное уравнение можно привести к уравнению с разделяющимися переменными. Для этого преобразуем уравнение

.

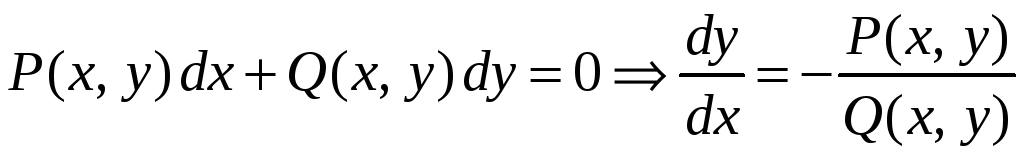Обозначим . Тогда уравнение примет имеет вид

,

где  однородная функция нулевого измерения, т. е.

.

Если принять параметр , то .

Уравнение сводится к уравнению с разделяющимися переменными с помощью подстановки

или ,

где u = u (x) функция от x.

Найдем производную и подставим ее в уравнение, получим

.

Разделим переменные и проинтегрируем

 .

Решение уравнения сведено к нахождению интегралов. В результате интегрирования будет получен общий интеграл . Для нахождения общего интеграла исходного дифференциального уравнения необходимо сделать обратную замену переменной , в результате которой общий интеграл будет иметь вид

.

Пример 7.10. Решить уравнение ; при х = 1 y = 1.

Используем подстановку . Находим и подставляем в уравнение. Получаем

.

Сгруппируем отдельно слагаемые с и

.

Разделим переменные и проинтегрируем

.

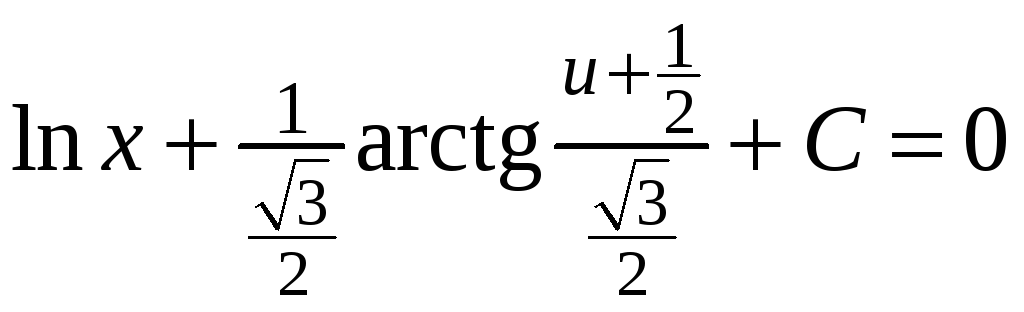Выполним обратную подстановку , запишем общий интеграл

.

Найдем значение произвольной постоянной С, соответствующее начальным условиям .

.

Запишем частное решение

.

Пример 7.11. Решить уравнение ; при х = 1 .

Используем подстановку . Найдем . Подставим y и в уравнение, получим

.

В этом уравнении сгруппируем в одном слагаемом , а в другом все остальные слагаемые, получим

.

Учитываем, что , имеем

.

Разделим переменные и проинтегрируем

.

Получаем

 .

Выполняем обратную замену переменной , получаем общий интеграл

.

Находим значение произвольной постоянной.

При получим  .

Записываем частное решение

.

7.6. Линейные дифференциальные уравнения первого порядка

Данные уравнения в общем случае имеют вид

,

где  непрерывные функции.

Разделим уравнение на , получим

,

где .

Известны два метода решения этих уравнений.

1. Метод замены переменной.

Искомую функцию заменяют на произведение двух функций

,

где ,  некоторые неизвестные дифференцируемые функции.

Подставим в уравнение, получим . Третье слагаемое сгруппируем с одним из первых слагаемых, либо с , либо с . Функции и входят в уравнение замены симметрично. Пусть объединим первое и третье слагаемые

.

Искомой является одна функция , а введены с помощью замены две , , поэтому одну из них, пусть , выберем по своему усмотрению так, чтобы равнялось нулю. Тогда уравнение распадется на два уравнения, каждое из которых с разделяющимися переменными,

Необходимо сначала решить первое уравнение, найти функцию . Затем подставить эту функцию во второе уравнение и решить его.

Решаем первое уравнение. При решении этого уравнения достаточно найти не общее решение, а одно какое-либо частное решение

  .

Подставим найденную функцию во второе уравнение и решим его. Найдем функцию .

.

Затем записываем решение исходного уравнения как произведение функций .

.

Получена конечная формула для нахождения общего решения линейного уравнения. Однако, при решении примеров, обычно, используют замену и повторяют приведенные выше действия.

Пример 7.12. Решить уравнение .

Используем подстановку , получаем

Решаем первое уравнение системы

.

Решаем второе уравнение системы .

 .

Интеграл находим методом интегрирования по частям

 .

Находим общее решение исходного уравнения ;

.

2. Метод вариации произвольной постоянной.

Для нахождения общего решения неоднородного линейного уравнения

сначала решают соответствующее однородное уравнение

.

Данное уравнение с разделяющимися переменными. Решая его, получим

 

.

Далее, произвольную постоянную заменяют на функцию и ищут решение исходного неоднородного уравнения в виде

.

Теперь, чтобы получить решение уравнения, необходимо найти функцию . Найдем производную функции .

.

Подставим функцию и ее производную в исходное неоднородное уравнение .

.

Второе и третье слагаемые в левой части этого уравнения уничтожаются, получается дифференциальное уравнение относительно функции с разделяющимися переменными

.

Разделяем переменные и интегрируем

,

где С – произвольная постоянная.

Записываем решение исходного неоднородного уравнения

.

Пример 7.13 . Найти общее решение уравнения .

Используем метод вариации произвольной постоянной. Решим соответствующее исходному однородное уравнение

.

Ищем решение исходного неоднородного уравнения в виде . Подставляем эту функцию в исходное уравнение

.

Получаем уравнение для нахождения

.

Решаем это уравнение

.

Находим

.

Записываем решение исходного уравнения

или

.