3.17. Формула Тейлора для функций двух переменных

Теорема 3.6. Если в некоторой -окрестности точки функция непрерывна и имеет непрерывные частные производные до (n1)-го порядка включительно, то для любой точки этой окрестности справедлива формула

,

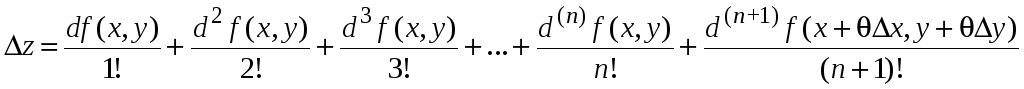где .

Д о к а з а т е л ь с т в о. Для доказательства используем формулу Маклорена для функции одной переменной, которая имеет вид

.

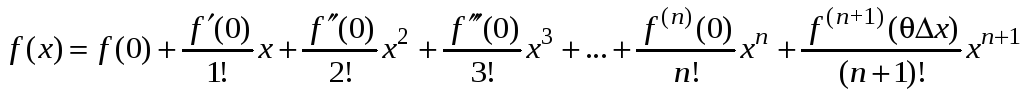Введем в рассмотрение новую функцию, которая зависит от t

.

Составим для нее формулу Маклорена. Для этого найдем ее производные как сложной функции.

.

.

Далее аналогично можно получить

,

.

Найдем значения функции и ее производных при t = 0:

, ,…, , .

Запишем формулу Маклорена

.

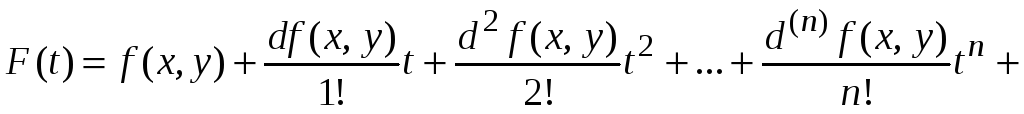
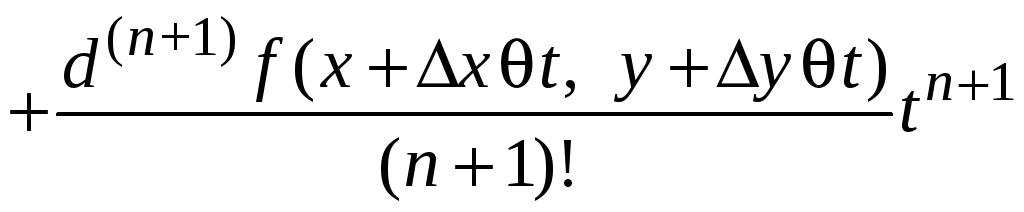При t = 1 . Формула примет вид

.

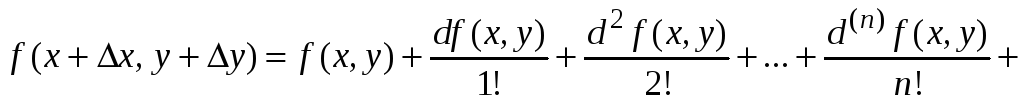
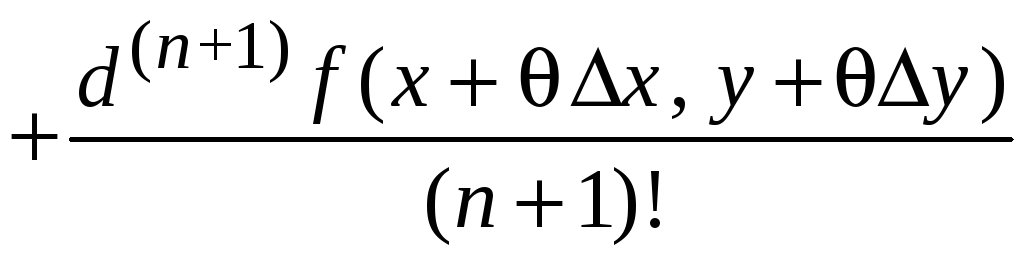Учитывая, что , формулу Маклорена можно записать в виде

.

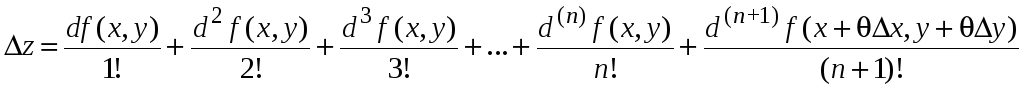В частном случае при n = 0 формула принимает вид

или

.

Эта формула является обобщением формулы Лагранжа на случай функции двух переменных.

3.18. Локальный экстремум функции нескольких переменных

Точка называется точкой локального максимума (минимума) функции , если существует некоторая окрестность этой точки такая, что для любой точки этой окрестности () (рис. 49).

Рис. 49

3.19. Необходимый признак локального экстремума

Теорема 3.7. Если точка является точкой экстремума функции , то частные производные в этой точке либо равны нулю, т. е.

,

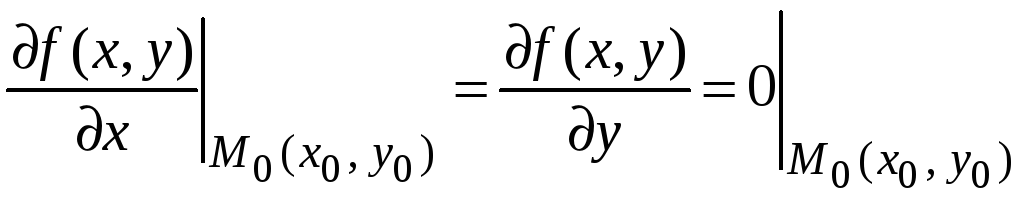либо не существуют.

Д о к а з а т е л ь с т в о. Пусть точка является мочкой максимума функции , т. е. существует -окрестность этой точки такая, что . При в этой окрестности , поэтому точка является также точкой максимума функции одной переменной х. По необходимому признаку локального экстремума функции одной переменной производная в этой точке либо не существует, либо равна нулю, т. е.

.

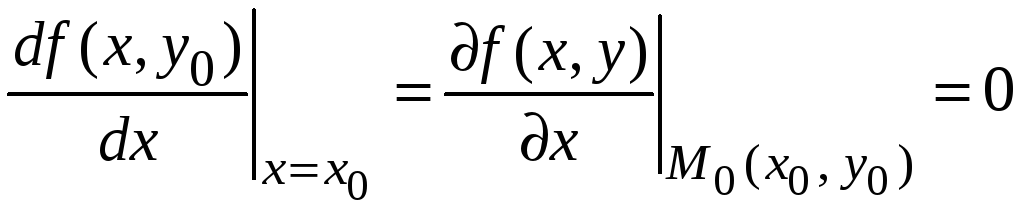Аналогично рассуждая, можно показать, что частная производная функции по y так же либо равна нулю, либо не существует.

3.20. Достаточный признак локального экстремума функции двух переменных

Теорема 3.8. Если функция в окрестности точки является непрерывной и имеет непрерывные частные производные до второго порядка включительно, и частные производные первого порядка в этой точке равны нулю, т. е.

,

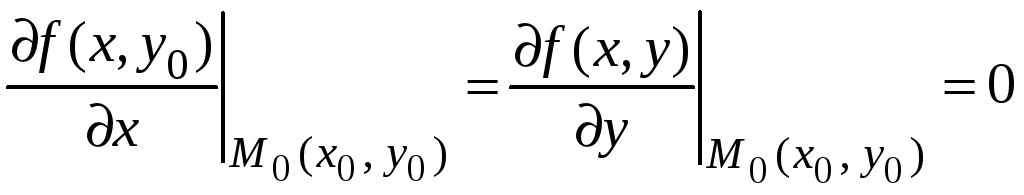то:

1) если , ,

где , , ,

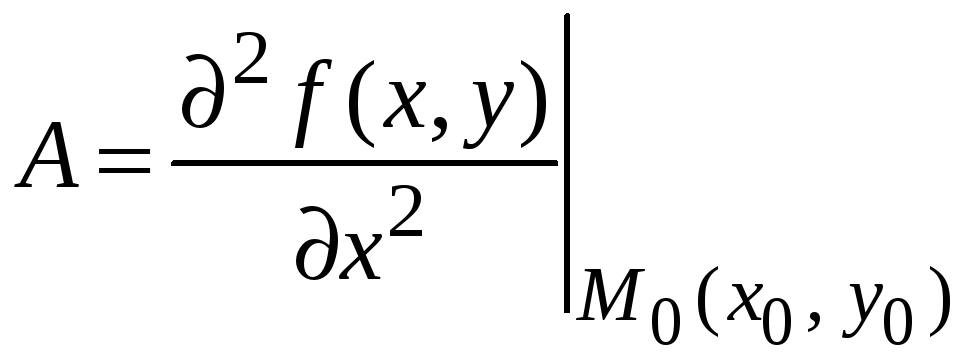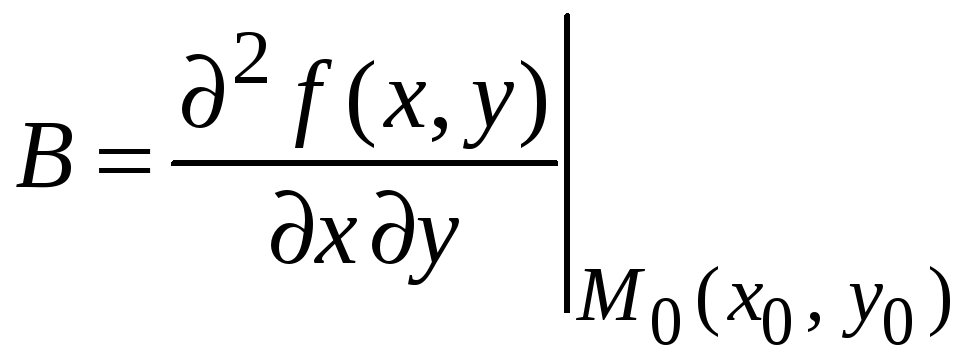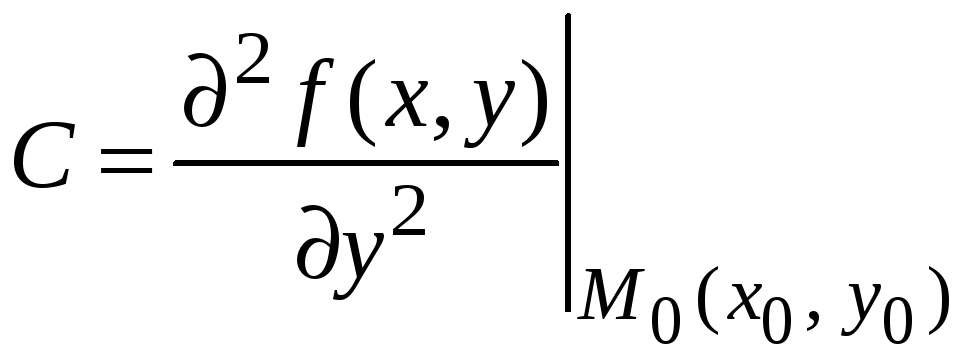то является точкой минимума;

2) если , то является точкой максимума;

3) если , то не является точкой экстремума;

4) если , то данный признак не позволяет решить вопрос об экстремуме функции в этой точке (требуются дополнительные исследования).

Д о к а з а т е л ь с т в о. Судить о поведении функции в некоторой окрестности точки будем по знаку величины приращения функции в этой точке. Если полное приращение функции для любой точки окрестности больше (меньше) нуля , то  точка минимума (максимума) (рис. 49).

Согласно формуле Тейлора приращение функции равняется

,

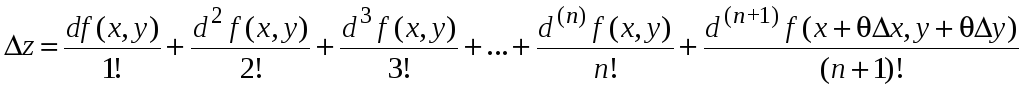где .

По условию теоремы частные производные первого порядка в точке равны нулю, т. е. эта точка является стационарной. Поэтому

.

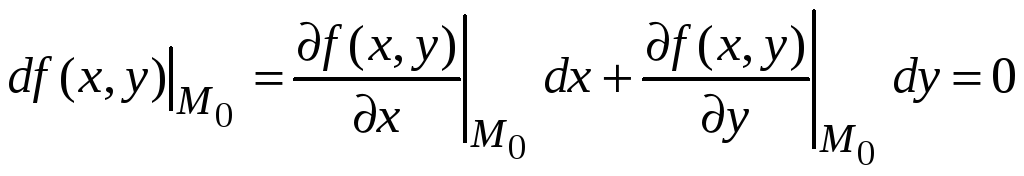Тогда в первом приближении с учетом только одного первого отличного от нуля слагаемого в точке равно .

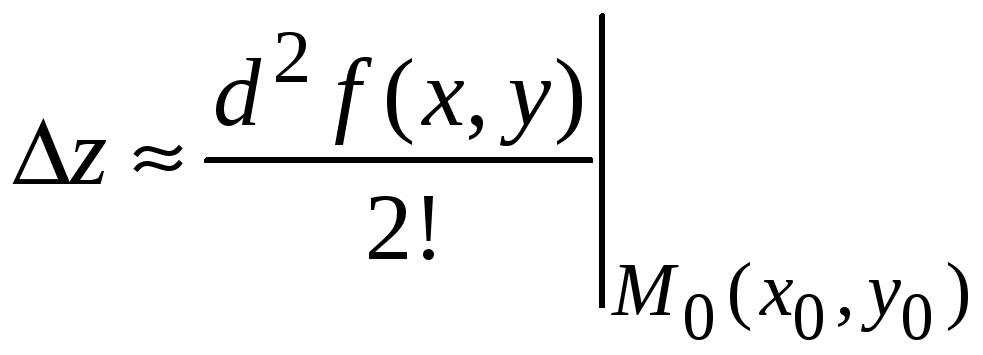Запишем более подробно дифференциал второго порядка

.

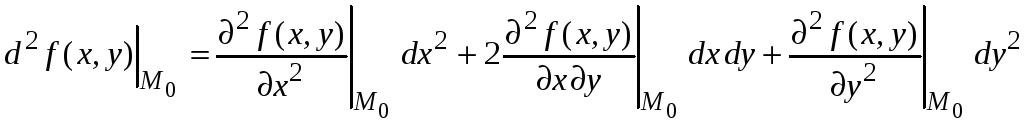Данный дифференциал представляет собой квадратичную форму относительно дифференциалов независимых переменных . Его можно записать в виде

.

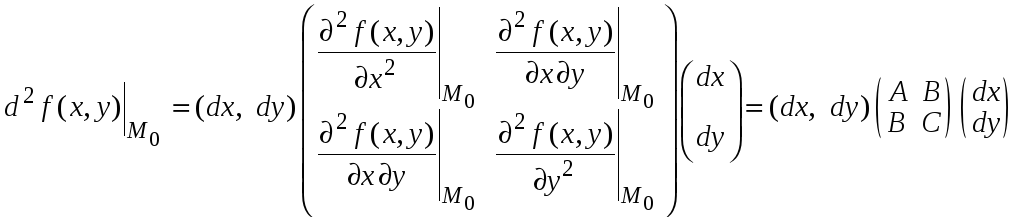По критерию Сильвестра квадратичная форма является определенно положительной, если все ее главные миноры положительные, т. е.

.

В этом случае 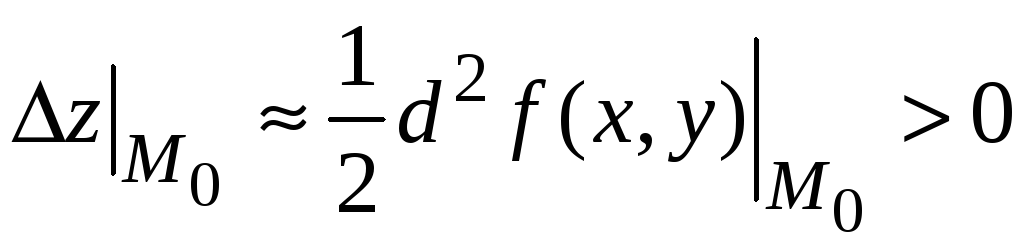, т. е. выполняются условия локального минимума в точке



.

Если , то .

Тогда точка будет являться точкой локального максимума. Следовательно, для того, чтобы в точке был максимум дифференциал должен быть отрицательным . Согласно критерию Сильвестра данная квадратичная форма будет отрицательно определенной, если

.

Если для квадратичной формы минор второго порядка , то квадратичная форма, а следовательно и приращение функции не являются знакоопределенными в окрестности точки и эта точка не является точкой локального экстремума.

Если же , в точке равен нулю, то знак приращения будет определяться дифференциалом третьего порядка , который является более высокого порядка малости по сравнению с . Для решения вопроса об экстремуме функции в этом случае необходимы дальнейшие исследования.

Пример 3.24. Исследовать на экстремум функцию .

Находим критические точки. Для этого согласно необходимому признаку экстремума, находим частные производные первого порядка, приравниваем их нулю и решаем систему.

   

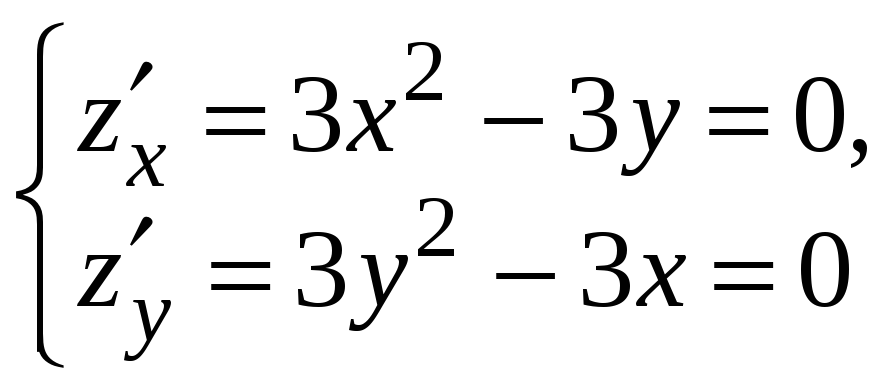
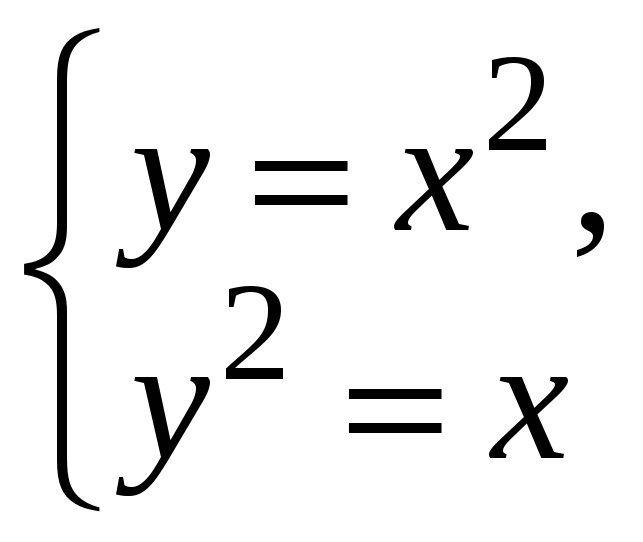
Имеется две критические точки и .

Используем достаточный признак для исследования этих точек на экстремум.

Находим , , .

Для точки находим , , ;

.

Следовательно, не является точкой экстремума.

Для точки находим , , ;

.

Так как , в точке имеет место минимум. Находим значение функции в этой точке .

Ответ: в точке .