3.15. Производная функции по направлению

Пусть функция непрерывная и дифференцируемая, вектор задает направление. Пусть имеется точка и в направлении от нее точка (рис. 48).

Рис. 48

Вектор имеет координаты , , , т. е. .

Модуль вектора , , , .

Косинусы cos, cos, cos называются направляющими косинусами вектора . Если вектор единичный , то и его координатами являются направляющие косинусы, т. е. .

Производной функции по направлению вектора в точке называется предел отношения приращения функции в этом направлении к приращению длины (модуля) вектора , при стремящемся к нулю , т. е.

.

Находим

.

Таким образом, получена формула дифференцирования функции по направлению вектора

.

Пример 3.21. Вычислить производную функции в точке по направлению вектора .

Находим , .

.

.

3.16. Градиент функции, его свойства

Градиентом функции называется вектор

,

где  единичные векторы координатного базиса в прямоугольной декартовой системе координат.

Кратко можно записать . Здесь   знак набла.

Пример 3.22. Найти градиент функции в точке .

.

.

Теорема 3.5. Производная функции по направлению вектора равняется проекции градиента этой функции на это направление, т. е.

.

Известно, что проекция некоторого вектора на направление вектора равняется

.

Здесь   угол между векторами и ,  скалярное произведение векторов,  единичный вектор, совпадающий по направлению с вектором .

Найдем

.

Свойство 1. Производная функции по направлению вектора достигает своего наибольшего значения, если направление вектора совпадает с направлением градиента этой функции.

Действительно, производную данной функции по направлению вектора можно записать следующим образом , где   угол между градиентом и вектором . Если этот угол равен нулю  = 0 , то косинус этого угла и производная функции принимают наибольшие значения, cos0 = 1, .

Свойство 2. Производная функции по направлению вектора равняется нулю, если направление вектора перпендикулярно направлению градиента этой функции.

Действительно, .

Данные свойства используются при решении задач оптимизации (нахождения наибольшего, наименьшего значений функций) с помощью численных методов. Градиент функции определяет направление наибольшего изменения функции. Направление перпендикулярное градиенту определяет направление, в котором функция не изменяется.

Известно, что на поверхности уровня функция не изменяется. Следовательно, градиент функции перпендикулярен поверхности уровня. Это обстоятельство можно использовать для написания уравнения касательной плоскости к поверхности . Пусть точка принадлежит поверхности. Найдем градиент функции в этой точке и напишем уравнение плоскости, проходящей через точку перпендикулярно вектору . Получаем уравнение касательной плоскости

.

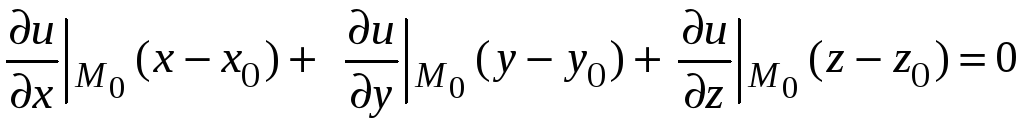Пример 3.23. Написать уравнение касательной плоскости к эллипсоиду

в точке .

Находим ,, ; , , .

Записываем уравнение касательной плоскости

 .