3.9. Достаточные условия дифференцируемости функции нескольких переменных
Теорема 3.4.
Для того, чтобы функция
была дифференцируемой в точке М
(x,
y),
она должна быть непрерывной и иметь
непрерывные частные производные в этой
точке.
Д о к а з а т е л ь
с т в о. Запишем полное приращение функции
.
В правой части
прибавим и вычтем
,
получим
.
По теореме Лагранжа о конечном приращении
,
где
,
,
где
.
Тогда
.
Так как частные производные по условию теоремы непрерывны, то
,
.
Используя теорему 1.3 о представлении функции в виде суммы предела и бесконечно малой функции, запишем
,
,
где
бесконечно малые функции при
.
Учитывая эти выражения, получим
или
.
В соответствии с
определением дифференцируемости функции
это означает, что функция
является дифференцируемой.
Следствие. Для того, чтобы установить дифференцируемость функции, нужно проверить непрерывность частных производных.
3.10. Полный дифференциал функции нескольких переменных
Сумма первых двух слагаемых в выражении полного приращения z называется полным дифференциалом и записывается
.
В частном случае,
если функция z
= x,
то
,
т. е.
.
Аналогично при z
= y,
,
т. е.
.
Учитывая это, полный дифференциал запишем в виде
или
.
Следовательно,
полное приращение функции
равняется сумме полного дифференциала
и бесконечно малой величины более
высокого порядка малости по сравнению
с
.
Найдем
,
т. е. полный дифференциал функции отличается от полного приращения на бесконечно малую функцию более высокого порядка малости по сравнению с x, y. Поэтому полный дифференциал называют главной линейной частью полного приращения функции.
Определение полного дифференциала функции нескольких переменных. Полным дифференциалом функции нескольких переменных называется бесконечно малая функция прямо пропорциональная бесконечно малым приращениям независимых переменных и отличающаяся от полного приращения функции на бесконечно малую функцию более высокого порядка малости по сравнению бесконечно малыми приращениями независимых переменных.
Пример 3.12. Записать полные дифференциалы функций:
1)
;
2)
.
Записываем:
1)
;
2)
.
3.10. 1. Применение полного дифференциала функции нескольких переменных для приближенных вычислений
1. Вычисление значений функций и их приращений.
Используем то, что
полный дифференциал является главной
линейной частью приращения функции
(
).
Пусть известно значение функции
в некоторой точке
и имеется точка
,
находящейся в некоторой достаточно
малой окрестности точки
.
Можно найти
приращение функции
по формуле
.
Можно найти также
значение этой функции в точке
по формуле
.
Здесь
,
приращения независимых переменных,
значения частных
производных функции в точке
.
Пример 3.13. Используя дифференциал, найти приближенно изменение объема цилиндра, если радиус его основания увеличивается от r = 2 м до
r
= 2,1 м., а высота уменьшается от
м
до
м.
Используем формулу
.
Находим
.
.
,
.
V
= 40·0,1+4·(0,5)
= 4
-2
= 2
.
2. Оценка погрешности вычислений значений функций.
Пусть функция
зависит от n
переменных
.
Тогда
.
Абсолютная предельная погрешность функции оценивается по соотношению
или
.
Пример 3.14.
Оценить погрешность вычисления значения
функции
,
если x,
y,
z
примерно равны
,
а их измерения произведены с погрешностью,
не превосходящей 0,1, т. е.
;
.
Находим
;
.
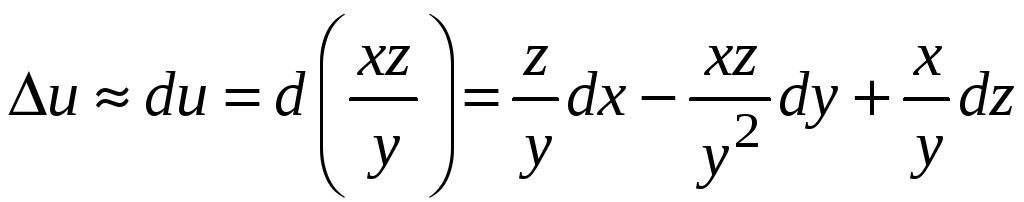Подставляем числовые значения, получаем
.