2.3.4. Теорема Лагранжа о конечном приращении функции
Теорема
Лагранжа.
Если функция
непрерывна на отрезке
и дифференцируемая в каждой его внутренней
точке, то на интервале (a,
b)
найдется такая точка х
= с,
что
.
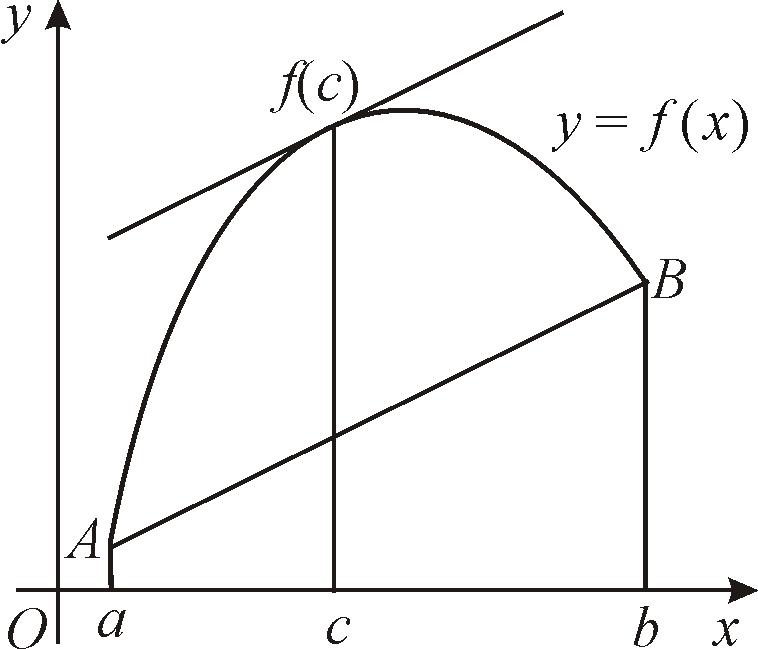
Д о к а з а т е л ь с т в о. Составим вспомогательную функцию y = F(x), которая будет удовлетворять условиям теоремы Ролля.
.
Здесь
уравнение хорды, стягивающей граничные
точки A(a,
f(a))
и B(b,
f(b))
графика функции
(рис. 27); k
– угловой коэффициент этой хорды. На
рисунке для любого значения х
ордината
равняется разности ординаты
и ординаты касательной
(
).
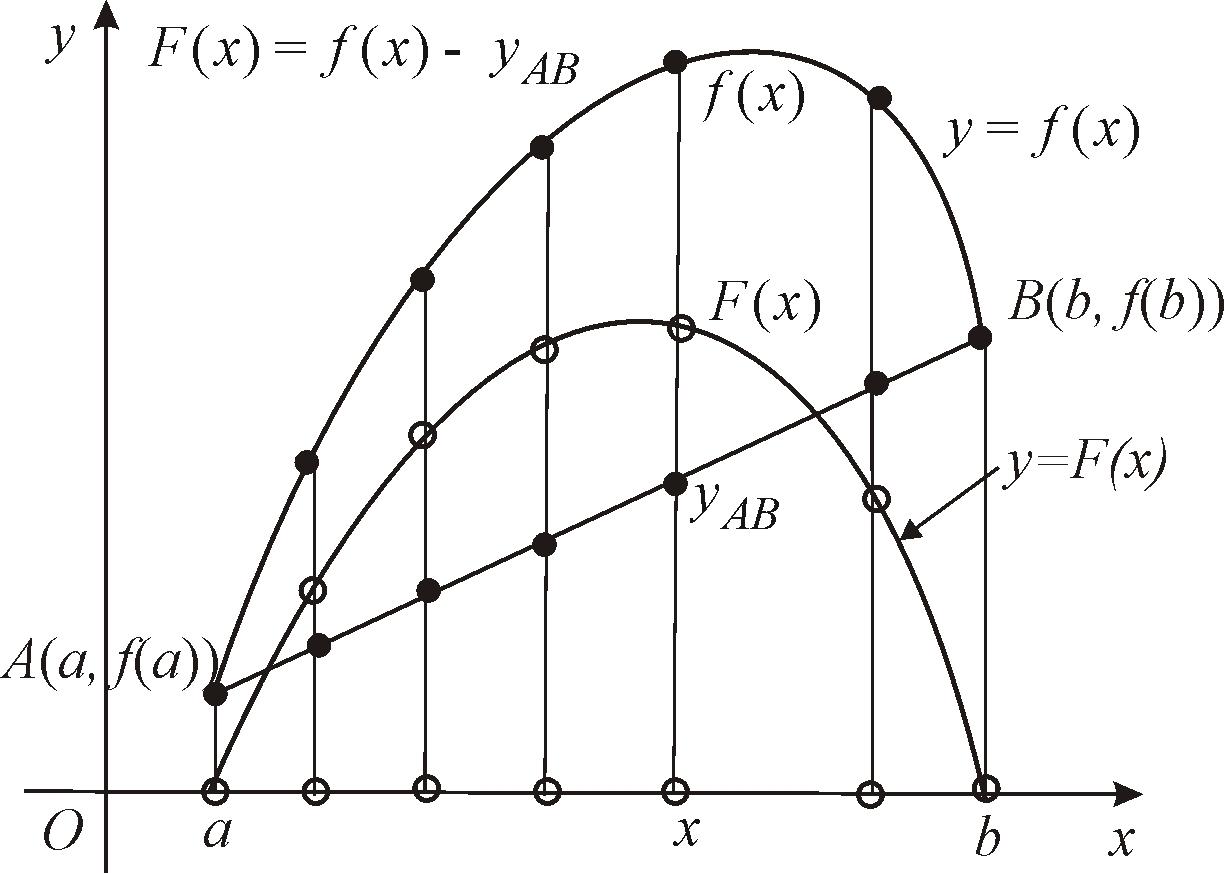
Рис. 27
Очевидно, что
функция y
= F(x)
является непрерывной на отрезке
и дифференцируемая в каждой его внутренней
точке, так как образована с помощью
функций
и y
= x
– a,
удовлетворяющих этим условиям.
Покажем, что
функция y
= F(x)
принимает равные значения в граничных
точках отрезка
.
Действительно,
;
.
Следовательно,
функция y
= F(x)
удовлетворяет всем условиям теоремы
Ролля и поэтому найдется такая внутренняя
точка отрезка
х
= с,
в которой производная этой функции
равна нулю. Найдем производную функции
.
Значение производной функции в точке х = с равно
.
Отсюда получаем
.
Часто рассматривают
функцию y
= f(x)
на отрезке
.
В этом случае последняя формула имеет
вид
.
2.3.5. Геометрический смысл теоремы Лагранжа
На основании
формулы
можно утверждать следующее.
|
Рис. 28 |
Если график
функции y
= f(x)
непрерывный на отрезке
|
и гладкий на интервале
,
то на этом интервале найдется такая
точка
,
в которой касательная параллельна
хорде, стягивающей граничные точки
графика функции (рис. 28).
2.3.6. Теорема Коши
Теорема
Коши. Если
функции y
= f(x)
и y
= g(x)
непрерывные на отрезке
,
дифференцируемые в каждой внутренней
точке этого отрезка и при этом производная
y
= g(x)
ни в одной из этих точек не обращается
в нуль (
),
то найдется такая внутренняя точка
,
что
.
Д о к а з а т е л ь
с т в о. Очевидно, что
,
иначе по теореме Ролля существовала бы
такая точка
,
в которой
,
что противоречит условию теоремы.
Составим вспомогательную функцию y = F(x), которая будет удовлетворять условиям теоремы Ролля.
.
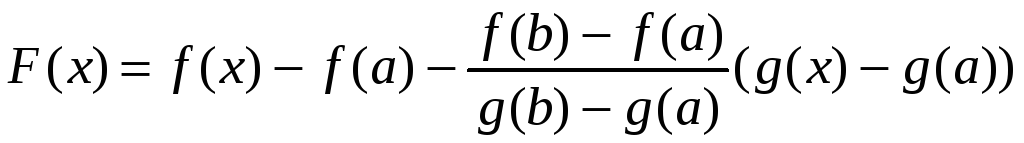Значения функции y = F(x) в точках х = а и х = b равны нулю. Действительно,
,
.
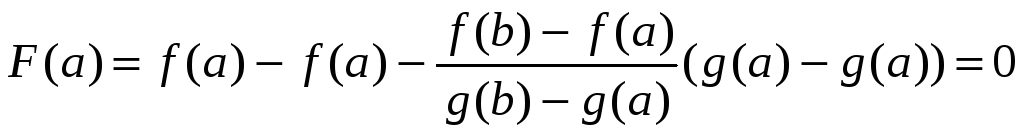Функция y = F(x) является дифференцируемой, так как является линейной комбинацией дифференцируемых функций y = f(x) и y = g(x). Находим
.
По теореме Ролля
существует точка
,
в которой производная функции y
= F(x)
равняется нулю
.
Отсюда получаем
.
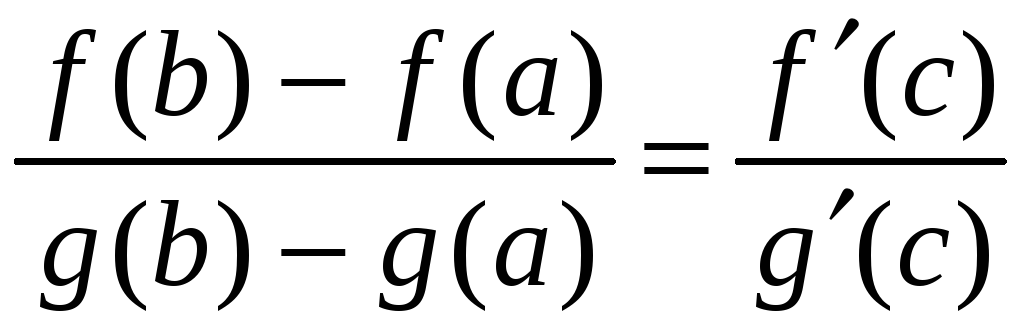2.3.7. Раскрытие неопределенностей при нахождении пределов. Правило Лопиталя
Теорема
2.1. Если в
некоторой окрестности точки
функции y
= f(x)
и y
= g(x)
определены и дифференцируемые, причем
,
пределы функций при
равны нулю, т. е.
,
то предел отношения этих функций
равняется пределу отношения их производных
,
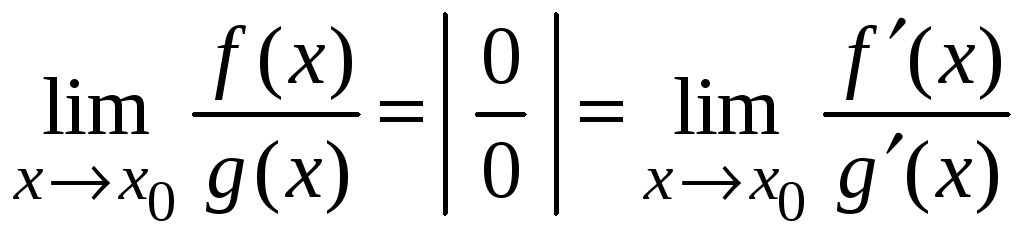если этот предел существует (конечный или бесконечный).
Д о к а з т е л ь с
т в о. Доопределим функции y
= f(x)
и y
= g(x)
так, что
.
Тогда на отрезке
выполняются условия теоремы Коши, т. е.
существует такая точка
,
что
.
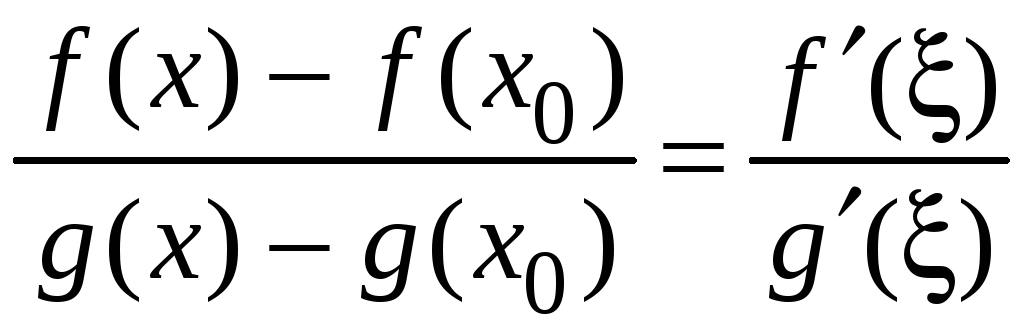Учитывая, что
,
имеем
.
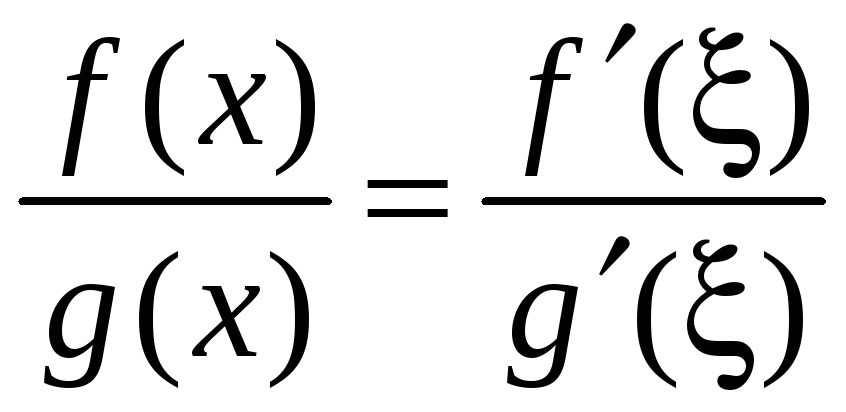Так как при
также и
,
то
.
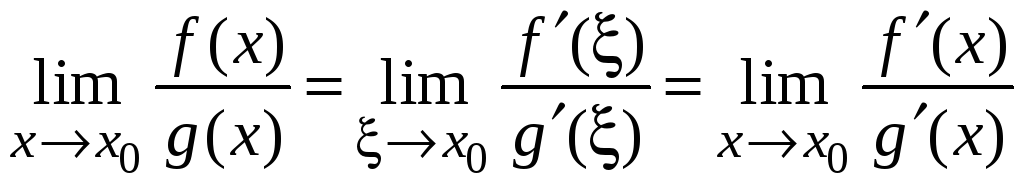Если в результате
применения правила Лопиталя получается
снова неопределенность типа
и производные
и
также удовлетворяют требованиям теоремы,
как функции
и
,
то можно повторно применить правило
Лопиталя, т. е.
.
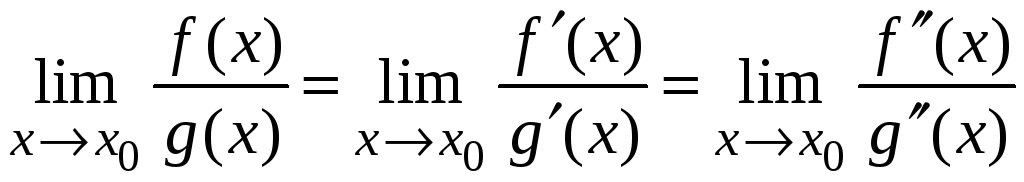Правило
Лопиталя справедливо также в случае
когда
.
Покажем это. Пусть
.
Сделаем замену переменной x
= 1/t.
Тогда при
и
,
.
Применим к функциям
и
правило
Лопиталя, получим
.
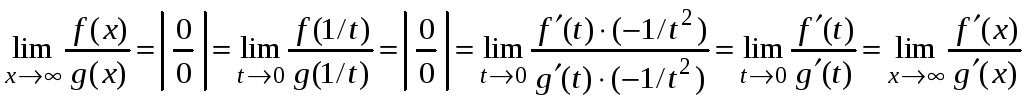Здесь производные
от функций
и
находились по правилу нахождения
производных сложных функций.
Правило Лопиталя
справедливо так же, если
,
т. е имеет место неопределенность типа
,
.
Покажем это.
Преобразуем данный предел к пределу с
неопределенностью типа
и применим правило Лопиталя для этого
случая, получим
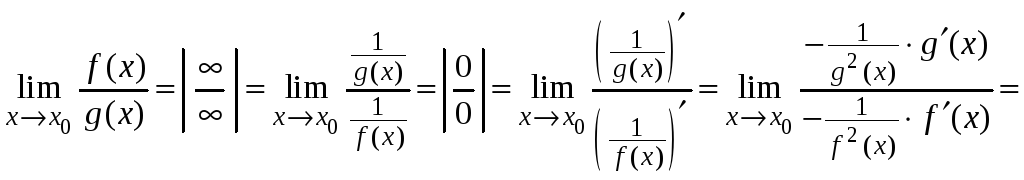
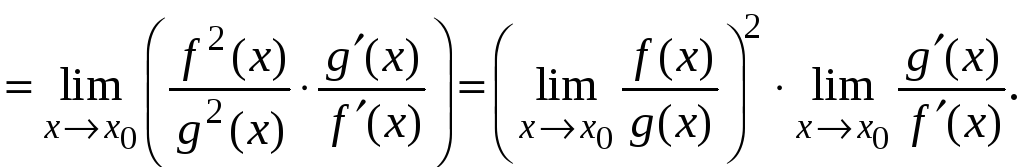
Имеем равенство
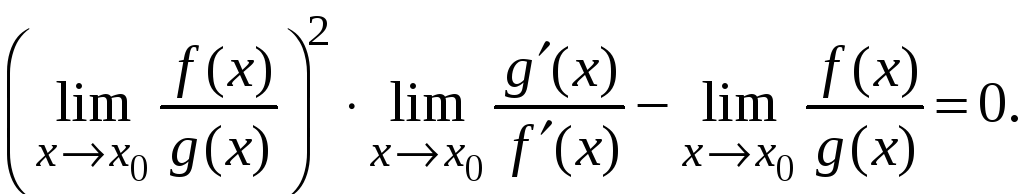Отсюда получаем
,
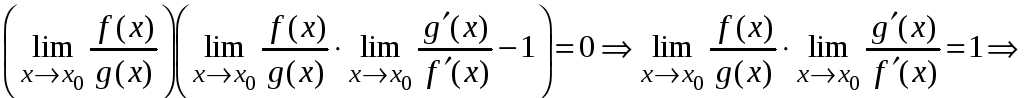
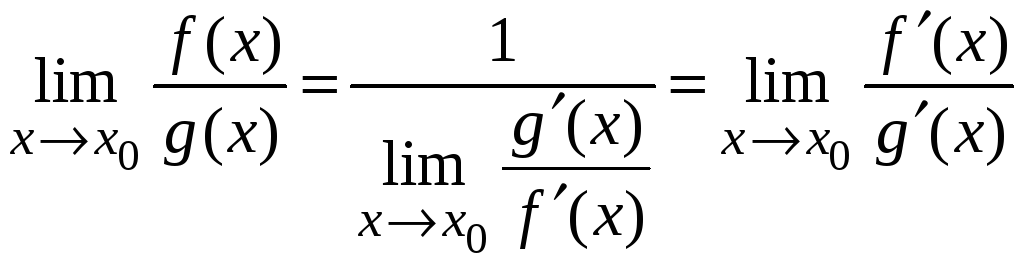т. е.
.
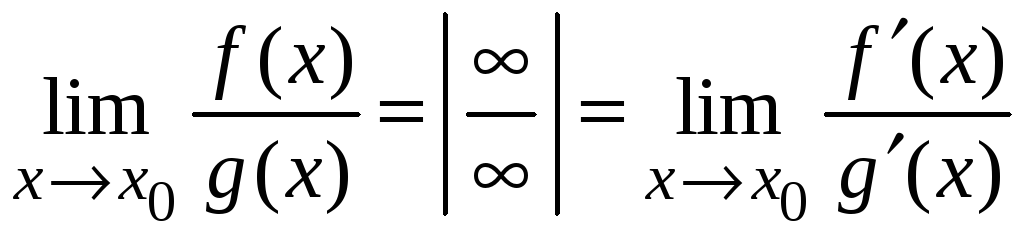Пример
2.10.
.
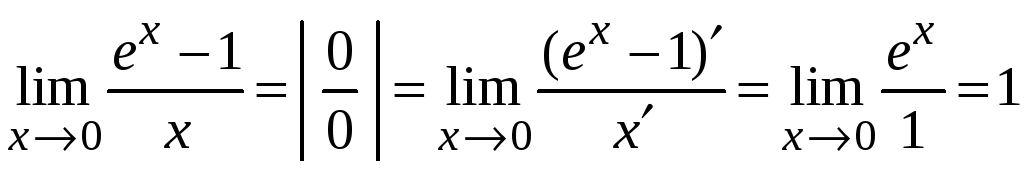Пример
2.11.
.
Пример
2.12.
.
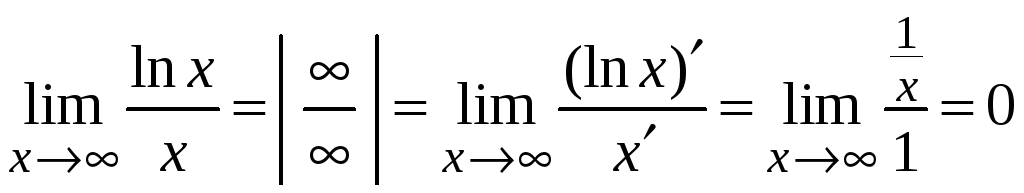Если при нахождении
пределов неопределенность имеет вид
произведения
,
то прежде, чем применять правило
Лопиталя, ее нужно привести к
неопределенностям типа частного
или
.
Пример
2.13.
.
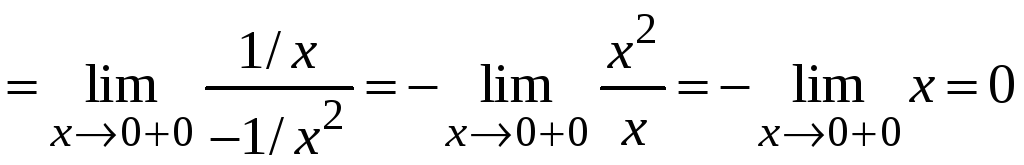Пример
2.14.
.
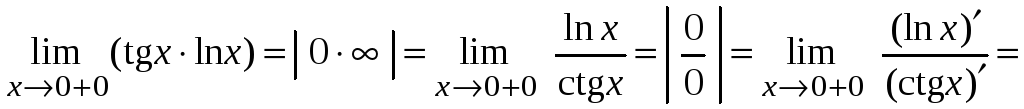
Если при применении правила Лопиталя под пределом имеются некоторые функции, которые не приводят к неопределенности, то эти функции нужно выделить в отдельный предел, т. е. разбить предел на два предела.
Пример 2.15.
.
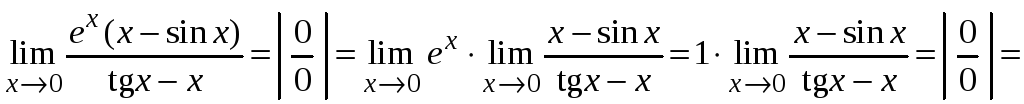
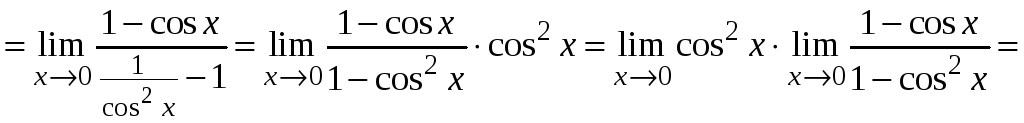
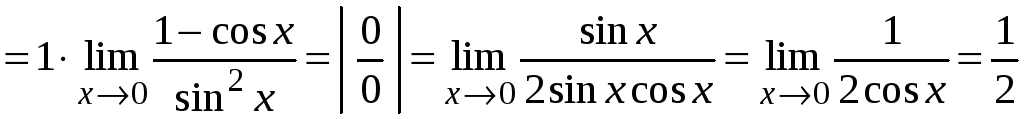