- •Глава II. Дифференциальное исчисление функций одной переменной
- •2.1. Производная функции
- •2.1.1. Определение производной функции
- •2.1.2. Дифференцируемость функции, ее взаимосвязь с производной и непрерывностью функции
- •2.1.3. Непосредственное нахождение производной
- •2.1.4. Геометрический смысл производной
- •2.1.5. Механический смысл производной
- •2.1.6. Правила дифференцирования функций
- •2.1.7. Вывод производных основных элементарных функций
- •2.1.8. Сводка формул Правила дифференцирования
- •2.1.9. Производные высших порядков
- •2.1.10. Эластичность функции
- •2.1.11. Геометрический смысл эластичности
- •2.1.12. Экономический смысл эластичности
- •2.1.13. Свойства эластичности функции
- •2.2. Дифференциал функции одной переменной
- •2.2.1. Определение дифференциала функции
- •2.2.2. Геометрический смысл дифференциала
- •2.2.3. Свойства дифференциала
- •2.2.4. Применение дифференциала для приближенных вычислений
- •2.2.5. Дифференциалы высших порядков
- •2.3. Теоремы о дифференцируемых функциях
- •2.3.1. Теорема Ролля
- •2.3.2. Геометрический смысл теоремы Ролля
- •2.3.3. Примеры использования теоремы Ролля
- •2.3.4. Теорема Лагранжа о конечном приращении функции
- •2.3.5. Геометрический смысл теоремы Лагранжа
- •2.3.6. Теорема Коши
- •2.3.7. Раскрытие неопределенностей при нахождении пределов. Правило Лопиталя
- •2.3.8. Применение правила Лопиталя для раскрытия неопределенностей типа степени
- •2.4. Формулы Тейлора и Маклорена
- •2.4.1. Формула Тейлора. Остаточный член в форме Лагранжа
- •2.4.2. Формула Маклорена
- •2.4.3. Разложение основных элементарных функций по формуле Маклорена
- •2.4.4. Применение формулы Маклорена для вычисления пределов и значений функций
- •2.5. Исследование функций
- •2.5.1. Необходимый и достаточный признаки монотонности функций
- •2.5.2. Определение экстремума функции
- •2.5.3. Необходимый признак экстремума функции
- •2.5.4. Первый достаточный признак экстремума функции (с использованием первой производной)
- •2.5.5. Второй достаточный признак экстремума функции (с использованием производной второго порядка)
- •2.5.6. Определение выпуклости, вогнутости графика функции, точки перегиба
- •2.5.7. Достаточный признак выпуклости, вогнутости графика функции
- •2.5.8. Необходимый признак существования точки перегиба
- •2.5.9. Достаточный признак существования точки перегиба
- •2.5.10. Асимптоты графика функции
- •2.5.11. Построение графика функции
2.1.9. Производные высших порядков
Производной n-го порядка называется производная от производной
(n1)- го порядка.
Для того, чтобы
найти производную n-го
порядка
![]() функции
функции
![]() ,
необходимо найти несколько производных
(первого, второго, третьего порядка и
т. д.), уяснить закономерность их
образования в зависимости от порядка
n
и записать
,
необходимо найти несколько производных
(первого, второго, третьего порядка и
т. д.), уяснить закономерность их
образования в зависимости от порядка
n
и записать
![]() .
.
Пример
2.2. Найти
производные n-го
порядка для функций:
![]() ,
,
![]() и
и
![]() .
.
1.
![]() .
.
2.
![]() ,
,
![]() ,
,
![]()
![]() ,
…,
,
…,
![]() .
.
3.
![]() ,
,
![]() ,
,
![]() ,
,
![]() =
=
![]() =
=
=
 .
.
При нахождении
производной
![]() n-го
порядка функции
n-го
порядка функции
![]() ,
заданной параметрически, т.е.
,
заданной параметрически, т.е.
![]()
необходимо, чтобы
функция
![]() имела обратную функцию
имела обратную функцию
![]() .
.
Ранее была получена формула для нахождения производной первого порядка функции данного вида
 или
или
 .
.
Найдем производную
![]() второго порядка.
второго порядка.
 .
.
Используем формулу производной частного, получаем

или
 .
.
Аналогично можно получить производные более высокого порядка.
Пример 2.3.
Найти производную второго порядка
функции
![]() ,
заданной параметрически,
,
заданной параметрически,
![]()
Данная система представляет параметрическую запись уравнения кривой, называемой циклоидой.
Находим
![]() ,
,
 .
.
2.1.10. Эластичность функции
Определение.
Эластичностью функции
![]() называется предел отношения относительного
приращения функции
называется предел отношения относительного
приращения функции
![]() к относительному приращению независимой
переменной
к относительному приращению независимой
переменной
![]() при
при
![]() ,
т. е.
,
т. е.
 .
.
Ввиду того, что
 эластичность
эластичность
 можно записать в виде
можно записать в виде
![]() .
.
Если обозначить
темп роста функции через
 ,
то
,
то
![]() .
.
Функция называется
эластичной, если
![]() ,
неэластичной, если
,
неэластичной, если
![]() и нейтральной, если
и нейтральной, если
![]() .
.
2.1.11. Геометрический смысл эластичности
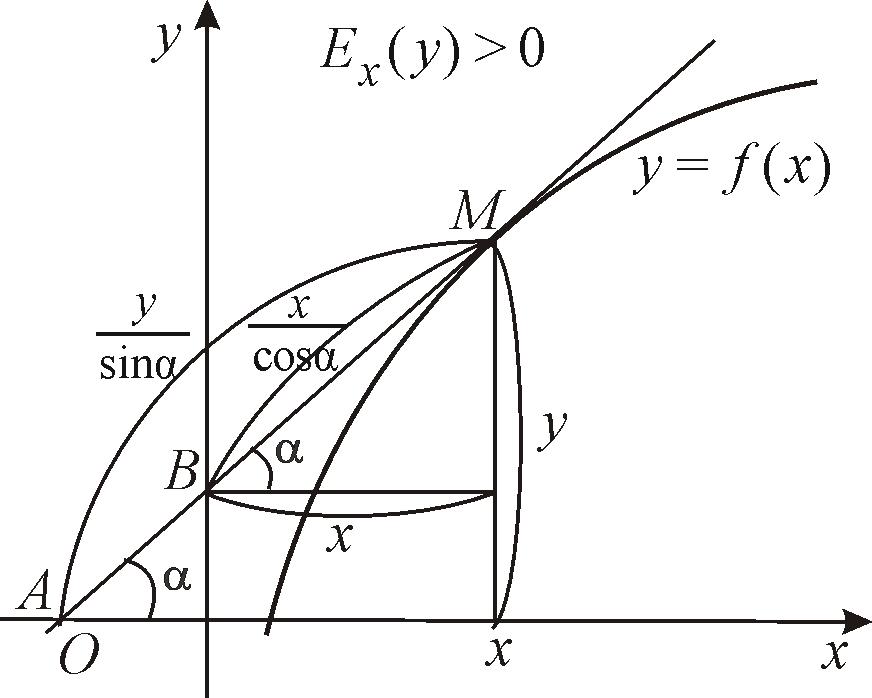
Ввиду того, что производная функции равняется тангенсу угла наклона касательной, формулу для вычисления эластичности можно преобразовать.
 ,
,
где АМ и ВМ – расстояния по касательной от точки касания до пересечения с осями координат Ох и Оy соответственно (рис. 19, рис. 20).
Эластичность
функции
![]() в точке
M
(x,
y)
равна
отношению
расстояний по касательной от этой точки
до осей координат Оy
и Оx
соответственно.
в точке
M
(x,
y)
равна
отношению
расстояний по касательной от этой точки
до осей координат Оy
и Оx
соответственно.
Если точки пересечения касательной в точке M (x, y) с осями координат лежат по одну сторону от этой точки, то эластичность функции в этой точке является положительной величиной. Если же точки пересечения касательной в точке M (x, y) с осями координат лежат по разные стороны от этой точки, то эластичность функции в этой точке является отрицательной величиной.
|
Рис. 19 |
Рис. 20 |
2.1.12. Экономический смысл эластичности
Приближенно можно записать
 .
.
Если
![]() ,
то
,
то
![]() .
.
Эластичность определяет процент относительного изменения функции при изменении относительной величины независимой переменной на 1%.
2.1.13. Свойства эластичности функции
Пусть u = u(x) и v = v(x) – дифференцируемые функции. Получим формулы для эластичности суммы, произведения, частного и обратной функции.
1.  .
.
2.
![]() .
.
3.
 .
.
4.
 .
.
Пример
2.4. Найти
эластичность спроса D
(объема продаж) от цены p,
если: 1)
![]() ;
2)
;
2)
![]() .
.
1.
![]() .
.
 .
.
![]() .
.
Это значит, что спрос нейтрален к предложению. Если цена возрастает на 1%, то спрос уменьшается на 1%. Если же цена уменьшается на 1%, то спрос возрастает на 1%.
2.
![]() .
.
 .
.
![]() .
Это значит, что спрос эластичен. Если
цена возрастает (убывает) на 1%, то объем
продаж уменьшается (возрастает) на 2%.
.
Это значит, что спрос эластичен. Если
цена возрастает (убывает) на 1%, то объем
продаж уменьшается (возрастает) на 2%.
Пример
2.5. Найти
значения цены p,
при которых спрос будет эластичен, если
![]() ,
,
![]() ,
k
– известные постоянные.
,
k
– известные постоянные.
 .
.
Спрос будет
эластичен, если
![]() ,
т. е. если цена p
будет больше
,
т. е. если цена p
будет больше
![]() .
.
Пример 2.6. Найти изменение выручки I(p) с увеличением цены p на товар при различной эластичности спроса.
Выручка равняется произведению объема продаж D(p) на цену товара p, т. е. I(p) = D(p) p. Найдем производную
![]() .
.
Если
![]() ,
то
,
то
![]() и выручка убывает.
и выручка убывает.
Если
![]() ,
то
,
то
![]() и выручка не изменяется.
и выручка не изменяется.
Если
![]() ,
то
,
то
![]() и выручка увеличивается.
и выручка увеличивается.