2.1.7. Вывод производных основных элементарных функций
Получим формулы для нахождения производных основных элементарных функций.
1.
.
При нахождении производной функции
используем определение производной,
формулы преобразования тригонометрических
выражений и первый замечательный предел.
.
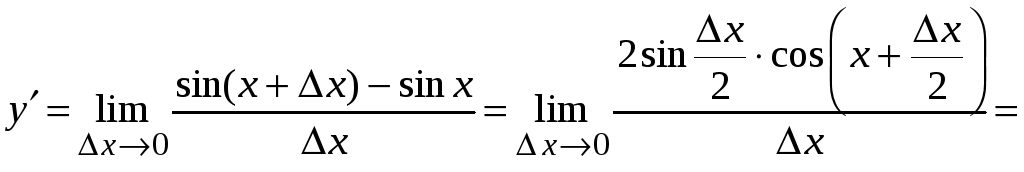
2.
.
Используем формулы приведения и
производную сложной функции, получим
.
3.
.
Используем формулу дифференцирования
частного, получим
.
4.
.
.
При выводе формул нахождения производных обратных тригонометрических функций используем взаимосвязь производных взаимно обратных функций и формулы взаимосвязи тригонометрических функций.
5.
.
Для
обратной функцией является
.
.
6.
.
.
7.
.
.
8.
.
.
9.
.При
нахождении производной логарифмической
функции используем определение
производной и второй замечательный
предел.
.
В частном случае,
когда a
= e,
.
10. При нахождении
производной показательной функции
используем так называемое логарифмическое
дифференцирование. Для этого логарифмируем
равенство
,
получаем
.
Это равенство дифференцируем; при этом
учитываем, что
сложная функция.
.
В частном случае,
когда a
= e
,
.
11. Производную
степенной функции
найдем так же, используя логарифмическое
дифференцирование.
.
В практических
задачах часто встречаются производные
от функций
и
,
которые полезно помнить.
.
.
12. Производная
обобщенно-показательной
(показательно-степенной) функции
.
Используем определение логарифма,
представим функцию в виде
Эту функцию дифференцируем как сложную
показательную функцию.
=
=
.
Как можно заметить производная обобщенно-показательной функции равняется сумме производных как показательной и как степенной функций.
Например: 1)
;
2)
.
13. Производная функции, заданной неявно.
Функция
называется заданной неявно, если она
задана уравнением
,
не разрешенным относительно y.
Чтобы найти производную функции
,
заданную неявно, необходимо каждое
слагаемое уравнения
продифференцировать по x,
учитывая, что y
зависит от x,
и из получившегося уравнения найти
.
Пример
2.1. Найти
производные функций
,
заданных неявно.
1)
.
Находим
.
2)
.
Получаем
.
14. Производная функции, заданной параметрически.
Функция называется заданной параметрически, если функция y и аргумент x заданы в виде функций, зависящих от некоторого параметра t, т. е.
Найдем производную данной функции в общем случае
.
Здесь предполагается,
что функция
имеет обратную функцию
.
Например, пусть функция в параметрической записи имеет вид
Исключим в этой системе параметр t. Получим
,
,
т. е. данная функция представляет окружность в параметрической записи.
Найдем производную данной функции.
.
2.1.8. Сводка формул Правила дифференцирования
1.
.
2.
.
3.
.
4.
.
5.
.
Таблица производных
1.
.
2.
.
2а.
.
2б.
.
2в.
.
3.
.
4.
.
5.
.
6.
.
7.
.
8.
.
9.
.
10.
.
11.
.
12.
.
13.
.
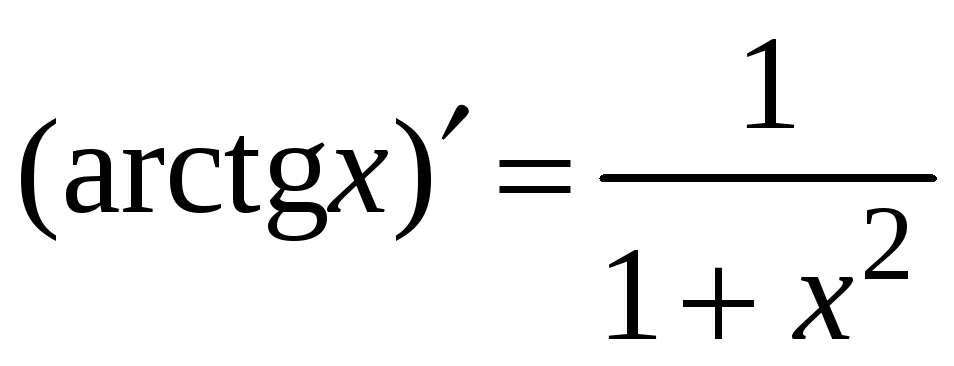14.
.
15.
.
16.
.
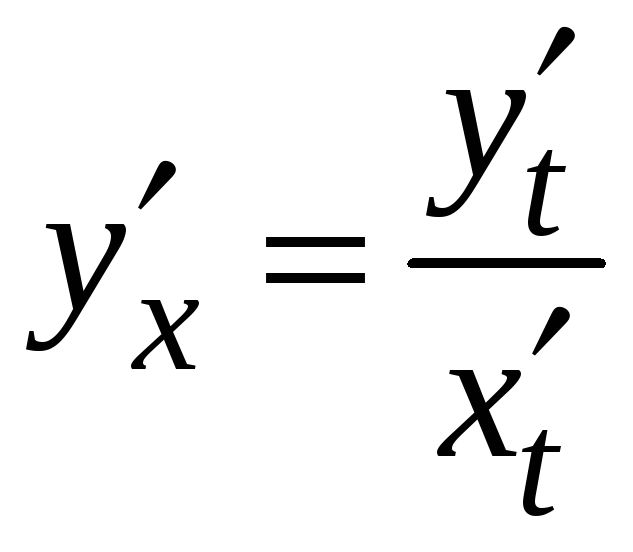