Литература

1. Иродов И.Е. Механика. Основные законы.– М.: Лаборатория базовых знаний, 2003, §§5.4, 6.1, 6.2, 6.3, 6.4.

2. Савельев И.В. Курс общей физики. Механика– М.: АстрельАСТ, 2005; §§5.3, 5.4, 8.1, 8.5, 8.6, 8.7, 8.9, 8.11.

3. Фихтенгольц Г.М. Основы математического анализа. Т.2 ,Москва.: Лань, 2004; Глава 24, 2.

Приложение

При малых углах отклонения маятников от вертикали (, , рис. 2б) ось пружины при колебаниях остается практически горизонтальной (рис.П.1.). В этом случае суммарный момент сил тяжести и упругости относительно оси вращения 1-го маятника равен

где - проекция силы на ось , - деформация пружины. Момент сил, действующих на второй маятник, относительно его оси вращения равен

где , . При малых углах отклонения маятников от вертикали , , поэтому

, .

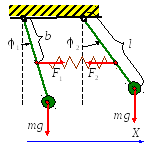
Рис. П.1. Связанные маятники

Полученные выражения для моментов сил подставим в уравнения динамики вращательного движения маятников:

, ,

где - момент инерции каждого маятника относительно оси вращения. После сокращения получим

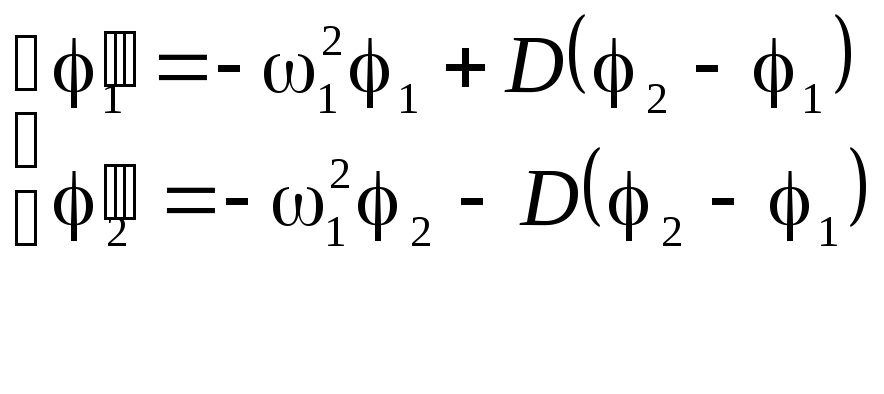, (П1)

где введены обозначения: , . Заметим, что величина равна собственной частоте уединенного (несвязанного) маятника, а величина зависит от параметров маятника и пружины, ее называют коэффициентом связи системы.