3. Логарифмическая функция .
Графики логарифмических функций, соответствующие различным основаниям логарифма представлены на рисунке 18.
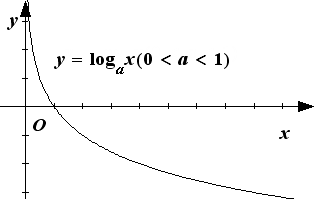
Рис. 18.
4. Тригонометрические функции: y=sin x, y=cos x, y=tg x, y=ctg x; их графики представлены на рисунках 19-а, 19-б.
Рис.19-а
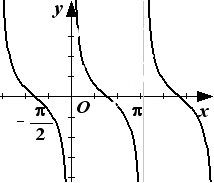
y=ctg x y=tgx
Рис. 19-б.
5. Обратные тригонометрические функции: y=arcsinx, y=arccosx, y=arctgx, y=arcctgx. На рисунке 20 изображены графики обратных тригонометрических функций.
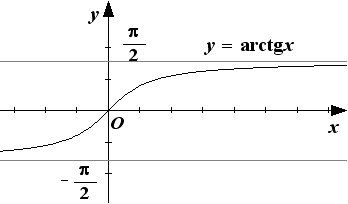
Рис. 20.
Функция называется элементарной, если она задана аналитически одной формулой у=f(x), составленной из основных элементарных функций при помощи конечного числа арифметических действий (сложения, вычитания, умножения и деления) и конечного числа операций образования сложной функции.
Примеры элементарных функций:
;
;
.
Примерами неэлементарных функций могут служить функции:
у =
;
.
Классификация функций.
Элементарные функции делятся на алгебраические и неалгебраические (трансцендентные).
Алгебраической называется функция, в которой над аргументом проводится конечное число алгебраических действий. К числу алгебраических функций относятся:
-
целая рациональная функция (многочлен или полином):
;
-
дробно-рациональная функция – отношение двух полиномов;
-
иррациональная функция (если в составе операций над аргументом имеется извлечение корня).
Всякая неалгебраическая функция называется трансцендентной. К числу трансцендентных функций относятся функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические.
2.10. Преобразования графиков.
Если известен график функции у=f(x), то с помощью некоторых преобразований (параллельного переноса, осевой и центральной симметрии и т.п.) можно построить графики более сложных функций.
-
График функции у=−f(x) получается из графика у=f(x) путем симметрии относительно оси Ох (рис. 21).
Рис. 21
2) График функции у=f(−x) получается из графика у=f(x) путем симметрии относительно оси Оу (рис. 22).
Рис. 22
3)
График функции y=kf(x)
получается из графика у=f(x)
путем растяжения в «k»
раз вдоль Оу, при k>1,
а при 0<k<1 − путем
сжатия в «
»
раз вдоль Оу На рисунке 23 преобразования
такого рода рассмотрены на примере
растяжения и сжатия синусоиды в 3 и 2
раза соответственно.
4)
График функции y=f(kx)
получается сжатием графика у=f(x)
в «k» раз вдоль Ох,
при k>1, а при 0<k<1
– растяжением графика у=f(x)
в «
»
раз вдоль Ох. Данные преобразования
продемонстрированы на рисунке 24 на
примере преобразований синусоиды.
Рис. 23.
Рис. 24
5) График функции у=f(x+a) получается из графика у=f(x) параллельным переносом на |а|, при а>0 влево вдоль оси Ох, а при a<0 − вправо вдоль оси Ох (рис. 25).
Рис. 25
6) График функции y=f(x)+a, получается параллельным переносом графика у=f(x) на |а|, при a>0 вверх вдоль оси Оу, а при a<0 − вниз вдоль оси Оу (рис. 26).
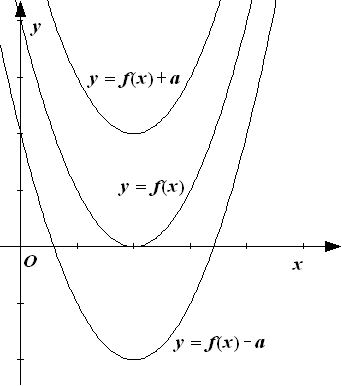
Рис. 26
7) График функции y=|f(x)| получается из графика у=f(x) следующим образом: часть графика у=f(x), лежащая выше оси Ох остается, а лежащая ниже − симметрично отображается вверх относительно оси Ох (На рисунке 27-а изображен график функции у=f(x), а на рисунке 27-б − график функции y=|f(x)|).
8) График функции y=f(|x|) получается из графика у=f(x) путем следующих преобразований: часть графика у=f(x), лежащая правее оси Оу остается и симметрично отображается влево относительно оси Оу, остальная часть графика (лежащая левее оси Оу) отбрасывается. На рисунках 28-а и 28-б изображены графики функций у=f(x) и y=f(|x|) соответственно.
Рис. 27-а Рис. 27-б
Рис. 28-а Рис. 28-б