
- •§2. Функция.
- •2.1. Понятие функции. Способы задания функции.
- •Свойства функции.
- •2.2. Область существования и область значения функции.
- •2.3. Четность и нечетность.
- •2.4. Периодичность.
- •2.5. Монотонность.
- •2.6. Ограниченность.
- •2.7. Обратная функция и ее график.
- •2.8. Сложная функция.
- •2.9. Элементарные функции. Классификация функций.
- •3. Логарифмическая функция .
- •2.10. Преобразования графиков.
2.6. Ограниченность.
Определение. Функция y=f(x) называется ограниченной на некотором промежутке Х, если существует такое положительное число М>0, что
|f(x)| £ М для любого хÎХ,
Краткая
запись: ($М >0)
("хÎХ)
[|f(x)|![]() M]
.
M]
.
Или
($а, bÎR) ("хÎХ) [а£f(x)£ b]
В противном случае функция называется неограниченной.
Если функция ограничена на некотором промежутке, то график ее в пределах этого интервала расположен в полосе, ограниченной прямыми у=а и у=b (рис. 13).

Пример. Функция у= sin x ограничена на всей числовой оси, т.к.
("хÎR) [|sin x|£1 ].
2.7. Обратная функция и ее график.
Пусть у=f(х)
есть функция от независимой переменной
х, определенной на множестве Х
с областью значений У. Поставим в
соответствие каждому уÎУ
единственное значение хÎХ,
при котором f(х)=у.
Тогда полученная функция х=![]() (у)=f
(у)=f![]() (y),
определенная на множестве У с
областью значений Х, называется
обратной.
(y),
определенная на множестве У с
областью значений Х, называется
обратной.
Чтобы найти функцию х=![]() (у),
обратную к функции у=f(x),
достаточно решить уравнение f(x)=y
относительно х (если это возможно).
(у),
обратную к функции у=f(x),
достаточно решить уравнение f(x)=y
относительно х (если это возможно).
Если сохранить обычные обозначения,
т.е. если во всех случаях х считать
аргументом и у – функцией, то получим,
что функция у=![]() (х)
является обратной по отношению к функции
у=f(х).
(х)
является обратной по отношению к функции
у=f(х).
График обратной функции у=![]() (х)
симметричен относительно прямой у=х.
(х)
симметричен относительно прямой у=х.
Примеры взаимообратных функций:
-
у = а
 и у = log
и у = log х;
х;
-
у = 2х и у=
 ;
;
3) Для
функции у=х![]() ,
х Î [0;1], обратной
является х=
,
х Î [0;1], обратной
является х=![]() ;
заметим, что для функции у=х
;
заметим, что для функции у=х![]() ,заданной
на отрезке [−1;1], обратной не существует,
т.к. одному значению у соответствует
два значения х (так, если у=1, то
х1=1, х2=−1).
,заданной
на отрезке [−1;1], обратной не существует,
т.к. одному значению у соответствует
два значения х (так, если у=1, то
х1=1, х2=−1).
Из определения обратной функции вытекает, что функция у=f(х) имеет обратную, тогда и только тогда, когда функция у=f(х) задает взаимно однозначное соответствие между множествами Х и У. Отсюда следует, что любая строго монотонная функция имеет обратную. При этом, если функция возрастает (убывает), то обратная функция также возрастает (убывает).
2.8. Сложная функция.
Если у является функцией от переменной u, а переменная u в свою очередь является функцией от переменной х, т.е. у=f(u) и u=j(x), то функция у=f[j(x)] называется функцией от функции или сложной функцией (или суперпозицией заданных функций).
Переменная u в этом случае называется промежуточной переменной.
Примеры.
-
Функция у=lg(x
 +5x)
есть сложная функция, т.к. эту функцию
можно представить так: у=lg
u, где u=x
+5x)
есть сложная функция, т.к. эту функцию
можно представить так: у=lg
u, где u=x +5x.
+5x. -
Функция у=sin(2x+1) есть сложная функция; ее можно представить так: у=sin u, где u=2x+1.
Замечание.
Сложная функция может иметь несколько
промежуточных переменных. Например,
сложная функция у=![]() имеет две промежуточные переменные:
у=2t; где
t=cos u;
u=x
имеет две промежуточные переменные:
у=2t; где
t=cos u;
u=x![]() .
.
2.9. Элементарные функции. Классификация функций.
Основными элементарными функциями называют следующие функции:
-
Степенная функция
 ,
n
,
n R.
R.
Примеры графиков степенных функций, соответствующих различным показателям степени представлены ниже.
1)
![]() ,
n
,
n![]() N.
Графики функций, соответствующие
показателям степени n=1,
а также для n – четного
и n – нечетного
представлены на рисунке 14.
N.
Графики функций, соответствующие
показателям степени n=1,
а также для n – четного
и n – нечетного
представлены на рисунке 14.
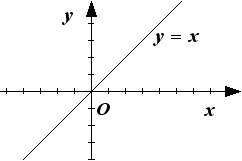


Рис. 14
2)
![]() ,
n
,
n![]() N
(рис. 15).
N
(рис. 15).


Рис. 15.
3)
![]() n
n![]() N,
n>1. Графики таких
функций (два случая в зависимости от
четности n) представлены
на рисунке 16.
N,
n>1. Графики таких
функций (два случая в зависимости от
четности n) представлены
на рисунке 16.


Рис. 16.
2. Показательная функция
![]() .
.
На рисунке 17 показаны графики показательных функций, соответствующие различным основаниям степени.


Рис. 17.
