Лабораторна робота №2

Тема: Побудова та аналіз багаточинникової економетричної моделі.

Мета: Оцінити параметри багаточинникової економетричної моделі методом 1 МНК й дати їм економічне тлумачення.

Короткі теоретичні відомості

Для кількісного опису зв’язку між результативною ознакою і кількома чинниками необхідно побудувати економетричну модель, що базується на регресійному аналізі.

У загальному випадку ця модель має вигляд

, (2.1)

де – вектор змінної, що характеризує результативну ознаку; – вектор незалежних змінних, що характеризують чинники моделі; – стохастична складова. Залежну змінну називають також пояснювальною, ендогенною змінною; незалежні змінні – пояснюючими, екзогенними змінними.

У найпростішому випадку економетрична модель є лінійною, аналітична форма якої записується у вигляді:

, (2.2)

де , – невідомі параметри моделі.

В матричній формі лінійна багаточинникова економетрична модель має вигляд:

Y=XB+e (2.3)

де – вектор ендогенних змінних; – матриця екзогенних змінних; – вектор оцінок параметрів моделі; – вектор залишків.

Параметри моделі (2.2) можна оцінити на основі методу 1 МНК. Але при цьому необхідно дотримуватися таких передумов (гіпотез):

• математичне сподівання залишків дорівнює нулю, тобто

M(e)=0; (2.4)

• значення вектора залишків незалежні між собою і мають постійну дисперсію:

M(e)=E (2.5)

де – транспонований вектор залишків, E – одинична матриця;

• Незалежні змінні моделі не зв’язані з залишками, тобто

M(e)=0; (2.6)

де – транспонована матриця незалежних змінних.

Незалежні змінні створюють лінійно-незалежну систему векторів:

(2.7)

Оператор оцінювання параметрів багаточинникової економетричної моделі на основі 1 МНК дорівнює:

(2.8)

Можна довести, що оцінки B, які можна отримати на основі оператора оцінювання (2.8), мінімізують суму квадратів залишків (). При цьому значення вектора є розв’язком системи нормальних рівнянь:

(2.9)

де – матриця моментів. Числа, що стоять на головній діагоналі матриці, характеризують величину дисперсій незалежних змінних чинників, а інші елементи відповідають взаємним коваріаціям.

Оцінка параметрів багаточинникової економетричної моделі повинна бути незміщеною і виконуватися рівність:

(2.10)

У випадку якщо рівність (2.10) не виконується, знаходять різницю – зміщення оцінки.

Оцінка параметрів моделі повинна бути обґрунтованою, тобто при заданій малій величині справедливе співвідношення:

(2.11)

Елементами оператора оцінювання

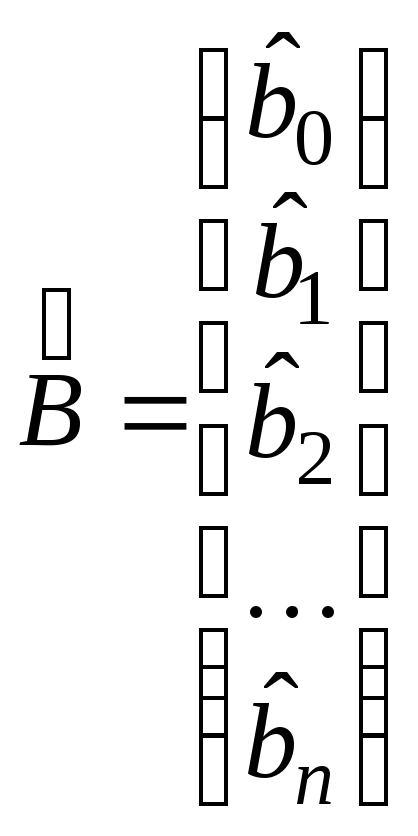(2.12)

є оцінки невідомих параметрів моделі:

x₁+x₂+…+x_i+…x_n (2.13)

Вектор залишків знаходять як різницю векторів:

e, (2.14)

елементи якого визначають за виразом:

(2.15)

Дисперсії залишків і залежної змінної можна в матричній формі розрахувати за виразами:

(2.16)

Матрицю коваріацій оцінок параметрів моделі в матричній формі визначають за виразом:

(2.17)

Діагональні елементи цієї матриці характеризують дисперсії оцінок параметрів моделі:

Всі інші елементи матриці (2.18) визначають рівень коваріації між оцінками параметрів моделі.

Стандартні помилки оцінок параметрів знаходять за виразами:

; , … (2.18)

а їхні відносні відхилення – за виразами:

; … (2.19)

Завдання

Дані, що характеризують урожайність зернових, для шістнадцяти районів області наведені у наступній таблиці 2.1

Таблиця 2.1

№ п/п	Урожайність ц/га	Число тракторів на 104 га угідь	Число зернозбиральних комбайнів на 104 га угідь	Число знарядь обробки ґрунту на 104 га угідь	Кількість добрив на 100 га угідь
1	19,4+	159+	26+	205+	32+
2	16,8+	34+	28+	46+	59+
3	18,0+	253+	31+	246+	30+
4	19,8+	263+	40+	344+	43+
5	19,2+	216+	26+	216+	39+
6	17,2+	216+	30+	269+	32+
7	25,0+	168+	29+	73+	42+
8	15,2+	35+	26+	42+	21+
9	13,8+	52+	24+	49+	20+
10	27,0+	342+	31+	302+	137+
11	19,4+	178+	30+	319+	73+
12	21,4+	240+	32+	330+	25+
13	24,2+	336+	40+	451+	59+
14	19,4+	172+	28+	226+	82+
15	14,0+	59+	29+	60+	13+
16	14,4+	28+	26+	30+	9+

Дослідити залежність між урожайністю зернових та іншими чинниками, що наведені у таблиці 2.1, і провести аналіз побудованої багатофакторної економетричної моделі. Залежність між результуючою ознакою та чинниками вважати лінійною. При проведенні розрахунків використати систему Mathcad. Сформувати базу даних згідно свого варіанту:в таблиці 2.1 за N прийняти дві останні цифрі номера своєї залікової книжки.