
- •Оглавление
- •Введение
- •1. Аналитическая геометрия и линейная алгебра.
- •Занятие № 5. Линейные пространства.
- •Занятие № 6. Евклидовы пространства.
- •Занятие № 7. Линейные операторы и матрицы.
- •Занятие № 10. Скалярное произведение векторов.
- •Занятие № 11. Векторное и смешанное произведение векторов.
- •Занятие № 12. Прямая на плоскости.
- •Занятие № 13. Кривые второго порядка.
- •Занятие № 14. Преобразование координат на плоскости. Приведение уравнений к каноническому виду.
- •Занятие № 15. Плоскость в пространстве.
- •Занятие № 16. Прямая в пространстве.
- •Занятие № 17. Взаимное расположение прямых и плоскостей в пространстве.
- •Занятие № 18. Поверхности в пространстве.
- •2. Введение в математический анализ.
- •21.3. Доказать, что последовательность
- •4. Интегральное исчисление функций одной переменной.
- •5. Дифференциальное исчисление функций нескольких переменных.
- •Занятие № 46. Пределы и непрерывность функции нескольких переменных.
- •Занятие № 47. Частные производные и дифференциалы.
- •Занятие № 48. Касательная плоскость и нормаль к поверхности.
- •Занятие № 49. Производная по направлению. Градиент.
- •6. Интегральное исчисление функций нескольких переменных. Занятие № 53. Двойные интегралы.
- •7. Ряды.
- •8. Обыкновенные дифференциальные уравнения.
- •19.1. A); б); в); г). 19.2. А); б); в); г). 19.3. А) четная; б) общего вида; в) нечетная.
- •27.4. Касательная , нормаль . 27.5.
- •Рекомендуемая литература
Занятие № 46. Пределы и непрерывность функции нескольких переменных.
46.1
Вычислить пределы
![]() ,
,
![]() ,
,
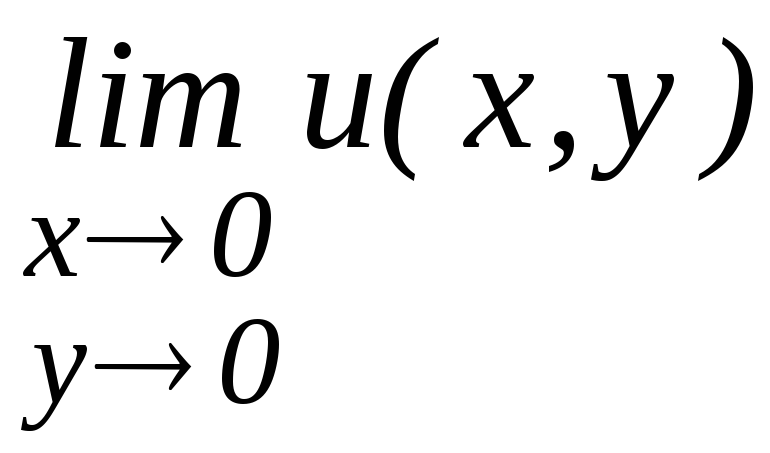 :
:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ; г)
; г)
![]() .
.
46.2.
Вычислить пределы
![]() ,
,
![]() ,
,
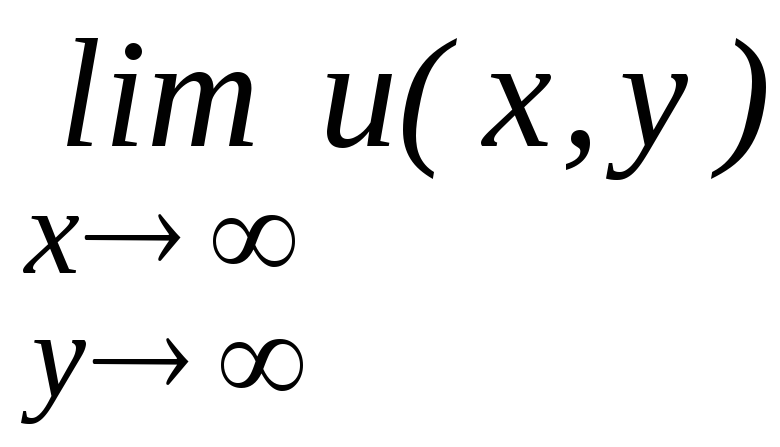 :
:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() .
.
46.3. Исследовать на непрерывность функции в точке (0;0):
а)
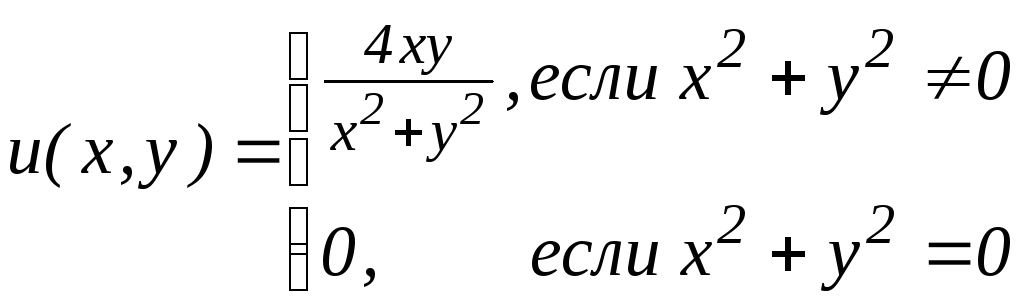 ;
;
б)
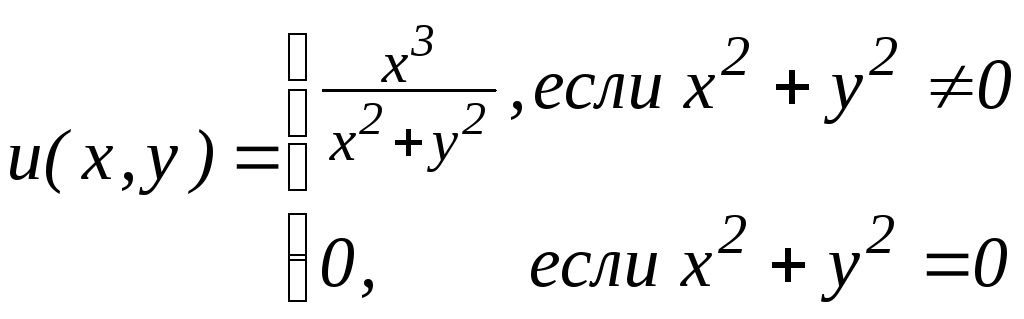 ;
;
в)
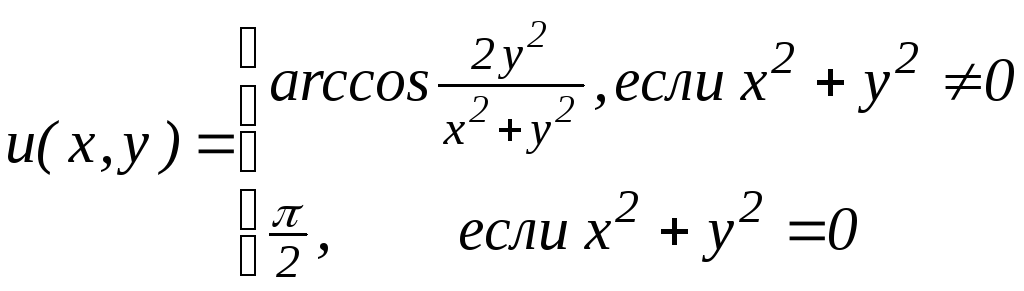
46.4. Найти и исследовать все точки разрыва функций:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
Занятие № 47. Частные производные и дифференциалы.
47.1. Найти частные производные первого порядка следующих функций:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
.
47.2. Найти частные производные первого и второго порядков следующих функций:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() .
.
47.3. Найти дифференциалы первого и второго порядков от следующих функций:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
47.4. Найти производные первого и второго порядков от следующих сложных функций:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
47.5.
Найти дифференциалы первого и второго
порядков от следующих сложных функций:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
Занятие № 48. Касательная плоскость и нормаль к поверхности.
48.1. Написать уравнения касательной плоскости к поверхности:
а)
![]() в точке (1;-2;3);
в точке (1;-2;3);
б)
![]() в точке (2;3;2);
в точке (2;3;2);
в)
![]() в точке (1;1;1);
в точке (1;1;1);
г)
![]() в точке (3;4;1c).
в точке (3;4;1c).
48.2.
Определить плоскость, касательную к
поверхности
![]() и параллельную плоскости
и параллельную плоскости
![]() .
.
48.3.
Написать уравнения нормали в точке (2;
-1; 4) к поверхности конуса
![]() .
.
48.4.
Найти углы с осями координат нормали к
поверхности
![]() в точке (0; 2;-3).
в точке (0; 2;-3).
48.5.
Написать уравнения нормали к поверхности
![]() в точке (2; 5; 1).
в точке (2; 5; 1).
48.6.
Найти углы с осями координат нормали к
поверхности
![]() в точке (3;3; 0)
в точке (3;3; 0)
48.7
В какой точке касательная плоскость к
поверхности
![]() параллельна:
параллельна:
1) плоскости хОу;
2)
плоскости
![]() ;
;
Написать уравнения этих касательных плоскостей.
Занятие № 49. Производная по направлению. Градиент.
49.1
Пусть
![]() .
Построить линии уровней и grad
u
в точке А(3;2).
.
Построить линии уровней и grad
u
в точке А(3;2).
49.2.
Пусть
![]() . Построить линии уровней и grad
u:
. Построить линии уровней и grad
u:
а)
в любой точке прямой
![]() ;
;
б)
в любой точке прямой
![]() .
.
49.3.
Найти градиент функции
![]() в точке А(4;-2;7).
в точке А(4;-2;7).
49.4.
Найти производную функции
![]() в
точке (1;1;1) в направлении вектора
в
точке (1;1;1) в направлении вектора
![]() ,
и найти grad
u
в той же точке и его длину. Построить
поверхности уровней.
,
и найти grad
u
в той же точке и его длину. Построить
поверхности уровней.
49.5.
Найти производную функции
![]() в точке (2;3; 4) в направлении радиус-вектора
этой точки.
в точке (2;3; 4) в направлении радиус-вектора
этой точки.
49.6.
Построить линии уровня функции
![]() , проходящей через точку А(4;4). Построить
grad
u(4;
4)
и убедиться, что он перпендикулярен
линии уровня.
, проходящей через точку А(4;4). Построить
grad
u(4;
4)
и убедиться, что он перпендикулярен
линии уровня.
49.7.
Для функции
![]() построить линии уровня и градиент.
Сравнить их направления в точках (2;2) и
(2;-2).
построить линии уровня и градиент.
Сравнить их направления в точках (2;2) и
(2;-2).
49.8. Найти угол между градиентами функции u в точках А и В, если:
а)
![]() ;
;
б)
![]() .
.
Занятие № 50.
Исследование функций нескольких переменных на экстремум.
50.1. Найти стационарные точки и исследовать на экстремум следующие функции:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() .
.
50.2. Исследовать на экстремум следующие функции нескольких переменных:
а)
![]() :
:
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() .
.
Занятие № 51.
Условный экстремум функций нескольких переменных.
51.1. Методом подстановки найти точки условного экстремума следующих функций:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
ж)
![]() ;
;
з)
![]() .
.
51.2. Методом множителей Лагранжа найти точки условного экстремума следующих функций:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
ж)
![]() ;
;
з)
![]() .
.
Занятие № 52.
Нахождение наибольшего и наименьшего значений функций нескольких переменных.
52.1. Найти наибольшее или наименьшее значения следующих функций на заданном множестве:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() .
52.2. Найти расстояние между кривой
.
52.2. Найти расстояние между кривой
![]() и
прямой
и
прямой
![]() .
.
52.3.
Найти точку, сумма квадратов расстояний
от которой до прямых
![]() наименьшее.
наименьшее.
52.4. Найти наибольший объем прямоугольного параллелепипеда с заданной площадью его поверхности S.
52.5. Определить размеры прямоугольного параллелепипеда данного объема V, имеющего наименьшую площадь поверхности.
52.6. Из всех конусов с данной боковой поверхностью S найти конус с наибольшим объемом.
52.7. В полушар радиуса R вписать прямоугольный параллелепипед наибольшего объема.
