
- •Оглавление
- •Введение
- •1. Аналитическая геометрия и линейная алгебра.
- •Занятие № 5. Линейные пространства.
- •Занятие № 6. Евклидовы пространства.
- •Занятие № 7. Линейные операторы и матрицы.
- •Занятие № 10. Скалярное произведение векторов.
- •Занятие № 11. Векторное и смешанное произведение векторов.
- •Занятие № 12. Прямая на плоскости.
- •Занятие № 13. Кривые второго порядка.
- •Занятие № 14. Преобразование координат на плоскости. Приведение уравнений к каноническому виду.
- •Занятие № 15. Плоскость в пространстве.
- •Занятие № 16. Прямая в пространстве.
- •Занятие № 17. Взаимное расположение прямых и плоскостей в пространстве.
- •Занятие № 18. Поверхности в пространстве.
- •2. Введение в математический анализ.
- •21.3. Доказать, что последовательность
- •4. Интегральное исчисление функций одной переменной.
- •5. Дифференциальное исчисление функций нескольких переменных.
- •Занятие № 46. Пределы и непрерывность функции нескольких переменных.
- •Занятие № 47. Частные производные и дифференциалы.
- •Занятие № 48. Касательная плоскость и нормаль к поверхности.
- •Занятие № 49. Производная по направлению. Градиент.
- •6. Интегральное исчисление функций нескольких переменных. Занятие № 53. Двойные интегралы.
- •7. Ряды.
- •8. Обыкновенные дифференциальные уравнения.
- •19.1. A); б); в); г). 19.2. А); б); в); г). 19.3. А) четная; б) общего вида; в) нечетная.
- •27.4. Касательная , нормаль . 27.5.
- •Рекомендуемая литература
19.1. A); б); в); г). 19.2. А); б); в); г). 19.3. А) четная; б) общего вида; в) нечетная.
19.4.
а)![]() ;
б) непериодическая. 19.5.
;
б) непериодическая. 19.5.
![]() .
22.3.
а) 10; б) 0; в) ∞. 22.4.
а) 5; б) -0,5; в) ∞; г) 0. 22.5.
а) 1; б) 0,5; в) 3/2; г) -2/3; д) 0,5 при
.
22.3.
а) 10; б) 0; в) ∞. 22.4.
а) 5; б) -0,5; в) ∞; г) 0. 22.5.
а) 1; б) 0,5; в) 3/2; г) -2/3; д) 0,5 при
![]() и 0 при
и 0 при
![]() ;
е) ∞ при
;
е) ∞ при
![]() и -1,5 при
и -1,5 при![]() .
22.6.
а)
-1; б) 3; в) 1/9 при
.
22.6.
а)
-1; б) 3; в) 1/9 при
![]() и -4 при
и -4 при
![]() .
22.7.
а) 1; б) 2 . 22.8.
а) 1,875; б) 0,2. 23.1.
а) -6 ; б) -1/3; в) ∞; г) 0,375; д) -4,5 ; е)
.
22.7.
а) 1; б) 2 . 22.8.
а) 1,875; б) 0,2. 23.1.
а) -6 ; б) -1/3; в) ∞; г) 0,375; д) -4,5 ; е)
![]() ;
;
ж)
0 ; з) 6. 23.2.
а) 3; б) 2 ; в)
![]() ;
г) -1/4; д) ∞. 23.3.
а) -1; б)0; в) 1; г) -5; д) ∞ ; е) ∞; ж)
0; з) 2, 5 при
;
г) -1/4; д) ∞. 23.3.
а) -1; б)0; в) 1; г) -5; д) ∞ ; е) ∞; ж)
0; з) 2, 5 при
![]() ∞ при
∞ при
![]() .
24.1.
а) 1; б) 2 ; в) 1,25; г) ∞; д) 0; е) 1; ж) -1/8;
з) 0,7; и) 27; к) 0,25; л) -6; м) 0,5. 24.2.
а) е8
; б) е; в) е-12
; г) 1; д) ∞; е) 1; ж) 0 ; з) 1/12; и) ∞ ; к)
-0,04; л) 0. 25.1.
а) 1; б)
.
24.1.
а) 1; б) 2 ; в) 1,25; г) ∞; д) 0; е) 1; ж) -1/8;
з) 0,7; и) 27; к) 0,25; л) -6; м) 0,5. 24.2.
а) е8
; б) е; в) е-12
; г) 1; д) ∞; е) 1; ж) 0 ; з) 1/12; и) ∞ ; к)
-0,04; л) 0. 25.1.
а) 1; б)
![]() ; в) -2 ; г) 0 ; д) 42; е)
; в) -2 ; г) 0 ; д) 42; е)
![]() ;
ж) 12; з) 6; и) 0,25; к) 9 ; л) 1; м) е-2
. 26.1.
х=2 – точка устранимого разрыва. 26.2.
х=3 – точка разрыва II
рода
;
ж) 12; з) 6; и) 0,25; к) 9 ; л) 1; м) е-2
. 26.1.
х=2 – точка устранимого разрыва. 26.2.
х=3 – точка разрыва II
рода
26.3.
х=0 – точка неустранимого разрыва I
рода. 26.4.
х=0 – точка устранимого разрыва. 26.5.
функция непрерывна. 26.6.
х=-1 – точка устранимого разрыва, х=1 –
точка неустранимого разрыва I
рода. 26.7.
х=0 – точка разрыва II
рода. 27.1.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
27.2.
а)
.
27.2.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ; д)
; д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() ;
;
з)
![]() ; и)
; и)
![]() ; к)
; к)
![]() .
27.3.
а)
.
27.3.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
27.4. Касательная , нормаль . 27.5.
27.6.
![]() .
27.7.
.
27.7.
![]() .
27.8.
.
27.8.
![]() .
27.9.
.
27.9.
![]() .
27.10.
а)
.
27.10.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
27.11.
а) -1; б)
.
27.11.
а) -1; б)
![]() ;
в) -1; г)
;
в) -1; г)
![]() .
28.1.
а)
.
28.1.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
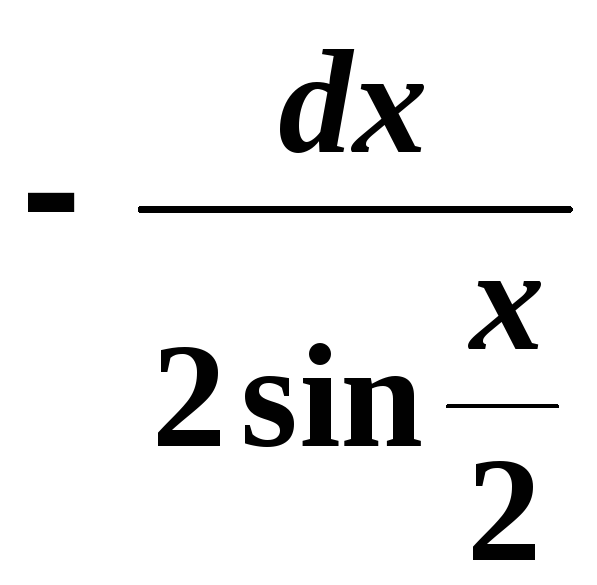 .
28.2.
а) 0,05; б) 0,00582 ; в) -0,24; г) -0,0693; д)
0,3466. 28.3.
а) 0,50025; б) 0,995; в)0,77; г) 0,355; д) 0,52164; е)
1,0025; ж) 1,15; з) 0,02. 28.4.
3% 29.1.
.
28.2.
а) 0,05; б) 0,00582 ; в) -0,24; г) -0,0693; д)
0,3466. 28.3.
а) 0,50025; б) 0,995; в)0,77; г) 0,355; д) 0,52164; е)
1,0025; ж) 1,15; з) 0,02. 28.4.
3% 29.1.
![]() .
29.2.
а)
.
29.2.
а)
![]() ; б)
; б)
![]() ;
в)
;
в)
![]() .
29.3.
а)
.
29.3.
а)
![]() ; б)
; б)
![]() .
29.4.
а)
.
29.4.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
29.5.
а)
.
29.5.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() .
29.6.
.
29.6.
![]() .
29.7.
а)
.
29.7.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)
![]() ;
г)
;
г)![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() ;
и)
;
и)
![]() ;
к)
;
к)
![]() .
.
29.8.
а) 0,4724; б) -0,5108; в) 2,0203; г) 0,309; д) 0,1974;
е) 0,9759. 30.1.
a)
0,5; б)
![]() ;
в) 0; г) 0; д) 1,6 ; е) 1; ж)
;
в) 0; г) 0; д) 1,6 ; е) 1; ж)
![]() ; з) 6 ; и) 1 ; к) -1. 30.2.
а) 0 ; б) 0; в) -1; г)
; з) 6 ; и) 1 ; к) -1. 30.2.
а) 0 ; б) 0; в) -1; г)
![]() ; д)
; д)
![]() .
.
30.3.
а) 0; б) 1 ; в) 1; г) 1. 31.1.
а)
![]() функция возрастает на
функция возрастает на
![]() и
и
![]() ,
убывает на
,
убывает на
![]() ;
б)
;
б)
![]() функция возрастает на
функция возрастает на
![]() и
и
![]() ,
убывает на
,
убывает на
![]() ;
в)
;
в)
![]() функция возрастает на
функция возрастает на
![]() ,
убывает на
,
убывает на
![]() ; г)
; г)
![]() функция возрастает на
функция возрастает на
![]() ,
убывает на
,
убывает на
![]() и
и
![]() ;
д)
;
д)
![]() функция возрастает на
функция возрастает на
![]() ,
убывает на
,
убывает на
![]() ;
е)
;
е)
![]() функция возрастает на
функция возрастает на
![]() и
и
![]() ,
убывает на
,
убывает на
![]() ; ж)
; ж)
![]() функция возрастает на
функция возрастает на
![]() ,
убывает на
,
убывает на
![]() и
и
![]() ;
з)
;
з)
![]() функция возрастает на
функция возрастает на
![]() ,
убывает на
,
убывает на
![]() ;
и)
;
и)
![]() функция
возрастает на
функция
возрастает на
![]() ,
убывает на
,
убывает на
![]() ;
к)
;
к)
![]() функция возрастает на
функция возрастает на
![]() ,
убывает на
,
убывает на
![]() .
31.2.
а)
.
31.2.
а)
![]() ; б)
; б)
![]() ;
;
в)
![]() ; г)
; г)
![]() ;
;
д)
![]()
31.3.
![]() ;
31.4.
;
31.4.
![]() .
.
31.5.
![]() .
31.6.
.
31.6.
![]() .
.
32.1.
a)
(0;0) и (1;2) – точки перегиба; функция
выпукла вверх на
![]() и
и
![]() ,
выпукла вниз на (0;1) ; б) (1;2) – точка
перегиба; функция выпукла вверх на
,
выпукла вниз на (0;1) ; б) (1;2) – точка
перегиба; функция выпукла вверх на
![]() ,
выпукла вниз на
,
выпукла вниз на
![]() ; в)
; в)
![]() - точки перегиба; функция выпукла вверх
на
- точки перегиба; функция выпукла вверх
на
![]() ,
выпукла вниз на
,
выпукла вниз на
![]() ;
г) (0;0) – точка перегиба; функция выпукла
вверх на
;
г) (0;0) – точка перегиба; функция выпукла
вверх на
![]() и
и
![]() ,
выпукла вниз на
,
выпукла вниз на
![]() и
и
![]() ; д) (0;0) и (2;0) – точки перегиба; функция
выпукла вверх на
; д) (0;0) и (2;0) – точки перегиба; функция
выпукла вверх на
![]() и
и
![]() ,
выпукла вниз на (0;2); е)
,
выпукла вниз на (0;2); е)
![]() - точка перегиба; функция выпукла вверх
на
- точка перегиба; функция выпукла вверх
на
![]() ,
выпукла вниз на
,
выпукла вниз на
![]() ;
ж) (0;0),
;
ж) (0;0),
![]() и
и
![]() - точки перегиба; функция выпукла вверх
на
- точки перегиба; функция выпукла вверх
на
![]() ,
(-1;0) и
,
(-1;0) и
![]() ,
выпукла вниз на
,
выпукла вниз на
![]() (0;1) и
(0;1) и
![]() ;
з)
;
з)
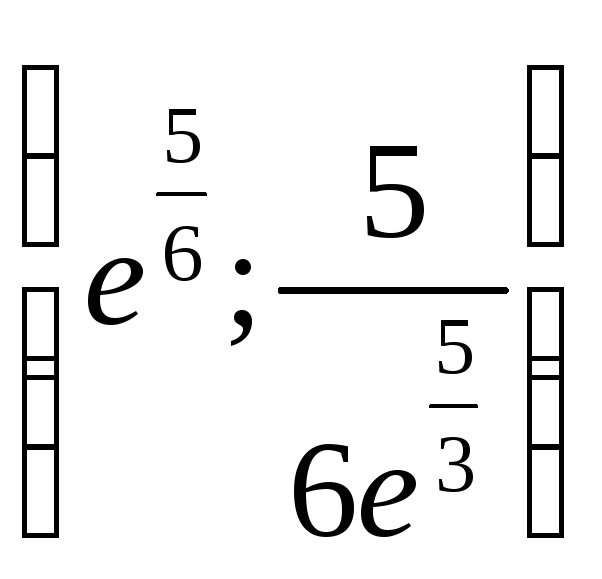 - точка перегиба; функция выпукла вверх
на
- точка перегиба; функция выпукла вверх
на
![]() ,
выпукла вниз на
,
выпукла вниз на
![]() ;
;
и)
![]() - точка перегиба; функция выпукла вверх
на
- точка перегиба; функция выпукла вверх
на
![]() ,
выпукла вниз на
,
выпукла вниз на
![]() ;
к) (-3;1) – точка перегиба; функция выпукла
вверх на
;
к) (-3;1) – точка перегиба; функция выпукла
вверх на
![]() ,
выпукла вниз на (-3;-2) и
,
выпукла вниз на (-3;-2) и
![]() .
33.1.
а)
.
33.1.
а)
![]() ; б)
; б)
![]() - правосторонняя;
- правосторонняя;
![]() - левосторонняя асимптоты ; в)
- левосторонняя асимптоты ; в)
![]() - правосторонняя асимптота ;
г)
- правосторонняя асимптота ;
г)
![]() - двусторонняя асимптота ; д)
- двусторонняя асимптота ; д)
![]() е) асимптоты отсутствуют
ж)
е) асимптоты отсутствуют
ж)
![]() - правосторонняя асимптота з)
- правосторонняя асимптота з)
![]() - двусторонняя асимптота.
- двусторонняя асимптота.
35.1.
а)
![]() ;
б)
;
б)
![]() ;
в)
35.2. а)
;
в)
35.2. а)
![]() ;
36.1. а)
;
36.1. а)
![]() ;
;
53.1.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
ж) 0. 53.2.
а) 0; б)
;
ж) 0. 53.2.
а) 0; б)
![]() ;
в) -8; г)
;
в) -8; г)
![]() ;
;
д) 28; е)
![]() ;
ж)
;
ж)
![]() .
54.2.
а)
.
54.2.
а)
![]() ;
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() .
55.1.
а)
.
55.1.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ;
ж)
;
ж)
![]() ;
з) 1)
;
з) 1)
![]() ;
2)
;
2)
![]() .
56.1.
а)
.
56.1.
а)
![]() ;
б)
;
б)
![]() ;
в) 8; г)
;
в) 8; г)
![]() ;
д) 4; е)
;
д) 4; е)
![]() ;
ж)
;
ж)
![]() ;
з)
;
з)
![]() ;
и)
;
и)
![]() .
.
60.3. а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
д)
;
д)
![]() ;
е)
;
е)
![]() ;
;
ж)
![]() ;
з)
;
з)
![]() ;
;
и)
![]() ;
к)
;
к)
![]() .
.
61.1.
а)![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
е)
;
е)
![]() ж)
ж)![]() ;
;
з)
![]() .
.
61.2.
а)![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
62.1.
а)![]() ;
б)
;
б)
![]() ;в)
;в)
![]() ;
г)
;
г)
![]() ;
д)
;
д)
![]() .
62.2.
.
62.2.
![]() ;
б)
;
б)
![]() .
.
63.1.
а)![]() ;б)
;б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() ;
;
д)
![]() .
63.2. а)
.
63.2. а)![]() ;
б)
;
б)
![]() ;в)
;в)![]() .
63.3.
.
63.3.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]()
64.1.
а)
![]() ;
б)
;
б)![]() ;
в)
;
в)![]() ;
;
г)
![]() .
64.2. а)
.
64.2. а)
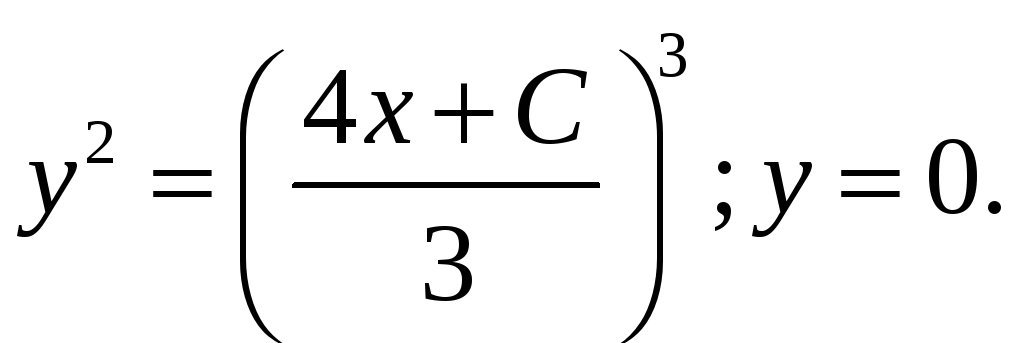 ;
б)
;
б)
![]()
![]() ;
в)
;
в)
![]()
![]() ;г)
;г)
![]()
![]() ;
;
д)
![]() ;
е)
;
е)
![]()
![]() ;
ж)
;
ж)
![]()
![]() ;
з)
;
з)
![]()
![]()
65.1.
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() .
65.2. а)
.
65.2. а)![]() ;
;
б)
![]() ;
в)
;
в)
![]() ;
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
ж)
;
ж)
![]() ;
;
з)
![]() .
65.3. а)
.
65.3. а)
![]() ;
;
б)
![]() ;
в)
;
в)
![]() .
.
66.1.
а)![]() ;
б)
;
б)
![]() ;
в)
;
в)![]() ;
г)
;
г)
![]() ;
;
д)
![]() ;
;
е)
![]() ;
;
ж)
![]() ;
;
з)
![]() ;
;
и)
![]() ;
;
к)
![]()
