Силы трения.

Силы трения возникают при относительном перемещении соприкасающихся тел или при движении тел в непрерывных средах (газа или жидкости). Различают силы сухого и вязкого трения. Сухое трение возникает между твёрдыми телами, вязкое – между телом и жидкостью или газом, а также между слоями жидкости или газа. Силы трения направлены вдоль поверхности соприкасающихся тел и противоположны скорости их относительного движения.

Сухое трение.

Сухое трение подразделяется на трение покоя, скольжения и качения.

Трение покоя.

Величина и направление силы трения покоя определяется направлением и величиной внешней силы. Сила трения покоя направлена против внешней силы и равна ей по величине. Предельная сила трения покоя пропорциональна силе нормального давления:

,

направлена против внешней силы. Здесь - коэффициент трения покоя, величина безразмерная, зависит от природы соприкасающихся тел, механического состояния поверхностей,…

Трение скольжения.

Сила трения скольжения направлена против скорости относительного движения трущихся тел, пропорциональна силе нормального давления

,

где - коэффициент трения скольжения, величина безразмерная, зависит от механического состояния трущихся поверхностей, их природы и примесей.

скольжения немного меньше .

При решении конкретных задач обычно не делают различия между и, считая их одинаковыми.

Сила трения скольжения слабо зависит от скорости относительного движения, поэтому этой зависимостью обычно пренебрегают. Силу трения скольжения можно представить в виде:

.

Трение качения.

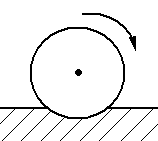Трение качения возникает при качении круглых тел по поверхности. Эксперименты показывают, что величина силы трения качения пропорциональна силе нормального давления, обратно пропорциональна радиусу круглого тела и направлена против качения:

,

здесь - коэффициент трения качения, , зависит от природы поверхности и катящегося тела.

Механизм трения качения связан с деформацией поверхности и катящегося тела и преодолением возникающих при этом барьеров. Для твёрдых тел трение качения, очевидно, равно нулю. Для реальных тел и поверхностей трение при качении всегда присутствует, но оно существенно меньше трения скольжения. Поэтому, где это возможно, скольжение пытаются заменить качением. Несмотря на такую выгоду природа не «додумалась» до этого. Изобретение колеса человеком – это величайшее открытие. В практических задачах трением качения обычно пренебрегают по сравнению с трением скольжения. Но есть задачи, в которых трением качения принципиально пренебречь нельзя (Какие это задачи? Подумайте).

Вязкое трение.

В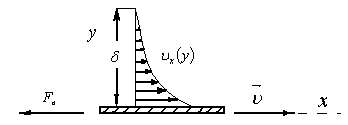язкое трение возникает при движении тел в жидкостях и газах. Механизм вязкого трения связан с прилипанием жидкости к телу. Жидкость при этом увлекается телом, а тело теряет свой импульс. В неподвижной жидкости при этом поперёк движения тела возникает перепад скорости. Скорость жидкости у поверхности тела равна скорости тела и чем дальше от тела поперёк его движения, тем меньше скорость жидкости (см.рисунок).

Слой жидкости в пределах которого наблюдается перепад скорости обычно невелик и называется пограничным слоем (- толщина пограничного слоя).

Толщина пограничного слоя у поверхности тела будет определяться скоростью движения тела , вязкостью жидкости и её плотностью . Из соображений размерности:

~.

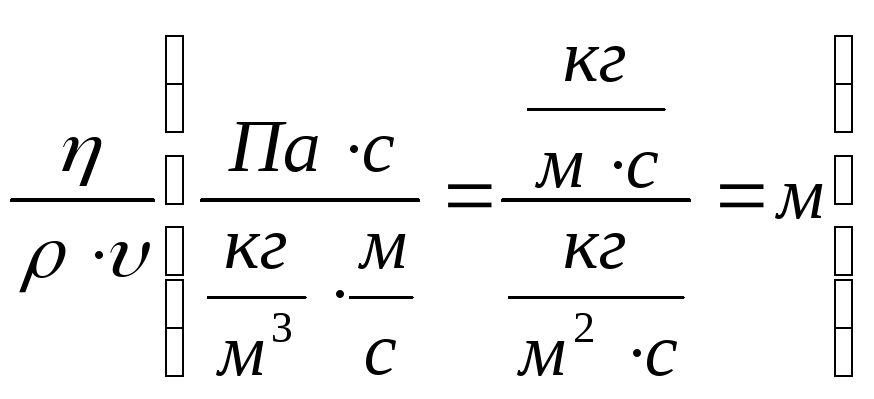Пространственное изменение скорости характеризуется изменением величины скорости в направлении , приходившееся на единицу длины , который называется градиентом скорости. Между слоями жидкости возникает вязкое трение (слоистое течение жидкости называется ламинарным), которое пропорционально градиенту скорости:

(закон Ньютона для вязкого трения в случае ламинарного течения); - сила вязкого трения, приходящаяся на единицу поверхности между слоями жидкости; - коэффициент пропорциональности, отражающий свойство жидкости, называется вязкостью жидкости; численно равен при . Вязкость измеряется в : .

На тело при движении в жидкости будет действовать сила вязкого трения, которая, очевидно, будет зависеть от скорости его движения , его формы и размеров и вязкости жидкости :

,

где - зависит от геометрических размеров тела и вязкости жидкости.

В случае шара, геометрия которого однозначно определяется его радиусом , коэффициент . Из анализа размерности сила вязкого трения, действующая на движущийся шар в жидкости, пропорциональна следующему выражению, составленному из :

~.

Проверьте размерность правой части соотношения. Точный гидродинамический расчёт даёт для величины силы вязкого трения:

.

Это соотношение называется формулой Стокса. *Стокс Джордж Габриель(13.08 1819-1.021903) – английский физик и математик. Разработал в 1845 году теорию вязкости жидкости, теорию движения вязкой жидкости, вывел формулу силы вязкого трения, действующую на шар, движущийся поступательно в жидкости с небольшой скоростью (формула Стокса).*

Эту формулу в лабораторном практикуме мы будем использовать для экспериментального определения вязкости глицерина.