Однородное поле тяжести Земли.
При движении тел вблизи поверхности
Земли изменением ускорения свободного
падения можно пренебречь и считать
.
Такое поле тяжести называется однородным.
Оценим высоту h, до которой
с точностью до 1% можно принимать
.
Рассмотрим зависимость
:
,
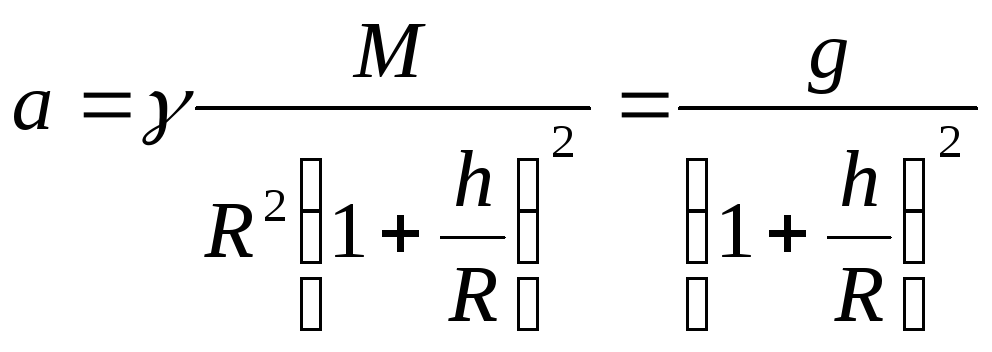при
.
при
.
Для всех высот h<=32км
поле тяжести Земли с погрешностью до
1% можно считать однородным и принимать
.
Для высот сравнимых с радиусом Земли
уменьшением ускорения свободного
падения пренебречь нельзя. Например,
при h=R
.
Отмети, что ускорение свободного у
поверхности Земли изменяется с широтой,
что связано с вращением Земли и её
приплюснутостью у полюсов. Аномальное
значение g наблюдается в
местах пустот и массивных залежей в
недрах Земли. Измерение отклонения g
от стандартного значения позволяет
обнаружить эти аномалии в распределении
массы. Измерение g
эквивалентно «взвешиванию» Земли
.
Понятие веса тела.
Если тело связано нитью или находится на подставке, то под действием силы тяжести тело действует с некоторой силой на связи (растягивает нить, деформирует подставку). Сила, с которой тело действует на связи в результате притяжения к Земле, называется весом тела.
Вес – это статическое проявление силы тяжести, связанное с деформацией связей. Сила тяжести может полностью расходоваться на сообщение ускорения (динамическое проявление силы). В этом случае вес тела равен нулю. Это состояние называется невесомостью. Свободно падающее тело находится в состоянии невесомости. На ИСЗ и космических станциях наблюдается невесомость. Вес тела может многократно превышать силу тяжести. Такое состояние называется перегрузкой. Например, в лифте падающем с ускорением a<g, вес тел меньше силы тяжести, при a=g вес равен нулю; если лифт поднимается вверх с ускорением, то вес тела больше силы тяжести. (обоснуйте самостоятельно эти утверждения).
Упругие деформации. Закон Гука.
В результате контактного взаимодействия тела деформируются. Деформации условно подразделяются на упругие и неупругие. При упругих деформациях тела после взаимодействия восстанавливают прежние размеры и форму. При неупругих деформациях имеет место остаточные деформации. Различают следующие виды деформации:
-
растяжения-сжатия,
-
изгиба,
-
кручения,
-
сдвига.
Все виды деформаций, в конечном счёте сводятся к деформациям растяжения-сжатия и сдвига.
На практике наиболее часто встречаются деформации растяжения-сжатия, которые связаны с изменением объёма (длины) тела под действием силы.
При упругой деформации изменение длины тела пропорционально приложенной к нему силе:
~
.
При деформации возникает сила противодействия (упругая сила), направленная в обратную сторону деформации и пропорциональная величине деформации (закон Гука):
,
где коэффициент пропорциональности k зависит от природы тела, его геометрических размеров, термического состояния, называется коэффициентом упругости.
Коэффициент k численно
равен F, при
,
измеряется в
.
Коэффициент упругости зависит от природы тела и его геометрических размеров. Найдём эту зависимость. Упругие напряжения в теле
пропорциональны относительному
удлинению
:
,
где E – модуль Юнга,
определяется природой тела и равно
напряжению P при
,
.
Подставим в выражение для упругих
напряжений значения P и
:
,
откуда получаем
.
Следовательно,
,
где k~S –
площадь поперечного сечения тела,
-
длина недеформированного тела.
Упругие силы – результат статического действия внешних сил, приложенных к телу. В случае одномерной деформации, например пружины:
или
,
где x – изменение длины пружины от недеформированного состояния.
Упругие силы по своей природе являются электрическими, т.е. в основе упругих сил лежат электрические взаимодействия между атомами и молекулами вещества.