Интегральное выражение основного закона динамики. Понятие импульса силы.

Действие силы во времени характеризуется произведением силы на время её действия. Элементарный импульс силы равен .

Из основного закона динамики точки следует

- импульс силы равен изменению импульса частицы.

Для конечного промежутка времени:

,

.

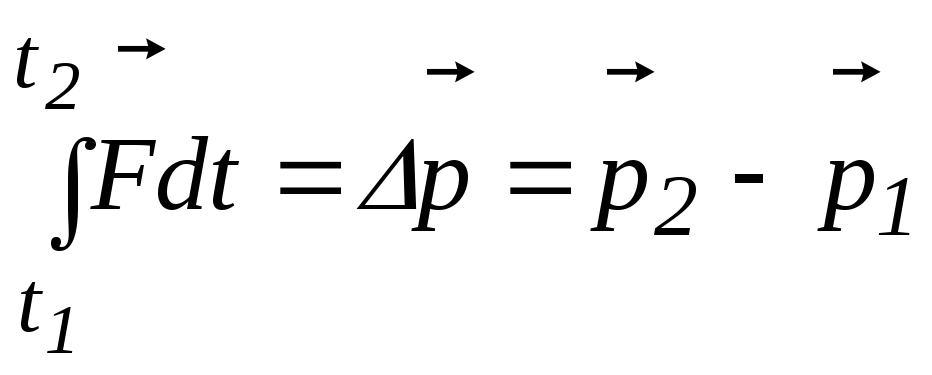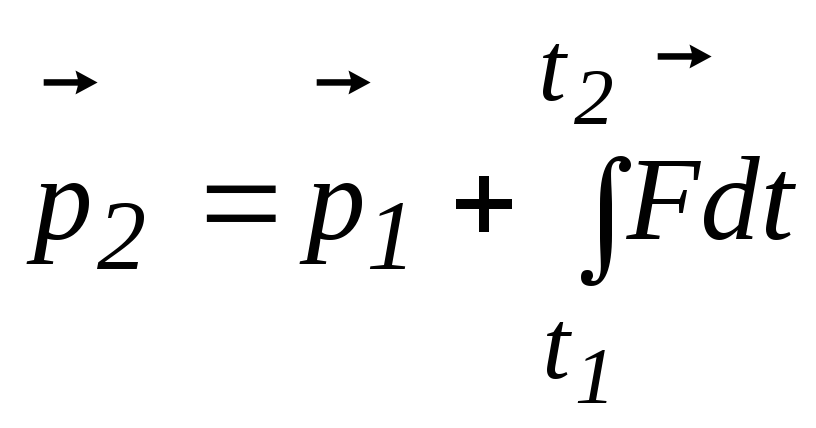Последнее соотношение является интегральным выражением основного закона динамики точки и может быть представлено как:

,

где 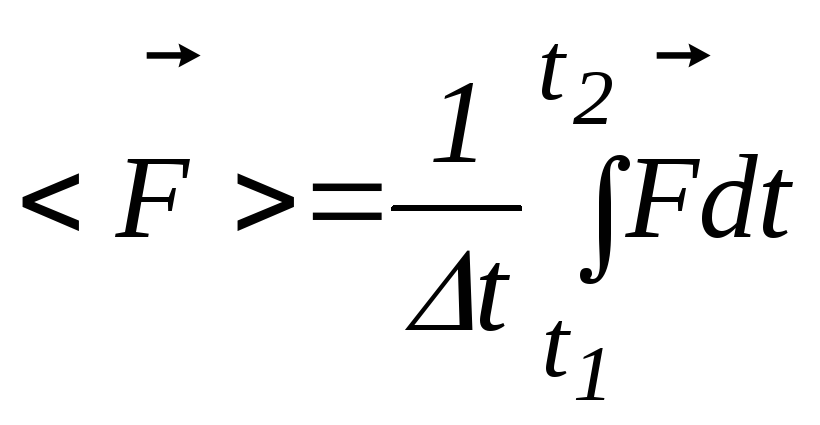- средняя сила для промежутка времени .

Графическая иллюстрация:

1) ,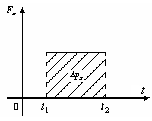

,

.

2)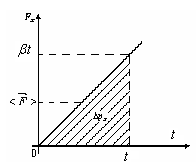

,

,

,

.

3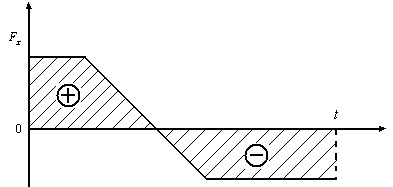) алгебраическая сумма площадей «+» и «-».

Третий закон Ньютона.

Взаимодействующие частицы выступают как равные партнёры; действие одной из них на другую равно действию второй на первую: сила действия равна силе противодействия

или .

Эти силы приложены к разным частицам.

Третий закон Ньютона справедлив не всегда. Он верен только для тел (частиц), взаимодействующих непосредственным соприкосновением. Он также верен для взаимодействий на расстоянии (за счёт центральных сил), если частицы (тела) взаимно покоятся.

Для движущихся тел III закон Ньютона тем точнее, чем меньше отношение

. Для нецентральных сил (магнитная сила) III закон Ньютона не выполняется. III закон Ньютона не выполняется в области микромира (понятие силы теряет смысл).

Динамика систем материальных точек. Обобщение II закона Ньютона для системы материальных точек. Импульс системы. Закон сохранения импульса системы.

Рассмотрим систему N взаимодействующих частиц.

Силы взаимодействия меду частицами системы будем называть внутренними. Силы взаимодействия частиц системы с частицами, не входящими в систему – внешними.

Система частиц, не испытывающая внешних взаимодействий, называется замкнутой или изолированной. Замкнутые системы – это физическая абстракция. В конкретной ситуации понятие замкнутости применяется возможностью пренебречь внешними воздействиями на систему.

Запишем II закон Ньютона для каждой частицы системы с учётом парных взаимодействий между частицами системы и внешней силы:

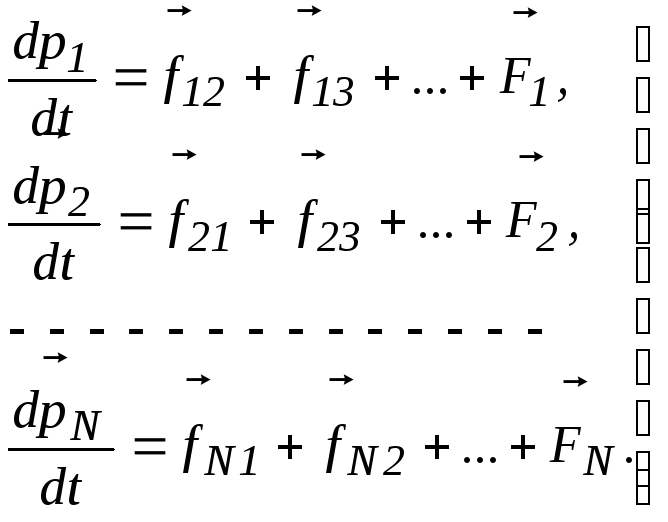
Согласно III закона Ньютона

Сложим левые и правые части записанных выражений с учётом III закона Ньютона:

или

- суммарный импульс частиц системы.

- сумма внешних сил.

Тогда для системы частиц можно записать:

.

Полученное выражение формально совпадает с выражением II закона Ньютона для частицы, поэтому его можно интерпретировать как обобщение II закона Ньютона для системы частиц.

Импульс системы является векторной мерой движения системы в целом и является величиной аддитивной.

Изменение импульса системы определяется внешними силами, т.е. внутренние силы не изменят полного импульса системы.

В случае замкнутой системы имеем , то есть

,

импульс замкнутой системы сохраняется. Импульс явно не зависит от времени.

Но это не означает, что импульс каждой частицы остаётся неизменным. Под действием внутренних сил импульс частиц изменяется, наблюдается перераспределение импульса между частицами, они непрерывно обмениваются импульсами, но при этом их сумма не изменяется.

Это фундаментальный закон природы, связанный с однородностью пространства, не имеет исключений, даже, если не выполняется III закон Ньютона.