Энтропия.

Рассмотрим равновесный круговой процесс (см. рисунок) 1а2в1. запишем теорему Клаузиуса для этого процесса:

.

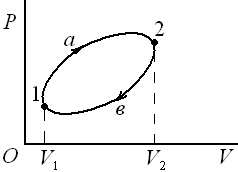Перенесём одно из слагаемых в правую часть равенства и изменим у него направление интегрирования на противоположное, что изменит знак у интеграла. Тогда получим равенство следующего вида:

.

Это равенство показывает, что приведённое тепло, взятое по обратимому процессу, не зависит от промежуточных состояний процесса, а зависит только от его начального и конечного состояний. Это свойство приведённого тепла означает, что его в обратимом процессе можно рассматривать как изменение некоторой функции состояния. Эта функция состояния называется энтропией и обозначается буквой . Итак, по определению:

, .

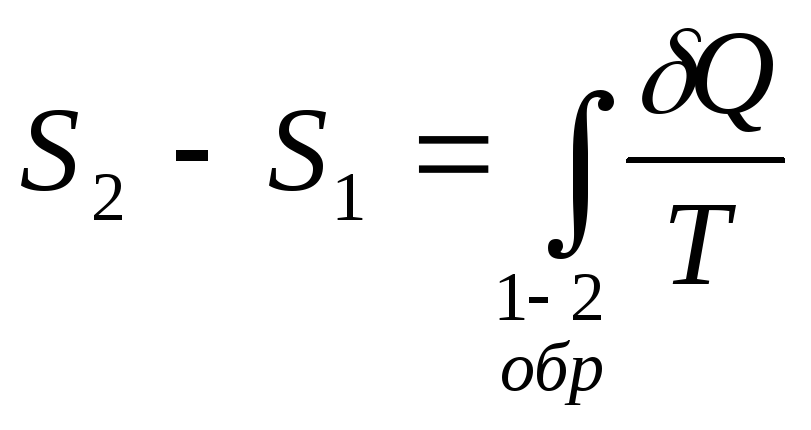Энтропией называется функция состояния термодинамической системы, изменение которой равно приведённому теплу, взятому по обратимому процессу, соединяющему рассматриваемые состояния. В этом определении говорится лишь об изменении энтропии. Чтобы определить абсолютное значение энтропии нужен дополнительный постулат. Это теорема Нернста: при приближении к нулю абсолютной температуры энтропия любого тела стремится к нулю.

Отметим, что данное определение энтропии является сугубо формальным. Энтропию нельзя измерить. Изменение энтропии можно вычислить. Для этого два состояния соединяют подходящим равновесным процессом и производят вычисления.

Некоторую наглядность и физический смысл энтропия получает в рамках статистической физики.

Теперь обратимся к следствию из теоремы Клаудиуса для необратимого кругового процесса:

.

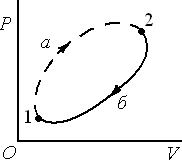Рассмотрим круговой процесс, состоящий из необратимого участка 1а2 и обратимого участка 2б1 (см. диаграмму).

Представим приведённую теплоту кругового процесса как сумму:

.

Перенесём второе слагаемое в правую часть и изменим направление интегрирования, так процесс 2б1 является обратимым:

.

Следовательно,

.

Изменение энтропии равно приведённому теплу при обратимом процессе, но больше приведённого тепла при необратимом процессе. В общем случае можно записать:

, ,

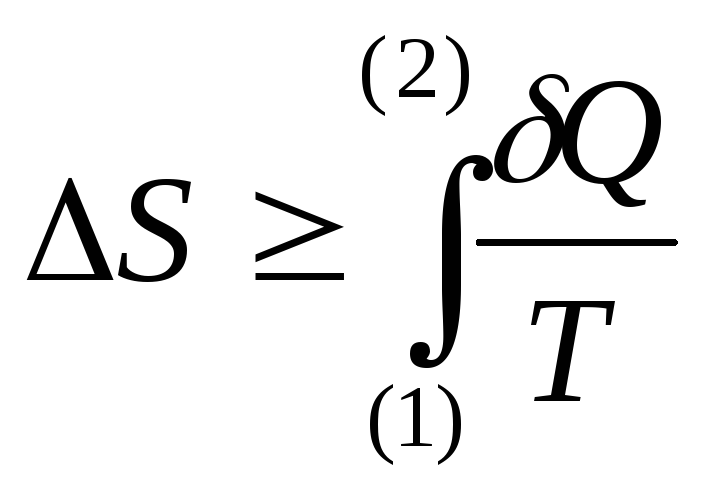где знак «=» относится к обратимому процессу, а знак «>» - к необратимому.

Для адиабатической системы и, следовательно, или .

Мы получили важное следствие: в адиабатических системах энтропия в обратимых процессах остаётся постоянной, а в необратимых возрастает. Но, поскольку обратимых процессов в природе не существует, то можно сделать заключение, что во всех реальных адиабатных процессах энтропия обязательно возрастает. Это утверждение называется законом роста энтропии и является наиболее общей формулировкой II н.т.д. для изолированных т.д.с.

Этот закон до некоторой степени приоткрывает физический смысл понятия энтропии. Одностороннее изменение энтропии связано с необратимостью процессов в адиабатических системах. Энтропия есть величина, обусловленная необратимостью термодинамических процессов: то, что вызывает необратимость, ведёт к существованию энтропии и её росту. Это процессы релаксации. В процессе релаксации макросистема переходит от менее вероятных состояний к более вероятным. Отметим, что энтропия является величиной аддитивной: энтропия тела равна сумме энтропий его частей: . Это связано с аддитивностью количества тепла, а температура в равновесии для всех частей тела одинакова.

Кроме того, энтропия является однозначной и монотонной функцией внутренней энергии. Выразим:

.

При :

.

Так как и положительная величина , то, следовательно, , т.е. .