Динамика.

Динамика материальной точки.

В основе динамики в классической механике лежат три закона Ньютона, известные вам из школьного курса физики. Вспомним эти законы и динамические понятия, а также проследим за логикой построения классической механики, обозначим пределы её применяемости, расширим и уточним некоторые понятия…

Первый закон Ньютона. Инерциальные системы отсчёта (исо). Принцип относительности. Преобразования Галилея.

Первый закон Ньютона (его также называют законом инерции) утверждает, что свободная частица движется равномерно и прямолинейно или покоится.

Свободная частица – это частица, не взаимодействующая с другими частицами и полями. Понятие «свободная частица» - это физическая абстракция, которая применяется, когда взаимодействиями с другими частицами и полями можно пренебречь.

С другой стороны закон инерции является определением инерциальных систем отсчёта (ИСО): системы отсчёта, в которых свободная частица покоится или движется равномерно прямолинейно, называются инерциальными системами отсчёта.

ИСО множество и все они эквивалентны.

В этом и заключается существо механического принципа относительности: любое механическое движение протекает тождественно во всех ИСО, т.е., находясь в ИСО, невозможно обнаружить, движется она или покоится.

Законы механики во всех ИСО имеют один и тот же вид, т.е. не меняются при переходе от одной ИСО к другой. Такие физические величины и соотношения, которые не меняются при переходе из одной ИСО в другую, называются инвариантами (invar).

Координаты и время при переходе от одной ИСО (S) к другой (), которая движется относительно первой со скоростью , преобразуются следующим образом:

,

,

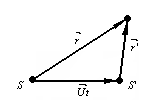которые называются преобразованиями Галилея.

Время во всех ИСО течёт одинаково (время абсолютно), однородно, что позволяет начало отсчёта времени выбирать произвольно, т.к. все моменты времени эквивалентны, т.е. ни один момент времени физически не выделен. Время всегда течёт в одну сторону (t>0), измеряется с помощью часов, в основе которых лежит какой-либо периодический процесс: колебание, вращение.

Такое представление о времени является приближённым и годится только для описания механического движения со скоростями (скорость света в вакууме – предельная скорость в природе).

В S и S’ интервалы времени являются инвариантами , также инвариантами являются расстояния (длины):

для одного и того же момента времени :

.

Скорость является относительной величиной и преобразуется согласно закону сложения скоростей:

, , =,

.

В СТО интервалы времени и расстояния оказываются относительными величинами, а скорость частиц преобразуется по более сложным соотношениям, которые при переходят в классическое приближения Ньютона согласно принципу соответствия.

В динамике вводятся динамические физические величины. Вспомним их и уточним их физический смысл.

Импульс частицы (количество движения)

Это векторная мера механического движения, равная

,

где - скорость частицы, - коэффициент пропорциональности, отражающий свойства частицы.

- масса частицы, величина скалярная, неотрицательная, является инвариантом. Импульс измеряется в .

Импульс – величина относительная. Если в S системе , то в системе S’

.

В соответствии с законом инерции импульс свободной частицы в ИСО в процессе движения не изменяется:

, т.к. .

В законе инерции и сохранения импульса свободной частицы проявляется свойство однородности пространства (все точки пространства равноценны).