Политропный процесс.
Этот процесс объединяет всевозможные равновесные процессы с идеальным газом и описывается уравнением вида:
,
где
- действительное число называемое
степенью политропы.
Политропный процесс содержит, как
частные случаи, известные изопроцессы.
Например, значению
соответствует изотермический процесс,
- изобарный,
- изохорный,
- адиабатный.
Работа политропного процесса.
,
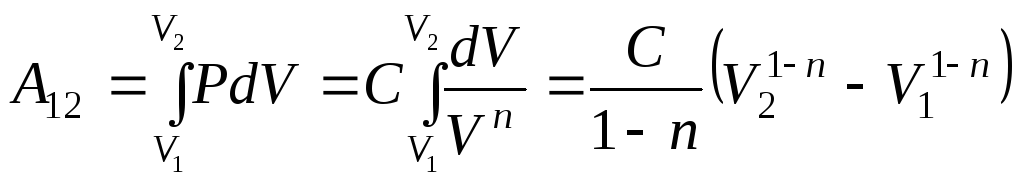кроме
.
Заменяя
,
получаем:
.
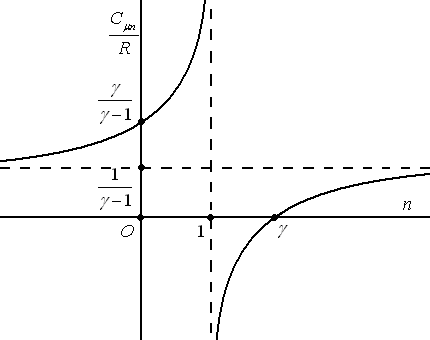Другие
альтернативные выражения для работы
политропного процесса можно получить,
комбинируя уравнение политропы и
уравнение состояния идеального газа.
Например:
.
Теплота политропного процесса может быть найдена, согласно соотношению:
,
где
- молярная теплоёмкость политропного
процесса.
Найдём зависимость
от степени политропного процесса
.
Воспользуемся первым началом термодинамики:
,
.
Следовательно,
.
Зависимость
от
представлена на рисунке.
Отметим, что теплоёмкость может принимать
отрицательные значения для значений
,
т.е. для всех политроп между изотермическим
и адиабатным процессами. Это означает,
что идеальный газ может нагреваться
при отборе у него тепла. Такой нагрев
может происходить за счёт внешней
работы.
Нетрудно получить выражение для степени политропы через теплоёмкости:
.
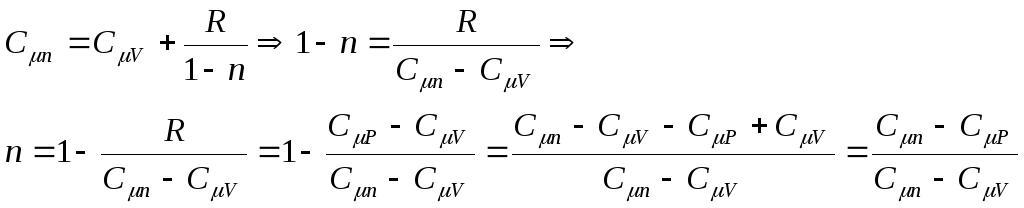
Круговые процессы. Цикл Карно. Кпд тепловых машин.
В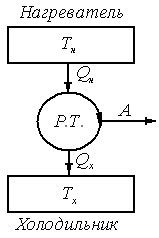
технической термодинамике и теплотехнике
большую роль играют циклические процессы,
после завершения которых система
возвращается в исходное положение. Это
обусловлено тем, что машинами непрерывного
действия могут быть только циклично
работающие машины.
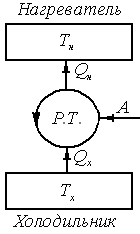
Тепловые машины подразделяются на
тепловые двигатели и холодильные
установки или тепловые насосы. В принципе
работа тепловой машины может быть
сведена к взаимодействию трёх элементов:
нагревателя, холодильника и рабочего
тела. Тепловой двигатель (см. рисунок)
предназначен для преобразования тепла
в работу:
,
если
.
Так как
,
а
,
то
или
.
Работа теплового двигателя равна
разности тепла, взятого от нагревателя
и тепла, переданного холодильнику:
.
Эффективность теплового двигателя определяется его коэффициентом полезного действия:
.
Если
тепловую машину запустить в обратном
направлении, то она будет работать как
холодильная установка или тепловой
насос (см. рисунок).
Холодильные установки предназначены
для производства «холода» или тепла за
счёт внешней работы
.
При этом происходит отбор тепла от
холодильника и передача его нагревателю:
.
Эффективность холодильной установки определяется соотношением:
,
а теплового насоса:
.
Отметим, что в реальных условиях, роль холодильника для тепловых двигателей и роль нагревателя для холодильных установок играет окружающая среда.
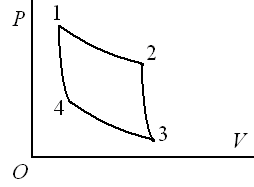При
наличии одного нагревателя и одного
холодильника может быть выполнено
множество различных циклов. Но в этом
множестве можно выделить один цикл,
называемый циклом Карно, состоящий из
двух изотерм и двух адиабат (см. диаграмму),
где 1-2 изотерма при
,
3-4 изотерма при
,
2-3 и 4-1 адиабаты между температурами
и
.
Роль цикла Карно заключается в том, что
это единственный цикл между нагревателем
и холодильником, который может быть
выполнен обратимым образом.
Обратимым называется процесс, который может быть проведён в прямом и обратном направлении через одну и ту же совокупность промежуточных состояний без остаточных изменений в окружающей среде. Все равновесные процессы являются обратимыми. Обратимые процессы – физическая абстракция. Реальные процессы являются необратимыми.
Вернёмся к циклу Карно. Обратимый теплообмен между телами возможен только при изотермическом процессе. Наличие конечной разности температур между телами делает передачу тепла необратимой, так как невозможен самопроизвольный переток тепла от холодного тела к нагретому. В цикле Карно представлены два изотермических процесса, являющиеся обратимыми, и два адиабатных процесса, протекающих без теплообмена. Таким образом, действительно цикл Карно является единственным обратимым циклом, который можно провести между одним нагревателем и одним холодильником.
Определим КПД цикла Карно. В качестве рабочего тела выберем идеальный газ. Работа за цикл равна:
,
где
,
,
,
.
Так как в адиабатическом процессе
,
то
Следовательно
.
Так как
,
то работа за цикл равна:
.
Теплота, взятая от нагревателя, равна:
.
Таким образом, КПД теплового двигателя Карно равен:
.
Отметим, что реальные тепловые машины не работают по циклу Карно, а используют другие (технические) циклы. Это связано с тем, что машина Карно маломощна. Но в теплотехнике она играет важную роль, так как устанавливает теоретический предел для КПД реальных машин.
Лекция 15.