Температура

Понятие «температура» занимает центральное место в учении о тепловых процессах. Оно является довольно сложным, и длительное время уточнялось по мере развития термодинамики и статистической физики. Например, понятие температуры как «степени нагретости» тела имеет явно выраженный субъективный аспект. Объективная возможность введения понятия температуры связана со свойствами теплового равновесия. Состояния теплового равновесия отличаются друг от друга. Мерой теплового равновесия является температура.

Температура как мера теплового равновесия обладает следующими свойствами:

1. если ТДС (тела) А и В не находятся в состоянии теплового равновесия и при тепловом контакте наблюдается переход энергии от А к В, то .

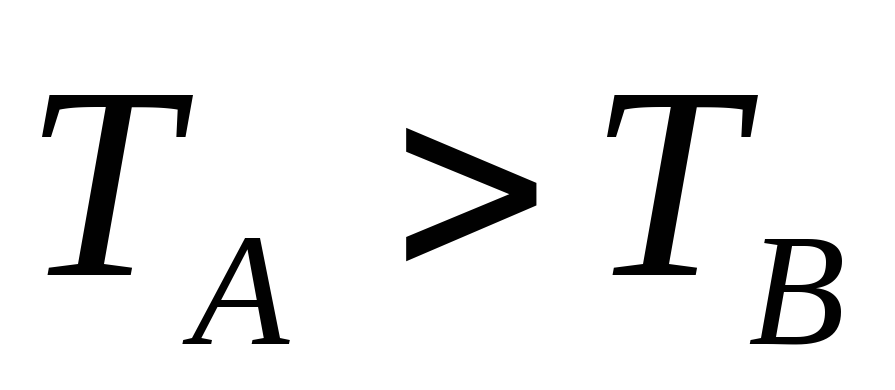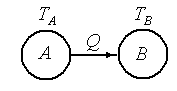
2. если совместная система (А+В) является изолированной, то с течением времени наступит новое состояние равновесия с температурой .

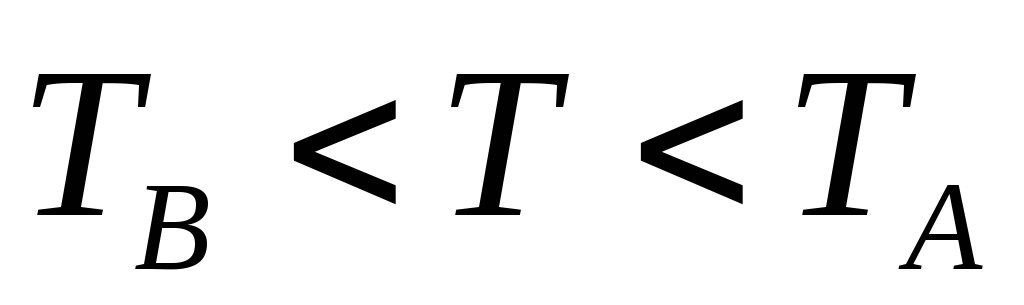3. если при тепловом контакте тел А и В не наблюдается перехода энергии (Q=0), то А и В находятся в одинаковом состоянии теплового равновесия (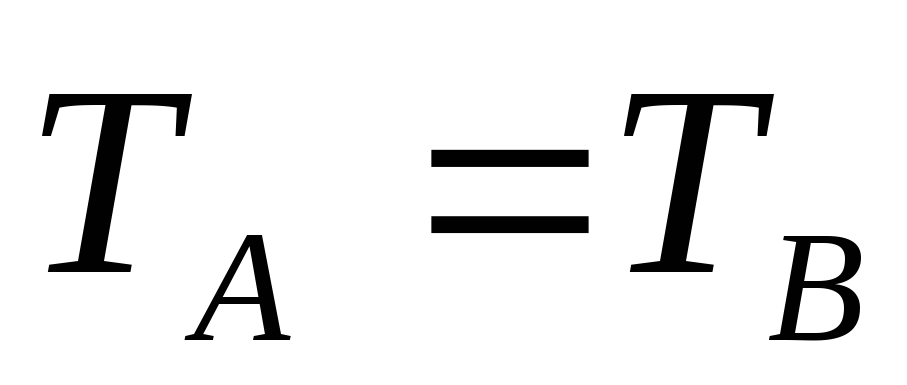). Если при тепловом контакте В и С Q=0, то 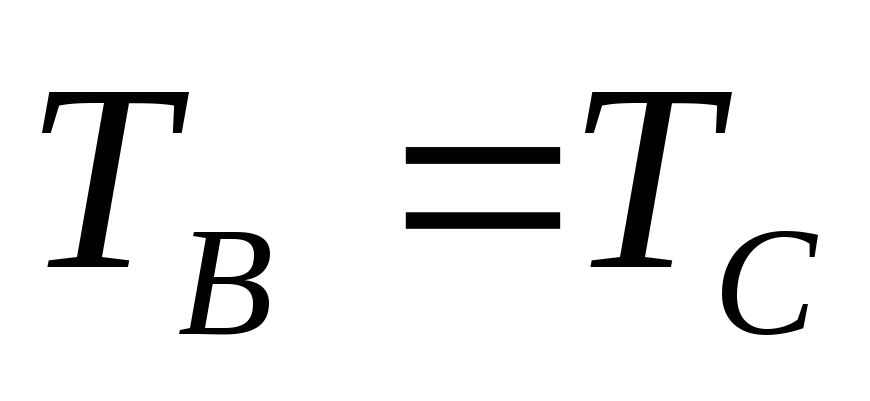, т.е. 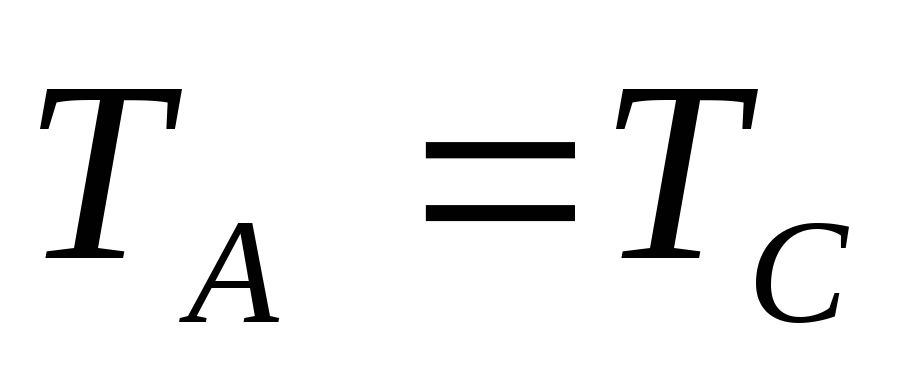.Тепловое равновесие обладает свойством транзитивности.

Тепловое равновесие не зависит от объёма, давления, плотности и других величин, определяющих состояние системы. Оно однозначно определяется температурой, которая относится к числу внутренних параметров системы, является макроскопической характеристикой системы в целом и для отдельной молекулы смысла не имеет.

В отличие от многих других физических величин температура не может быть измерена непосредственно. Измерение температуры производится косвенными методами, основанными на физических свойствах тел, которые могут быть измерены непосредственно. Тело, выбираемое для измерения температуры, называется термометрическим, а физическая величина, используемая для измерения температуры – термометрическоё величиной. Например, в медицинском термометре термометрическим телом является ртуть, а термометрической величиной – объём столба ртути. Увеличение объёма термометрического тела при нагревании даёт косвенную информацию об изменении температуры.

Если зависимость объёма тела (газа) от температуры линейная, то достаточно выбрать две реперные точки, приписать этим точкам определённые значения температуры, а полученный интервал разделить на некоторое число промежутков. По такому принципу строится любая эмпирическая шкала температуры (Цельсия, Реомюра, Фаренгейта).

Очевидно, подобные температурные шкалы являются условными. Например, современный вариант шкалы Цельсия строится на двух реперных точках: температура таяния льда и кипения воды при нормальном давлении. При использовании различных термометрических тел точные значения температура имеет только для реперных точек, для промежуточных точек наблюдается расхождение. Наиболее точными являются газовые термометры, использующие достаточно разрежённый (идеальной) газ.

Средняя кинетическая энергия поступательного движения молекул газа обладает всеми свойствами температуры. Поэтому в качестве температуры можно использовать величину пропорциональную средней энергии 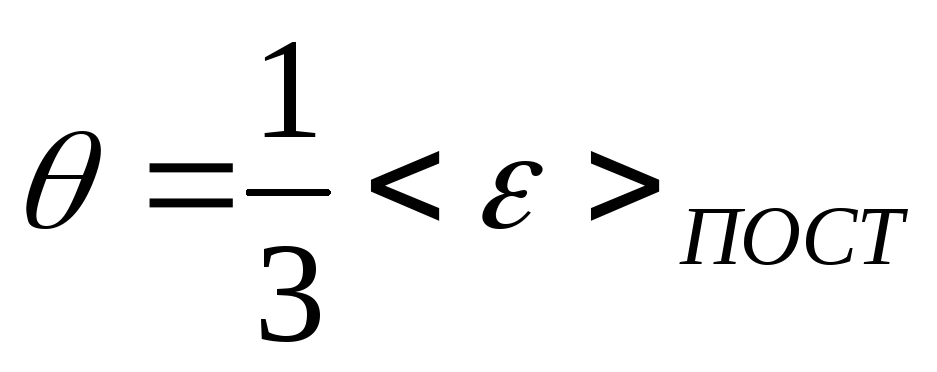, выраженную непосредственно в . При таком определении многие формулы теоретической физики и термодинамики упрощаются и в теоретических исследованиях часто так и поступают. Однако, для практических целей измерение температуры в энергетических единицах неудобно. Например, нормальная температура человеческого тела в энергетических единицах равна . Поэтому сохранена привычная система измерения температуры в градусах.

С точки зрения МКТ абсолютная температура есть мера средней кинетической энергии поступательного движения молекул тела. В случае идеального газа абсолютная температура в К (Кельвин) равна:

,

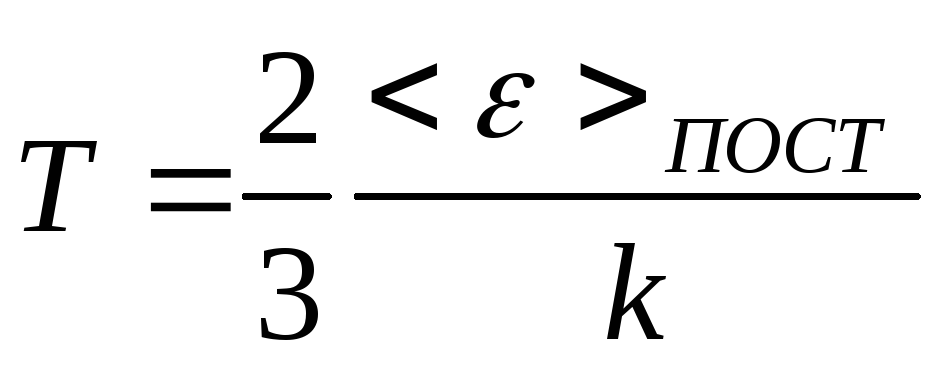где - постоянная Больцмана, является переводным коэффициентом между и .

При таком определении температуры нулю абсолютной температуры соответствует , таким образом, средняя кинетическая энергия поступательного движения молекул пропорциональна абсолютной температуре:

.

Используя последнее соотношение, выразим основное уравнение МКТ идеального газа через абсолютную температуру:

.

Давление газа пропорционально концентрации молекул ~ и абсолютной температуре ~. При температура является однозначной функцией давления. Измерив давление газа, можно вычислить температуру. На этом принципе основано измерение абсолютной температуры с помощью газового термометра, который использует газ, близкий по свойствам к идеальному (достаточно разрежённый газообразный водород).

При построении абсолютной шкалы используется единственная реперная точка – тройная точка воды, которая соответствует равновесию системы, состоящей из льда, воды и водяного пара. Единица измерения температуры (1 Кельвин) выбирается так, чтобы температура тройной точки воды оказалась точно на 273,16 К выше абсолютного нуля температуры.

Температура замерзания воды при нормальном давлении по абсолютной шкале равна . Поэтому переход к температурам Цельсия даётся формулой . При этом .