Модель идеального газа. Уравнение состояния идеального газа.

Газ как макроскопический объект не имеет собственного объёма, представляет собой совокупность молекул, движение которых подчиняется законам классической механики.

Если некоторая масса газа m занимает объём V, при заданной температуре T, в этом объёме устанавливается давление P. Величины m, P, V, T и являются макроскопическими параметрами газа. Эти параметры связаны уравнением состояния газа. В случае однородного и достаточно разреженного газа из частных эмпирических газовых законов было получено уравнение состояния газа:

,

где M – молярная масса газа, - универсальная газовая постоянная.

Это уравнение, известное школьникам как уравнение Клапейрона-Менделеева, является уравнением состояния идеального газа.

Основное уравнение молекулярно-кинетической теории идеального газа.

Молекулярно-кинетическая теория позволяет описать свойства идеального газа и вывести его уравнение состояния. При этом используется следующая классическая модель.

Идеальный газ представляет собой совокупность хаотически движущихся по законам классической механики, упругих шариков, исчезающее малых размеров, взаимодействующих только в момент соударений между собой и со стенками сосуда.

Рассмотрим однородный газ, находящийся в изолированном неподвижном сосуде с непроницаемыми и гладкими стенками.

Молекулы (атомы) как упругие шарики движутся от столкновения до столкновения свободно со скоростью поступательного движения . Каждая молекула имеет свою скорость .

Очевидно, все макроскопические свойства такого газа, связанные со скоростью движения его молекул, будут определяться не индивидуальными скоростями каждой молекулы, а средней скоростью всех молекул газа . Но так как газ в целом, как механическая система, покоится, то .

Отлично от нуля среднее значение модуля скорости , а также квадрата скорости .

Величина называется средней квадратичной скоростью молекул газа (тепловой скоростью молекул газа) и определяется соотношением:

,

где N – число молекул газа.

Рассматриваемый газ находится в состоянии теплового равновесия и в целом неподвижен, откуда следует:

.

От столкновения до столкновения молекулы движутся свободно некоторое время . Среднее значение , вычисленное для всех молекул газа, называется средним временем свободного пробега .

За время молекула проходит путь . Среднее значение для всех молекул газа называется средней длиной свободного пробега . Таким образом, по истечении времени молекула в среднем претерпевает одно соударение. Длительность столкновения определяется размерами молекул (шариков). В принятой модели . Следовательно, молекулы идеального газа основное время проводят в состоянии свободного движения, не взаимодействуя друг с другом.

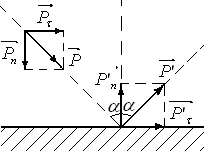Газ оказывает давление на стенки сосуда, механизм которого связан с процессом столкновения молекул газа с поверхностью сосуда. При столкновении упругих шариков с массивной гладкой поверхностью изменяется только нормальная к поверхности составляющая импульса (см. рисунок):

.

Поверхность при этом получает импульс в направлении нормали , где - масса молекулы (шарика).

Для упрощения схемы расчёта рассмотрим сосуд в форме куба со стороной (см. рисунок).

Найдём силу, действующую на заштрихованную грань, перпендикулярную оси Ox.

Импульс, полученный гранью при столкновении с молекулой, равен .

Так как промежуточными столкновениями можно пренебречь, учитывая эстафетный характер передачи импульса при упругом столкновении и малость времени соударения между молекулами (шарами), то для i-й молекулы время между двумя соседними столкновениями с выделенной гранью составит

,

то есть молекула за 1с столкнётся с выделенной гранью раз.

Таким образом, молекула за 1с передаёт выделенной грани импульс

.

Все N молекул газа передают за 1с импульс выделенной грани

.

Изменение импульса стенки в единицу времени – есть сила.

.

Учитывая, что

,

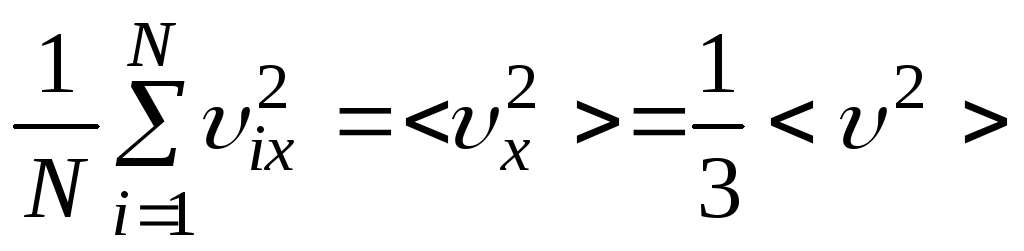получаем

.

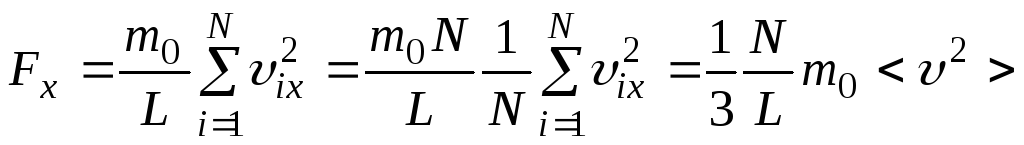Давление газа на выделенную грань равно:

,

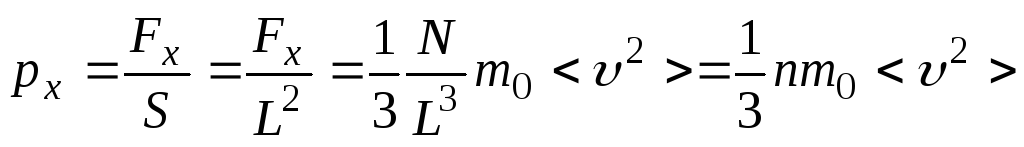где - концентрация молекул газа.

Правая часть полученного соотношения не зависит от индекса «x» и поэтому по аналогии можно записать: , где

.

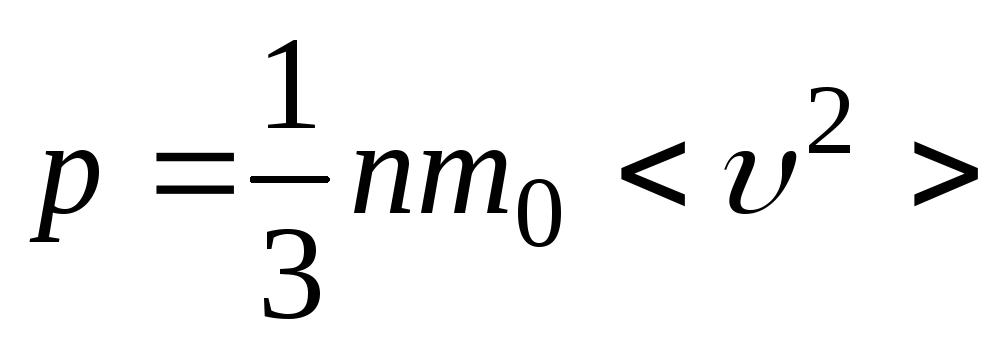Давление газа не зависит от направления, т.е. обладает свойством изотропии.

Полученное соотношение называется основным уравнением молекулярно-кинетической теории (МКТ) идеального газа. Оно связывает макрохарактеристику газа давление p с микрохарактеристиками молекул газа .

Отметим, что основное уравнение хорошо выполняется и для реальных газов, при невысоких давлениях, хотя молекулы последних и не являются упругими шариками, а их отражение от стенок сосуда в общем случае не подчиняется закону зеркального отражения и существенно зависит от свойств поверхности сосуда. Однако в равновесных условиях касательная составляющая импульсов отдельных молекул во всех случаях не даёт вклада в конечный результат, а нормальные составляющие (по закону сохранения импульса) определяют давление газа.

Основное уравнение МКТ идеального газа можно представить в более обобщённой форме через среднюю кинетическую энергию поступательного движения молекул газа:

.

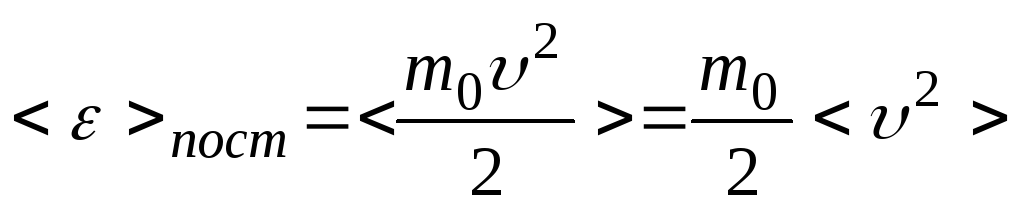Используя последнее соотношение для давления газа, находим:

.

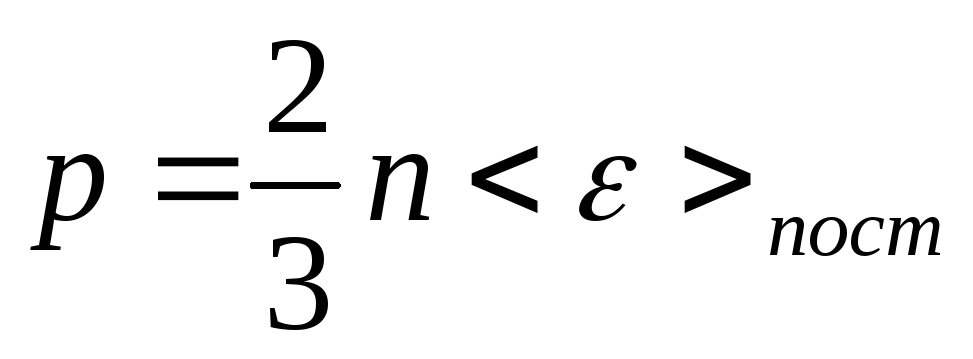В таком представлении основное уравнение применимо и для неоднородного газа, где , - концентрация молекул сорта, - средняя кинетическая энергия поступательного движения молекул неоднородного газа.

При этом общее давление неоднородного газа равно сумме

,

где 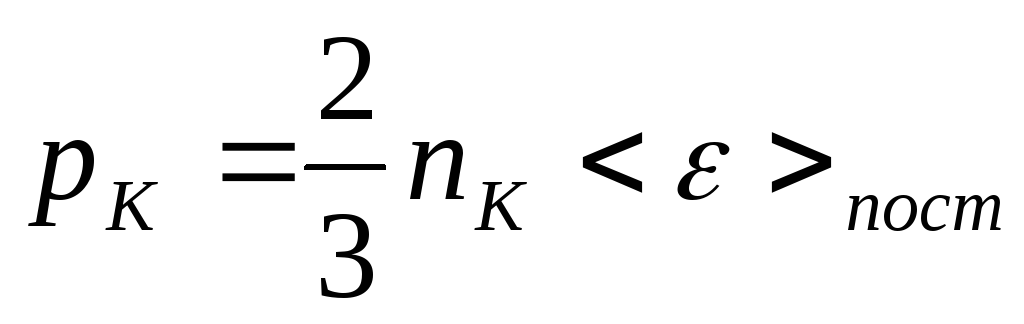- давление молекул сорта, называется парциальным давлением.

Последнее соотношение называется законом Дальтона в честь английского химика и физика, открывшего этот закон в 1801г.

Произведение равно плотности кинетической энергии поступательного движения молекул идеального газа .

Основное уравнение можно представить также в форме:

.

Лекция 10.