Элементы динамики твёрдого тела.

Твёрдое тело в общем случае обладает шестью степенями свободы. Из них три степени являются поступательными, связанными с движением центра массы, остальные три – вращательными, описывающими вращение твёрдого тела.

Произвольное движение тела может быть представлено совокупностью поступательного и вращательного движений. Таким образом, для описания движения твёрдого тела необходимо задать шесть скалярных уравнения или два векторных. Этими уравнениями являются:

,

,

где - радиус-вектор центра инерции тела,

- равнодействующая внешних сил, приложенная к центру инерции тела,

- собственный момент импульса тела,

- суммарный момент внешних сил относительно центра инерции тела.

В дальнейшем индекс «с» опустим.

Прежде чем переходить к рассмотрению различного вида движений твёрдого тела, остановимся на описании равновесия твёрдого тела. В состоянии равновесия твёрдое тело не должно перемещаться поступательно и не должно вращаться. Необходимым и достаточным условием равновесия твёрдого тела является равенство нулю:

,

,

где N – число внешних сил, приложенных к нему.

Замечание. Можно показать, что при записи моментов сил можно использовать не только центр инерции, но и любую точку пространства.

Закон сохранения момента импульса относительно оси.

Из основного закона динамики вращательного движения тела относительно оси при следует:

.

Момент импульса тела относительно оси сохраняется, т.е. внутренние силы не могут изменить момент импульса тела относительно оси вращения. Но внутренние силы могут приводить к пространственному перераспределению массы, т.е. изменять момент инерции тела относительно оси вращения.

Следовательно, для двух любых моментов времени должно выполняться равенство моментов импульса относительно оси вращения:

.

При уменьшении момента инерции возрастает угловая скорость вращения тела и наоборот.

Этим законом пользуются балерины, фигуристы, акробаты, гимнасты. Этим же законом можно объяснить конструктивные особенности вертолётов.

Мы уже отмечали фундаментальность закона сохранения момента импульса. Он одинаково применим к проблемам астрофизики и к проблемам элементарных частиц.

Кинетическая энергия вращения твёрдого тела.

К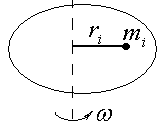инетическую энергию, связанную с вращением твёрдого тела относительно оси, можно представить как сумму кинетических энергий материальных точек твёрдого тела (см. рисунок).

.

Здесь учтено, что , - момент инерции тела относительно оси вращения.

Таким образом, для кинетической энергии вращения твёрдого тела имеем:

.

Отметим аналогию с выражением для кинетической энергии поступательного движения твёрдого тела:

.

Плоское движение твёрдого тела.

Как мы отмечали, в общем случае твёрдое тело совершает сложное движение, которое можно свести к совокупности независимых движений, связанных с движением центра инерции и вращением около центра инерции.

Относительно простым является плоское движение твёрдого тела. При этом движении пространственная ориентация оси вращения, проходящей через центр инерции, не изменяется с течением времени. Примером такого движения является скатывание круглого тела по наклонной плоскости.

Плоское движение твёрдого тела сводится к движению центра инерции, согласно уравнению:

и вращению относительно оси, проходящей через центр инерции, в соответствии с основным уравнением динамики вращательного движения:

.

Кинетическая энергия плоского движения твёрдого тела равна сумме кинетических энергий поступательного и вращательного движений:

,

где - скорость центра инерции, - угловая скорость вращения тела вокруг оси, проходящей через центр инерции.